ARIMA乘积季节模型在新疆猩红热发病预测中的应用
邹沛霖, 郑 强, 马 龙, 王 凯
(1新疆医科大学公共卫生学院, 乌鲁木齐 830011; 2新疆维吾尔自治区疾病预防控制中心, 乌鲁木齐 830000;3新疆医科大学医学工程技术学院, 乌鲁木齐 830011)
猩红热(scarlet fever)是一种常见的急性呼吸道传染病,多发于儿童和青少年,主要由空气飞沫传播,但目前尚无针对猩红热的疫苗[1]。2011年以来,全国报告的猩红热病例数明显上升[2],新疆地区亦呈高发趋势,本研究利用猩红热月发病例数建立ARIMA乘积季节预测模型,对新疆地区猩红热流行趋势进行预测,以期能掌握新疆地区猩红热发病规律和趋势,为早期发现暴发流行,及时采取防控措施提供参考依据。
1 资料和方法
1.1资料来源2006-2017年猩红热发病数据由“中国疾病预防控制信息系统”获得,主要为临床诊断病例。
1.2方法
1.2.1 ARIMA乘积季节模型 ARIMA乘积季节模型[3]是除季节滞后期自相关函数非零的模型以外,将季节模型和非季节模型相结合,既包括季节滞后自相关又包括低阶滞后自相关的简约模型。其公式简记为ARIMA(p,d,q)×(P,D,Q)S。其中p、d、q分别表示自回归阶数、差分阶数和移动平均阶数,P、D、Q分别表示季节自回归阶数、季节差分阶数、季节移动平均阶数,S表示周期步长。
1.2.2 ARIMA乘积季节模型建模步骤
1.2.2.1 序列白噪声检验 对原始序列执行白噪声测试,选用LB(Ljung-Box)统计量,若检验结果P<0.05,则序列不是白噪声,具有研究意义。
1.2.2.2 序列平稳性检验 对原始序列做平稳性检验,用单位根检验方法,若检验结果P<0.05,则序列平稳,若序列不平稳,一般采用差分或对数变换方法使序列平稳。
1.2.2.3 参数估计和模型诊断 确定拟合模型之后,利用极大似然法或最小二乘法来估计模型中未知参数的值。建立模型需要进行诊断,以确认模型在使用前是合理的,主要进行残差分析和参数的显著性检验。残差分析是看它提取的信息是否充分,即对残差序列进行白噪声检验,若残差序列为非白噪声,说明模型尚未完全提取序列信息,则需要替代模型来重新拟合序列。参数的显著性检验是测试参数是否与零显著不同,如果参数不重要,则影响不显著,并从模型中删除。
1.2.2.4 模型优化 能够有效的拟合序列波动的模型不止一个,因此要选择一个最佳拟合模型来对序列进行预测。所有的有效模型通过赤池信息量准则(AIC准则)和贝叶斯信息准则(BIC准则)进行优化。根据AIC、BIC函数值最小原则来综合确定最优模型。
1.2.2.5 模型预测 通过模型优化得到了最优模型,本研究把2006-2016年序列作为训练集,2017年序列作为验证集,用最优模型预测2017年序列,得到模型的拟合效果,可以用平均绝对百分比误差(MAPE)来判断[4],确定该模型是否适合该序列的预测,确定模型之后用于预测2018年序列。
1.3统计学处理使用Excel软件对数据进行整理和核对,采用R软件3.4.4进行统计学分析。序列是否平稳采用的是单位根(ADF)检验,白噪声检验采用LB统计量,检验水准α=0.05。
2 结果
2.1猩红热发病趋势分析从2006-2016年新疆地区猩红热月发病例数的序列图(图1)中可以看出,2006-2010年猩红热月发病数较低且较为稳定,2011年急剧增加,2011年12月发病数达到峰值,为560人,2012-2016年有明显的上升趋势,线性拟合曲线表明月发病例数整体呈上升趋势。对2006-2016年新疆地区猩红热月发病例数做因素分解,可以看出新疆地区猩红热月发病例数具有明显的趋势性和季节性变化(图2)。
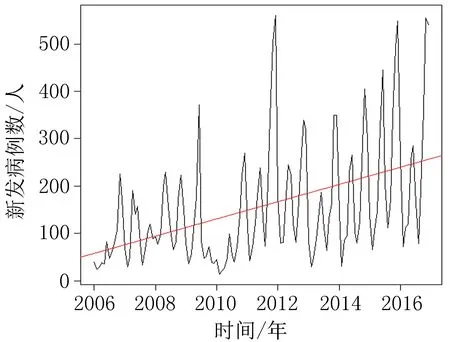
2.2原始序列检验对新疆地区2006-2016年猩红热月发病例的时间序列做纯随机性检验,检验结果P<0.001,表明此序列不是白噪声,具有研究价值。
2.3时间序列的平稳化处理通过图1看出此时间序列不平稳,又因该序列具有趋势性和季节性,故对序列做一阶差分和一阶季节性差分处理,处理后的序列如图3所示,处理后的序列做ADF测试,测试结果P=0.01,说明经过处理后的时间序列平稳。


2.4模型识别与建立ARIMA乘积季节模型的p,d,q和P,D,Q,S是待定的参数,原始序列经过一阶差分和一阶季节性差分转换为平稳序列,所以d和D取1,此序列的时间单位为月,所以S=12。故此乘积季节模型为ARIMA(p,1,q)(P,1,Q)12,对于剩下的4个待定参数,一般情况下不超过2阶,分别测试4个参数,p,q,P,Q分别取0,1,2的所有可能的模型,一共有81种待选模型。
2.5模型检验把81个待选模型逐一列举出来,然后对每一个候选模型的残差进行纯随机性测试,若测试结果P<0.05,说明此模型信息提取不够完整,舍弃该模型,若测试结果P>0.05,继续做参数显著性检验, 最后通过诊断的模型一共有15个。
2.6寻找最优的待选模型通过验证的15个模型中,模型ARIMA(1, 1, 1)( 0, 1, 1)12的AIC和SBC值均最小,为最优模型(表1)。模型残差的LB统计量的P值为0.863(P>0.05),模型的参数显著性检验结果表明模型的所有参数均显著非零(表2)。
2.7模型拟合与预测通过最优模型ARIMA(1,1,1)(0,1,1)12对2006-2016年新疆地区猩红热月发病例数进行拟合,结果如图4所示,从图中可看出,除2011年外,拟合的2006-2016年新疆地区猩红热月发病数与真实值基本相符,2011年拟合值较真实值浮动较大,其拟合值偏小于真实值,因为在2011年,猩红热发病数急剧增加,并达到2006-2016年猩红热月发病数峰值,原始时间序列在2011年变化比较迅速,因此拟合值有一些“滞后”,但总体来说拟合效果还是较为满意。计算得出此模型的MAPE为34.81,MAPE值稍偏大,因为原始数据的波动性比较大,因此MAPE值仍可接受。

表1 通过模型验证的AIC和SBC的值

表2 ARIMA(1, 1 ,1)( 0, 1, 1)12模型的参数检验

利用最优模型ARIMA(1,1,1)(0,1,1)12预测新疆地区2017年猩红热月发病例数,得到 2017年12个月的平均相对误差为20.7%,按全年发病数计,相对误差仅为3.0%,MAPE值为20.52,表明此模型预测效果较好(表4)。通过模型ARIMA(1,1,1)(0,1,1)12预测新疆地区2018年猩红热月发病例数,结果显示2018年新疆地区猩红热月发病数可能仍处于较高水平,预测得到新疆地区2018全年一共可能有3 474例猩红热新发病人,其中月新发病数最大可能出现在11月,新发病例数可能为556例(表5)。
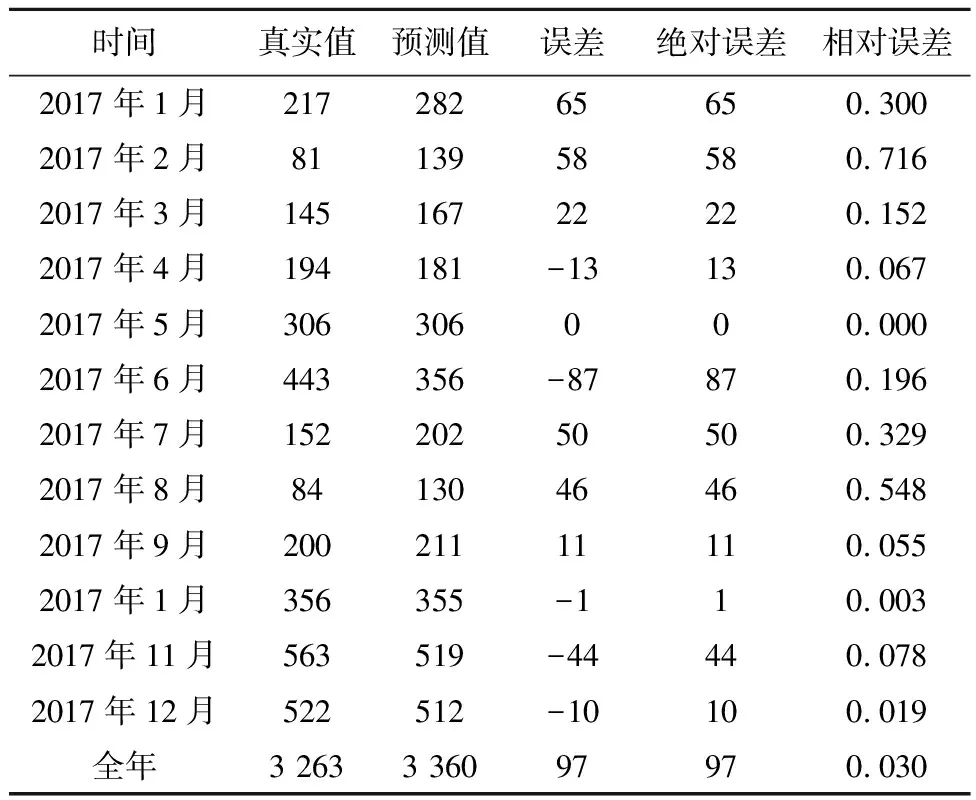
表4 2017年猩红热月新发病数预测值与实际值比较
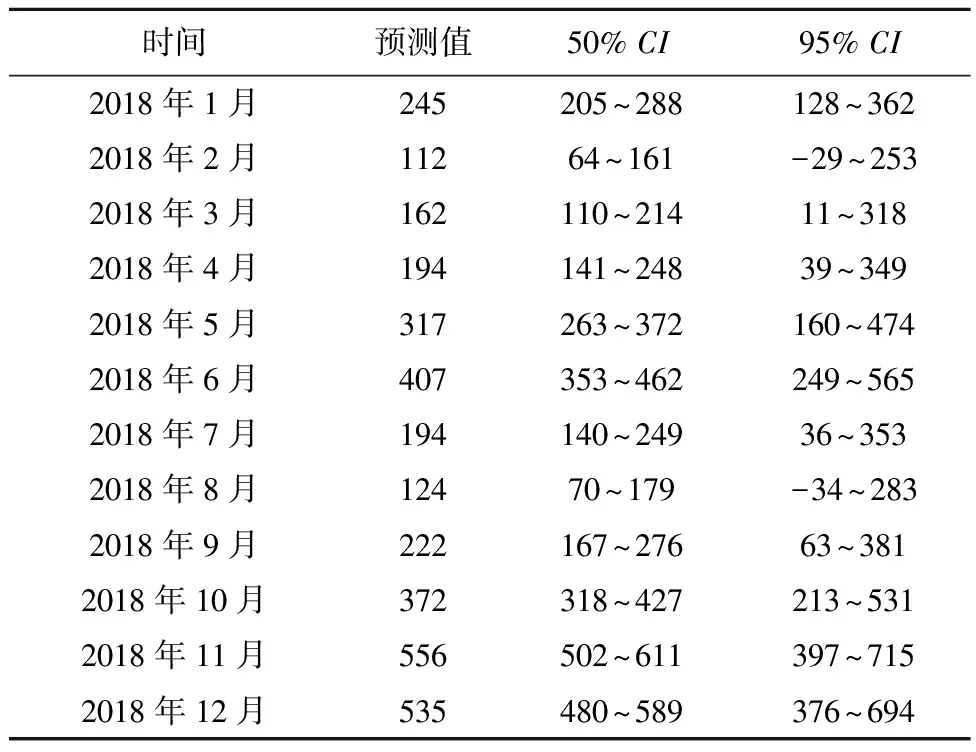
表5 ARIMA(1,1,1)(0,1,1)12模型预测2018年猩红热月新发病例数
3 讨论
猩红热在20世纪初以前,曾是主要的死亡原因之一,随着抗生素的广泛使用,猩红热的发病率显著降低,但是近10年的研究显示,该病在我国香港、韩国和英国再次流行[5-8]。2011年以来,全国报告的猩红热病例数急剧上升,2004-2010年的年均发病率为1.910 5/10万,2011-2016年为4.012 5/10万,2011-2016年的年均发病率约是2004-2010年的2.1倍[2]。从新疆统计年鉴可以得到,新疆地区2004-2010年的年均发病率为5.172 3/10万,2011-2016年的年均发病率为10.870 6/10万,新疆地区2011-2016年期间的年平均发病率约是2004-2010年期间报告的2.1倍。其中2015年发病率为达到历年最高,达到13.54/10万。且2015-2016年发病率均超过12/10万。针对这种情况,应加强对猩红热的防控工作,而目前没有针对于猩红热的疫苗,因此对于传染源的管理尤为重要,猩红热的发病人群主要集中在儿童和青少年,卫生部门和教育部门应加强对学校和幼托机构的疫情管理,做好卫生健康教育宣传工作。
猩红热的发病具有一定的季节性,而ARIMA乘积季节模型是除季节滞后期自相关函数非零的模型以外,将季节模型和非季节模型相结合,既包括季节滞后自相关又包括低阶滞后自相关的简约模型,ARIMA模型建模对于时间序列有一定的要求,数据量最好要达到60个[9]。本研究对新疆地区2006-2016年猩红热的月发病例数进行拟合,共收集了144个数据,通过不断的拟合,最后得到最优模型为ARIMA(1,1,1)(0,1,1)12,此模型拟合值和实际值十分相近,2017年的预测值和实际值基本一致,表明此模型可以较好地拟合并预测新疆地区猩红热流行趋势,为控制新疆地区猩红热疫情提供依据。ARIMA模型是一种比较传统的预测方法,仅根据月发病数来拟合模型,有一定的局限性,环境的改变很容易导致预测效果不理想,ARIMA模型对于短期预测时精度较高,长期预测精度会下降,因此预测结果与当年实际发病情况是否一致,须做进一步评估。

