例谈高考数学创新型试题的特点*

☉四川省内江师范学院数学与信息科学学院 赵思林

☉四川省内江师范学院数学与信息科学学院 纪定春

☉四 川 省 资 阳 市 教 科 所 卢勇刚

2009年5月，《数学通报》发表了《高考数学创新型试题的几个特点》一文，文章重点介绍了高考数学创新型试题的特点，即立意的鲜明性、背景的深刻性、情境的新颖性、设问的灵活性［1］.近10年以来的高考数学创新型试题仍体现了这些特点.但也有一些新的变化，一是增加了数学文化，这体现了新课改对数学文化的强化；二是增加了条件（结论）的开放性试题；三是10年前以分省命题为主又变为以教育部命题中心命题为主；四是国家提出了“三个第一”，即“发展是第一要务，创新是第一动力，人才是第一资源”，对教育来讲，“创新”和“人才”占了“两个第一”，这无疑对培养和选拔创新人才提出了新的要求.

一、立意的鲜明性

立意是指高考试题考查的目的［1］.高考命题一般以立意为中心.自1999年起，高考命题就强调“能力立意”，“能力立意”就是首先确定考查能力的内容和类型，然后根据考查能力的层次（了解、理解、掌握等）的具体要求来确定所要考查的知识内容，最后设计出符合知识要求和能力要求的试题.高考数学简单地讲，主要是四考：考基础知识，考思想方法，考能力素养，考数学意识（应用意识和创新意识）.高考数学创新型试题是根据能力素养来立意命题的指导思想，并用来衡量考生的发展性和创造性的新颖试题［1-2］.以能力素养来立意的数学试题一般以数学基础知识、基本技能和数学思想方法为载体，以考查基础知识、基本运算和基本方法为主要形式.

1.考查基础知识的灵活应用

数学基础知识和基本技能是形成和发展数学能力素养的必要基础，是领悟数学基本思想的重要载体.高考对基础知识的考查不是知识的机械记忆和简单模仿，而是侧重于考查对基本概念的理解及基本思想方法的运用.考查基础知识的试题一般都含有教材背景，但解答这类试题所用到的思想方法和能力素养又略高于教材，因此这类试题既体现了基础性又有一定的综合性.

例1（2017年全国卷Ⅲ理科第17题）△ABC的内角A，B，C的对边分别为a，b，c，已知sinA+cosA=0，a=，b=2.

（1）求c的值；

（2）设D为BC边上一点，且AD⊥AC，求△ABD的面积.

评注：本题考查了辅助角公式、正弦定理、余弦定理、勾股定理、面积公式等基础知识，是一道考查基础知识点的灵活运用和综合应用的好题，该题既源于教材又高于教材.

2.考查数学思想方法

数学思想方法是数学中最有价值的核心素养，历来都是高考立意的基本原则．

例2（2017年全国卷Ⅰ理科第21题）已知函数f（x）=ae2x+（a-2）ex-x．

（1）讨论f（x）的单调性；

（2）若f（x）有两个零点，求a的取值范围．

分析：问题（1）考查了含参变量函数的单调性问题，主要涉及分类讨论及单调性的判定．当a≤0时，可知函数f（x）在R上单调递减，当a>0时，有f′（x）=2ae2x+（a-2）ex-1，令f′（x）=0，可得x=-lna，故可得f（x）在（-∞，-lna）上单调递减，f（x）在（-lna，+∞）上单调递增．

问题（2）是对问题（1）中函数最值的深入考查，通过问题（1）可知，当a≤0时，函数f（x）在R上单调递减，故函数f（x）至多有一个零点，与题设不符.则只能当a>0时，f（x）有两个零点．要使函数f（x）有两个零点，结合f（x）先单调递减后单调递增，等价于函数的最小值小于零．故f（-lna）<0，即a-1+alna<0，则a<1，综上可得a∈（0，1）．

评注：本题考查了含参变量函数的单调性、复合函数求导法则、参数讨论、函数最值、函数零点等基础知识，涉及转化与化归、分类讨论、数形结合等数学思想，集中体现了高考对数学思想方法的考查．

3.考查应用意识和创新意识

应用型试题是考查考生“综合实力”的试题，是考查学生数学综合能力和素养的好题型［1］．“考查应用意识”也是命题组长期坚持的命题方针，其中应用意识表现在数学建模、用数学知识分析和解决实际问题等方面．试卷既突出概率与统计的应用性，也重视函数（含数列）、三角等知识的实际应用．应用性试题、探究性试题、开放性试题是创新型试题的基本题型，担负着考查创新意识的重任．面对应用性试题、探究性试题、开放性试题等创新型试题时最好的办法就是组织学生适当地开展研究性学习［1］，有意识地让学生在学习的过程中经历数学探究的整个过程，并且在这个过程中教师要积极地调动学生的主动性，激发学生对数学探究的兴趣，引导学生独立自主地观察数学现象，收集与整理数学材料，提出、分析并解决数学问题，探究数学规律，猜想数学命题，制定解题方案，回顾心路历程，提炼数学思想方法等．

例3（2017年上海卷第19题）根据预测，某地第n（n∈N*）个月共享单车的投放量和损失量分别为an和bn（单位：辆），其中，第n 个月底共享单车的保有量是前n个月的累计投放量与累计损失量的差．

（1）求该地区第4个月底共享单车保有量.

（2）已知该地共享单车停放点第n个月底单车容纳量为Sn=-4（n-46）2+8800（单位：辆）．设在某月底，共享单车的保有量达到最大，问：该保有量是否超出了此时停放点的单车容纳量？

分析：对于问题（1），首先明确共享单车保有量是累计投放量与累计损失量之差，然后将n=1，2，3，4代入an，bn，算出前4个月累计投放量之和与累计损失量，差值即为保有量，即（a1+a2+a3+a4）-（b1+b2+b3+b4）=965-30=935.

对于问题（2），由题意可知，当投放量大于损失量时，共享单车保有量增加，根据an和bn列出不等式，求出n的最大值为42，再算出当n=42时的最大保有量8782辆，同时算出当n=42时的最大容纳量8736辆，最后比较最大保有量与最大容纳量的大小，即8782>8736，所以，此时保有量超过了容纳量.

评注：本题背景鲜活，具有生活气息，还是人们所关注的热点话题．命题者用社会热点作为切入点，将其与日常生活中共享单车的投放和损失联系起来，巧妙设问，主要考查学生的社会生活经验、阅读理解能力、分段函数值的求解，保有量、投放量和损失量之间的关系，以及投放量与实际环境容纳量等，考查了学生的数学理解能力、逻辑运算能力及数学综合素养等．通过理解各要素之间的数量关系，然后进行逻辑运算，进而可以对问题作出迅速、准确的解答．

二、背景的深刻性

1.高等数学背景

高考命题专家多以非常熟悉高等数学的大学教授为主，他们善于用高等数学知识为背景设计创新型试题，因为高等数学中的思想方法、思维方式对进一步的学习极为有用．因此研究高考试题的高等数学背景对提高高中数学教学质量和复习应考水平是有益的．

例4（2017年全国卷Ⅲ理科第21题）已知函数f（x）=x-1-alnx．

（1）若f（x）≥0，求a的值；

分析：对于问题（1），先根据重要不等式lnx≤x-1在x>0时恒成立，可以“猜测”出a=1，然后进行严格的证明．

思路1：导数法.可以直接利用求导找到函数f（x）的极值点，然后根据条件找出f（x）的最小值，最后使得最小值非负，即可求出a的值．

评注：问题（1）考查含参数不等式恒成立问题，命题以重要不等式lnx≤x-1为背景，在具体求解方法上，又具有灵活多样的特点，若直接使用导数求解，解题思路不失一般性，但过程较为烦琐，如直接使用法1或法2即可简洁获解；问题（2）是在问题（1）的基础上深入考查lnx≤x-1的性质、对数运算的性质、等比数列求和等，属于横向知识的大“融合”，是考查考生的数学素质和综合能力素养的好题目，具有一定的挑战性和区分度．值得注意的是，在平常的教学中也可以结合考题的高等数学背景，适当地补充高等数学知识，切不可过多补充，以免增加学生的学习负担和压力．

以高等数学知识为背景的试题很多．常见的有拉格朗日中值定理、柯西中值定理（2015年全国卷理科第15题和2016年四川卷理科第21题都有柯西、拉格朗日中值定理背景）、柯西不等式（2012年四川卷理科第12题，2017年全国卷Ⅱ理科第23题）、洛必达法则（2016年新课标卷Ⅰ数学第21题）、函数凹凸性（2012年福建卷理科第12题、2018年全国卷Ⅲ理科第21题）、零点存在定理（2012年陕西卷理科第21题、2017年全国卷Ⅰ理科第21题）、麦克劳林展开式（2008年全国卷Ⅱ理科第22题、2018年全国卷Ⅲ理科第21题）、重要不等式（2016年全国卷文科第21题）等，这些命题背景都值得注意．

2.数学文化背景

例5（2018年全国卷Ⅰ理科第10题）图1来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形ABC的斜边BC，直角边AB，AC，△ABC的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ，在整个图形中任意取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别为记为p1，p2，p3，则（ ）．

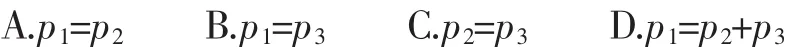
图1

分析：可以设出直角三角形的三边长度，然后根据三角形和圆的面积公式依次计算出各自的面积即可，解答过程略．最后结果为A．

评注：该题目以“古希腊数学家”研究的几何图形为背景，结合高中的概率进行考查．考题情境十分新颖，颇有数学文化气息，对考生的数学文化具有熏陶作用．本题考查学生的创新意识、观察分析能力、逻辑运算能力等，也充分体现了新课改中数学文化渗透的重要性．

三、情境的新颖性

数学情境是数学问题的载体，是实现命题立意的中介系统．数学问题是数学考试的基本形式，也是数学考查的重要手段．情境的新颖性是创新型数学试题的共同特征［1］，体现了高考的公平、公正．考生面对情境新颖的试题时，一般需要具备阅读理解能力、信息筛选能力、问题分析能力、问题探究能力和问题解决能力．

例6（2017年全国卷Ⅰ理科第16题）如图2，圆形纸片的圆心为O，半径为5cm，该纸片上的等边三角形ABC的中心为O．D、E、F为圆O上的点，△DBC，△ECA，△FAB分别是以BC，CA，AB为底边的等腰三角形．沿虚线剪开后，分别以BC，CA，AB为折痕折起△DBC，△ECA，△FAB，使得D、E、F重合，得到三棱锥．当△ABC的边长变化时，所得三棱锥体积（单位：cm3）的最大值为______．

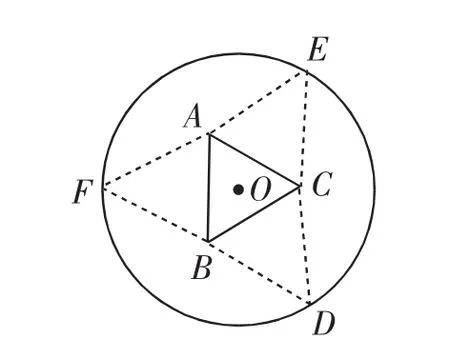
图2

分析：对于圆中动态变化的三角形围成的三棱锥的体积最大值问题，平时在练习中较为少（罕）见，在初次接触此题时，没有现成的公式和公理可以直接套用．但注意到围成三棱锥的四个三角形都是较为特殊的三角形，那么可以通过圆的半径来引入未知量，然后借助其中的等量关系，表示出三棱锥的体积，最后可以通过导数或者均值不等式来解决．

评注：本题情境新颖、背景深刻、设计独特，具有很强的抽象性和综合性．从试题的情境来看，本题以三角形的重心、三角形的高、折叠前后的不变性、勾股定理、三棱锥的体积、函数最值等多个知识点为素材，经过精心的打磨和包装，以求解（动态）最值的形式呈现出来，此类型试题在常规的参考书籍中较难见到，给了考生一个全新的问题情境，该试题具有较强的横向知识融合性，又考查学生阅读理解能力、隐含条件（关系）挖掘能力、数学综合素养能力等．这类以综合性知识为背景的创新型问题，能有效考查学生的学习潜质，其已成为高考数学试题的亮点和热点，值得关注．该题目是一道很好的创新型试题，对该类型试题的解决可以按照“情境提取信息—综合分析信息—选择适当的数学工具—转化问题—问题获解”的步骤进行．

此外，情境新颖性问题还有很多．如高等数学的概念、新定义性问题、归纳猜想问题、合情推理问题等，都可以增加试题的情境新颖性．如：2008年福建卷理科第16题数域的概念与性质；2012年福建卷文科第9题和理科第7题和2015年湖北卷理科第6题以特殊函数（狄利克雷函数、符号函数）为素材；2014年山东卷理科第15题，新定义“对称函数”；2016年上海卷理科第23题，“无穷数列”；2016年四川卷理科第15题，新定义“伴随点”；2016年北京卷理科第20题，新定义“G时刻”与数列结合；2015年山东卷理科第11题，考查归纳猜理；2018年江苏卷第19题，考查新定义“S点”等，这些都属于情境新颖性试题，值得仔细品味．

四、设问的灵活性

设问是试题表现的具体形式，是需要解决和回答的目标问题．高考解答题从设问的数量来看，一般为两问或三问．从各个小题的关系上来看，问与问之间相互衔接，存在逻辑关系，有时表现为上问为下问起铺垫作用，后问是对前问的深化和拓展.灵活的问题设计往往蕴含了命题者深刻的命题意蕴，值得思考与体会．

例7（2015年江苏卷第20题）设a1，a2，a3，a4是各项为正数且公差为d（d≠0）的等差数列．

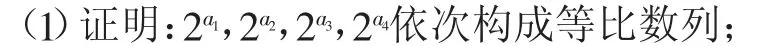
（2）是否存在a1，d，使得a1，a22，a33，a44依次构成等比数列？并说明理由；

（3）是否存在a1，d及正整数n，k，使得a1n，a2n+k，a3n+2k，a4n+3k依次构成等比数列？并说明理由．

评注：本题将等差数列与等比数列结合在一起，用巧妙而灵活的设问，使问题与问题之间层层推进，步步深入．本题综合考查了等差数列和等比数列的定义与性质，属于纵向深入考查型试题，具有挑战性和区分度．本题考查了数学探究能力、数学推理能力、逻辑运算能力等数学核心素养能力，同时考查了代数与方程、转化与化归等思想．问题（1）为常规的等差数列与等比数列综合型试题，若将指数2换成任意常数或参数m，可以加大辨别难度．问题（2）和问题（3）可以运用反证法，利用等比数列的性质和题设条件推出矛盾．这是高考数列性质深入考查的好题之一，值得研究和品味．

高考数学创新型试题既要考查知识点的横向交汇性，又要考查具体知识点的纵向深刻性，它是集知识、方法、思想、能力于一体的新颖性问题．在创新型试题备考的过程中，要有意识地强化对学生创新意识和创新能力的培养，适当开展一些研究性学习，让学生对创新型试题的特点有明确的认识，把握其命题的规律和试题的特征．这样不仅能够培养学生解答创新型试题的能力和素养，而且有利于学生后续的学习和发展．