中国中产阶层比重的测度及变迁研究

张晓华，纪 宏

（1.首都经济贸易大学 统计学院，北京 100070；2.郑州大学西亚斯国际学院 商学院，郑州 450000）

0 引言

中国社会要发展成为一个可持续发展的、稳定的“橄榄型”现代社会,需要培育庞大的社会中间力量，这个中间力量即中产阶层，然而，中产阶层规模有多大？发展现状到底如何？变化趋势怎样？这一系列问题都值得研究。国内外学者对中产阶层已经有了比较全面深入的研究，经济学界常从收入指标入手，社会学界常辅助问卷调查数据从多指标研究中产阶层。本文将在前人学者的研究基础上综合宏观、微观数据对以恩格尔系数单个指标界定的中产阶层的现状进行描述性统计分析，并对其比重进行测度，最后研究中产阶层的变迁趋势，从而找出中产阶层发展的规律，对于完善中产阶层的研究，稳定社会、实现共同富裕、全面建设小康社会具有重要的意义。

1 概念的界定和数据说明

1.1 中产阶层概念的界定

通过对国外相关文献的研究发现，国外一般将中产阶级、中间阶层和中产阶层等概念与中等收入群体的概念等同，普遍使用Middle Class。国内学者对“中产”概念进行界定时有两种方式，一种是回避对“中产”概念的明确界定；另一种是对“中产”做一个描述性的分类说明。但所有学者都认为“中产”与职业关系密切，且大多以收入、财产或消费指标来定义中产。本文认为概念的界定首先要服从研究者的目的且能做定量分析，其次要充分考虑概念赖以存在的基本理论基础和社会现实基础，最后，鉴于收入可能会受到概念界定的不统一、调查难度、地域收入消费水平的差异、经济周期，“财不露富”的心理作用、被调查者回答的模糊和避讳、地下经济和隐形收入的存在等多种因素的影响,因此，本文选择较容易准确测定的消费指标来界定中产阶层，且消费方式能够更加系统地体现出一个人的生活习惯及生活品质。

消费指标中常用的是恩格尔系数，考虑到中国还处于社会转型阶段，加上居民自身的生活习惯、经济制度和保障等因素，本文将恩格尔系数进行修正以界定中产阶层的标准。本文选择将国际标准的恩格尔系数减去0.1，即恩格尔系数在0.3～0.4之间来界定出我国的中产阶层。

1.2 数据说明

本文的数据从两方面来考虑，一是采用宏观层面中国统计年鉴上的数据，包括城镇、农村、七分组或五分组数据。二是采用微观层面中国综合社会调查（Chinese General Social Survey，CGSS）已公布的最新数据，包括2015年社会综合调查数据和2010年社会综合调查数据（恩格尔系数的数据在CGSS数据中仅这两年有统计），且由于学生人口自身职业、收入乃至消费行为的不确定性，很难作为划分中产阶层的有力依据,因此，本文选取CGSS综合社会调查中16～70岁的非学生群体这一部分具有统计分析价值的适龄社会人口的样本数据。有效问卷数分别为8250例（2015年）和10510例（2010年）。

2 中产阶层的现状分析

2018年1月，国家统计局局长宁吉喆指出，我国消费结构中有一个很重要的变化是恩格尔系数从2016年的30.1%降到2017年的29.3%，说明居民生活水平大幅提高。考虑近几年我国恩格尔系数，无论是全国还是城市、农村，恩格尔系数都在30%～40%之间，若这样认为我国全民属于恩格尔系数界定的中产阶层，显然也不太合理，但是否能从某些方面认为中产阶层比重在扩大。

综合2015年微观CGSS调查数据来看（见下页表1），2014年我国适龄社会人口的恩格尔系数在30%～40%之间，已经达到了小康水平。中位数的值低于平均值，说明社会消费构成右偏，标准差低于平均值且其自身数值也很小，说明数据离散程度低，恩格尔系数较为集中，消费行为相似。按照本文中产阶层的界定标准，我国消费中产的比重达到了18.22%，相较于2009年的17.97%，恩格尔系数和中产阶层的比重都略有增加。由于消费水平存在地区差异，进一步按照发达地区、较发达地区和欠发达地区三个区域来统计恩格尔系数，可以看出，2014年发达地区均值降低，且中产阶层比重显著降低，说明发达地区生活质量更好，贫富差距拉大，欠发达地区恩格尔系数均值显著降低，中产阶层比重增加，说明欠发达地区居民生活水平得到改善。

表1 恩格尔系数统计表 （单位：%）

3 中产阶层比重的测度

首先构造衡量中产阶层的恩格尔系数的密度函数，其次用核密度函数对其进行估计，得到恩格尔系数的核密度函数，然后界定衡量中产阶层的恩格尔系数的上下限0.3～0.4，最后对核密度函数做数值积分求出中产阶层的比重。

3.1 测度模型

核密度估计是用来估计未知密度函数的一种方法，属于现代非参数检验方法之一。若f（x）是一维总体的密度函数，设K（·）是R上一个给定的Borel可测函数,hn＞0是一个与n有关的常数，满足，定义：

但式（12）中有未知量f（x），本文采用 Sliverman（1986）提出的经验法则，即假定f（x）为正态密度函数N（0,σ2），选取高斯核，则最优带宽为：

最终，一维度核密度函数为：

3.2 中产阶层的比重

根据2015CGSS和2010CGSS数据计算出2014年和2009年的恩格尔系数，用R软件画出其核密度图1。从图1中可以看出我国多数人群恩格尔系数在0.3左右。核密度图也呈现略微右偏的形状，说明食物消费支出大的人群比重相对较小，人们生活水平差异大。2014年相较2009年核密度曲线表现出以下特点：曲线向右略微平移，说明居民的食物支出水平提升，家庭生活水平略微降低；曲线峰值略高，顶部上升，宽度略微减小，说明收入恩格尔系数差距缩小，中产阶层比重略微增加。进一步地类似于上面的方法用R软件画出2014年、2009年城镇、农村这两年的家庭总收入核密度图以及2014年和2009年发达地区、较发达地区和欠发达地区的家庭总收入核密度图，得到的结论是：2014年城镇家庭恩格尔系数相较于2009年位置变化不大，农村家庭恩格尔系数明显右侧移动，说明农村家庭生活水平质量下降。发达地区核密度图2014年较2009年宽度变宽，较发达地区变化基本不变，欠发达地区整体右侧移动，说明发达地区生活水平质量拉大，较发达地区基本没有变化，欠发达地区人们生活水平变差。

图1 2009年、2014年家庭恩格尔系数

结合上文给出的消费界定的中产阶层的上下限标准，即恩格尔系数在0.3～0.4之间，可以得到中产阶层的比重如表2所示。可以看出，2014年较2009年全国中产阶层比重略微增加，城市中产阶层比重略微减少，发达地区中产阶层的比重也有降低。其原因或许跟经济增长、收入变化的变动有关，也跟城市、发达地区人们有住房、消费等较大压力有关。

表2 中产阶层的比重 （单位：%）

4 中产阶层的变迁分析

函数型数据的分析方法是将每一个样本观测看成是一个整体来考虑，且在经济函数型数据分析中，学者们常需要找感兴趣的变量随时间变化的主要变异方式，同时又想知道多少个这样的变化方式或形态可以较好地拟合原始曲线样本，即需要通过确定曲线数据的典型函数特征探讨数据变异的主要成分。主成分分析就能很好地解决这种问题，本文要研究恩格尔系数构成的中产阶层的变化规律，从时间上去看中产阶层的变迁趋势，所以把函数型数据主成分法引入到此。且由于微观数据的不充分（只有两年的数据），不足以表示近几年中产阶层的变迁情况，本文采用国家统计局公布的城镇七分组数据和农村五分组数据将函数型数据的基展开和函数型主成分分析的方法引入中产阶层的变迁分析之中。

4.1 函数型数据的基展开

本文采用B样条基将离散的数据转化为函数。假定基函数f（xi）是样条函数，一个有k个结点的三次样条函数可以由b1（x1）,b2（x2）,b3（x3），…，bk+3（xi）的线性组合构成，其中，bi（xi）有多种选法，本文选用三次多项式为基础，然后在每个结点添加一个截断幂基，即：

其中，h（x,ξ）=（x-ξ）3,（x＞ξ），h（x,ξ）=0,（x＜ξ）。ξ是结点，估计模型时,采用最小二乘法估计k+4个系数。

4.2 函数型主成分分析

4.2.1 函数型主成分的数学模型

经典的多元统计分析中是要找特征向量。在函数性数据主成分分析中，这个特征向量是一个变动的函数，叫主成分权函数，记为ξ（s），其中s在一个区间T中变化，且ξ（s）平方可积。

第j个函数主成分，其权函数ξj（s）满足如下数学模型的条件：

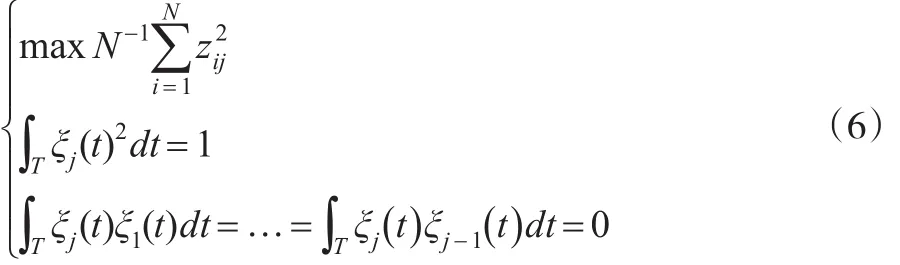
其中，zij= ∫Tξj（t）xi（t）dt为第i个样品的第j主成分得分，i=1,2,…,N。且求得的诸多权函数ξj（s）满足标准正交约束条件，即：

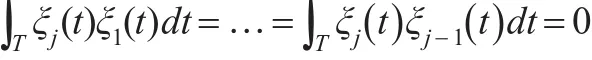
本文将这K个正交的权函数ξk（s），k=1,2,…,K，作为基函数。

4.2.2 函数型主成分的求解方法

在多元统计分析中，求解主成分是要寻求协方差阵或相关系数阵的特征值和特征向量。在函数型主成分分析中是要求解Vξ=ρξ这个特征方程和和对应的特征函数。

（1）求解特征方程

若令p×p阶矩阵V=N-1X"X，即V表示样本方差—协差阵，类似于多元统计分析，求解函数性主成分权函数ξj（s）转化为解如下的特征方程：其 中 ，设xi（s）和xi（t）的 协 方 差 函 数 为ν（ ）s，t，s，t∈T，即：

若定义一个算子：

即V是权函数ξ的一个积分变换，并称其为协方差算子。因此式（7）的特征方程式可表述为Vξ=ρξ（注意这里的ξ是特征函数，不是特征向量）。

（2）离散化法求解权函数

设观测xi（t）的时点t1，t2，…，tn均等地分布于区间T，即在区间T的n等分点上取值，这样可得到多元数据集X：

类似多元统计分析，可求出满足式（11）的特征值和特征向量：

其中，u为n维向量。

样本方差-协差矩阵V=N-1X"X的元素为ν（tjl,tk）。对于给定的函数ξ，令ξ͂是由ξ（tj）构成的n维列向量，l是区间T的长度，w=l/n。于是，对于任意的tj有：

因此，函数性特征方程Vξ=ρξ有近似离散形式：

这个方程的解将对应于Vξ=ρξ式的解，特征值之间的关系ρ=wλ。标准化约束的近似离散形式是因此如果向量u是矩阵V的标准化特征向量，则ξ͂=w-1/2u。在得到ξ͂后，使用任何简便的插值法便可从离散值ξ͂获得近似特征函数ξ。

4.3 中产阶层变迁的数据分析

由于2013年前后数据口径有很大的变化，且城镇七分组数据和农村五分组数据只在2013年前统计，因此本文采用的数据是《统计年鉴（2002—2013）》中计算出的恩格尔系数进行中产阶层变迁的分析。

4.3.1 恩格尔系数分组数据基展开

本文采用R软件选取B-样条基展开，将七分组城镇恩格尔系数数据及其变动率绘制修匀曲线。结论是：除最低收入组的恩格尔系数的波动相对大点外，其他六组恩格尔系数虽一直有小幅波动，但总体上保持平稳的发展。衡量中产阶层群体的中间三条曲线（中下组、中等组和中上组）的恩格尔系数变动率波动特征一致，都是周期性的先增后减，且在2004年、2008年恩格尔系数达到增幅最大，2012年后有下降的趋势。同样的，根据五分组农村恩格尔系数和其变动率也做B-样条修匀处理，结论是：农村五分组曲线比城镇七分组曲线变动剧烈，并且整体波动趋势下降。在2004年达到最高点，原因可能是2004年物价飞涨，但收入并没有相应的增加，且中间三条曲线即衡量中产阶层的群体自2012年后有下降的趋势，说明农村中产阶层人群近几年来生活水平在提高。但从农村恩格尔系数变动率五分组数据来看，除低收入组变动率在接近2012年变动异常低外，其他组波动率基本一致。

4.3.2 恩格尔系数分组数据函数性主成分分析

进一步地，采用R软件分别做七分组城镇恩格尔系数变动率和五分组农村恩格尔系数变动率的主成分偏离均值的效果图。从图2和图3可以看出，无论是城镇恩格尔系数还是农村恩格尔系数都是第一主成分偏离均值较多，波动较大，并且解释了函数的大部分变动。并且第一主成分都是2006年以前和2010年后导致五分组恩格尔系数大幅变动。事实上，2006年、2010年国家一系列惠民政策的出台，增加了人们的收入，相应的增加了消费支出，因此在各项政策的管控下，五分组恩格尔系数产生了变动。

图2七分组城镇恩格尔系数变动率的主成分偏离均值的效果图

图3五分组农村恩格尔系数变动率的主成分偏离均值的效果图

5 结论

恩格尔系数界定的中产阶层群体密度函数略微呈现右偏分布，说明人们生活水平差异明显。2014年相较2009年，人们生活水平质量下降，但差异缩小。从城乡来看，城镇恩格尔系数变化不大，农村右移明显，说明农村生活质量下降。从地区来看，说明发达地区生活水平质量拉大，较发达地区基本没有变化，欠发达地区人们生活水平变差。总体来说，中国中产阶层比重规模不大，但整体有增加的趋势。

函数型数据分析的结果显示：中产阶层群体恩格尔系数曲线波动特征一致，都是周期性的先增后减，且2012年后有下降的趋势，说明各收入组人们的食物支出在减少，生活水平有提高。城镇恩格尔系数波动率的修匀曲线波动大致相同，但农村恩格尔系数曲线相较城镇变动剧烈，从恩格尔系数主成分偏离均值的效果图可以看出，无论是城镇还是农村都是2006年以前和2010年后导致恩格尔系数大幅变动。

总之，我国中产阶层虽然比重大致都在增加，但规模不大，与欧美等发达国家中产阶层的比重相比仍有较大差距，但人们生活质量确实得到提高，因此“扩中”的任务仍很艰巨。