你若不离不弃 我必生死相依

周 斌

“你若不离不弃，我必生死相依”表明两人关系亲密或对爱情忠贞。而我们的初中数学中，也有这样一对小伙伴——方程和不等式，它们是生死相依的关系。今天我们就来说说它们的亲密关系。

考点一：方程和不等式的基础知识

例1（2018·江苏扬州）关于x的方程mx2-2x+3=0有两个不相等的实数根，那么m的取值范围是_______。

【分析】本题主要考查两点：1.既然题目中提出方程“有两个不相等的实数根”，暗示了这个方程必须是一元二次方程，即二次项系数不为0；2.要会判断一元二次方程的根的情况。

解：关于x的方程mx2-2x+3=0有两个不相等的实数根，

∴m≠0，且Δ=（-2）2-4×m×3=4-12m＞0，

【点评】解决此题的关键是理解题目中的“关于x的方程mx2-2x+3=0有两个不相等的实数根”的本质：首先二次项的系数不为0；其次根的判别式要大于0。

例2（2017·江苏宿迁14题变式）若关于x的分式方程-3解是非负数，则实数m的取值范围是_______。

【分析】本题主要考查分式方程的解法、分式方程增根的意义等知识，要求同学们能用不等式（组）来刻画分式方程解的情况。

解：原关于x的分式方程可变形为

方程两边同乘最简公分母（x-2），得m=-（1-x）-3（x-2），

∴x≥0，且x-2≠0，

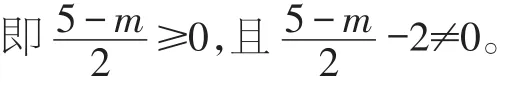
解得m的取值范围是m≤5且m≠1。

【点评】解决此题的关键是熟练掌握解分式方程的一般步骤，以及对分式方程解的意义的理解。

例3（2017·江苏兴化）已知关于x、y的方程组给出下列说法：

①当a=1时，方程组的解也是方程x+y=2的一个解。

③无论a取什么数，2x+y的值始终不变。

④若y=x2+5，则a=-4。

其中正确的是（ ）。

A.②③④ B.①②④

C.③④ D.②③

【分析】本题主要考查二元一次方程的解法，而解法的核心是消元，要会用含a的代数式分别表示x和y。

解：把a=1带入x+y=1-a，得x+y=0，故①是错误的；将x+y=1-a与x-y=3a+5相加，得：2x=2a+6，x=a+3，将x+y=1-a与x-y=3a+5相减，得：2y=-4a-4，y=-2a-2，x-2y≥8就转化为（a+3）-（-4a-4）≥8，解得：a≥，故②是正确的。

把2x+y转化为（2a+6）+（-2a-2），合并同类项，得2x+y=4，故③是正确的。

把方程y=x2+5转化为-2a-2=（a+3）2+5，即-2a-2=a2+6a+9+5，a2+8a+16=0，解得：a=-4，故④是正确的。

所以正确答案是A。

【点评】解决此题的关键是用含a的代数式分别表示x和y，并将题目中所涉及的不等式和方程转化为关于a的一元一次不等式和一元二次方程。

考点二：方程和不等式（组）的实际运用

例4（2016·山东济宁）某地2014年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规定投入资金逐年增加，2016年在2014年的基础上增加投入资金1600万元。

（1）从2014年到2016年，该地投入异地安置资金的平均增长率为多少？

（2）在2016年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天奖励8元，1000户以后每户每天补助5元，按租房400天计算，试求今年该地至少有多少户享受到优先搬迁租房奖励。

【分析】对第一问，设从2014年到2016年，该地投入异地安置资金的平均增长率为x。要注意2016年的投入资金是1280+1600=2880（万元），从而可列方程求解；第二问注意找到题目中数量之间的不等关系，即每户每天奖励8元的搬迁户的租房奖励总额+每户每天奖励5元的搬迁户的租房奖励总额≥500万。注意每户每天奖励8元的搬迁户有1000户，设每户每天奖励5元的搬迁户有y户，即可列出不等式求解，进而得到题目的答案。

解：（1）设从2014年到2016年，该地投入异地安置资金的平均增长率为x。

根据题意，得1280（1+x）2=1280+1600，

解这个方程，得x1=0.5，x2=-2.5（不合题意，舍去）。

答：从2014年到2016年，该地投入异地安置资金的平均增长率是50%。

（2）设今年该地有y户享受到优先搬迁租房奖励。

根据题意，得0.0008×1000×400+0.0005×400（y-1000）≥500，

解这个不等式，得y≥1900，

y≥1900的最小值是1900。

答：今年该地至少有1900户享受到优先搬迁租房奖励。

【点评】本题主要考查了一元二次方程及一元一次不等式的应用。我们要找出题目中能够反应数量关系的语句，并能正确列出方程和不等式。

考点三：方程、不等式（组）和函数知识的应用

例5（2013·江苏宿迁）在平面直角坐标系xOy中，一次函数y=x+2与反比例函数y=（x＞0）的图像交点的横坐标为x0。若k＜x0＜k+1，则整数k的值是_______。

【分析】先求反比例函数与一次函数的交点，联立两函数解析式，求出交点横坐标x0，将x0代入k＜x0＜k+1中，估算即可确定出k的值。

解：联立两函数解析式得：

配方得：x2+6x+9=24，即（x+3）2=24，

解得：x1=2-3或x2=-2-3（舍去），

∴一次函数与反比例函数交点的横坐标为x0=2-3，

∴整数k的值是1。

【点评】此题考查了一次函数与反比例函数的交点问题。确定两函数交点的横坐标是解本题的关键。对用消元法解方程组的核心知识的理解及寻求不等式的整数解也是解决此题的关键要素。

例6（2018·江苏南京）已知二次函数y=2（x-1）（x-m-3）（m 为常数）。

（1）求证：不论m为何值，该函数的图像与x轴总有公共点。

（2）当m取什么值时，该函数的图像与y轴的交点在x轴的上方？

【分析】本题是二次函数与一元二次方程、一元一次不等式的结合，二次函数的图像与x轴的交点个数是由相应的一元二次方程解的个数确定的。二次函数图像与y轴的交点的横坐标为0，此时对应的纵坐标大于0，即为问题要求的答案。

（1）证明：当y=0时，2（x-1）（x-m-3）=0。

解得x1=1，x2=m+3。

当m+3=1，即m=-2时，方程有两个相等的实数根；当m+3≠1，即m≠-2时，方程有两个不相等的实数根。

所以不论m为何值，该函数的图像与x轴总有公共点。

（2）解：当x=0时，y=2m+6，即该函数的图像与y轴交点的纵坐标是2m+6。

当2m+6＞0，即m＞-3时，该函数的图像与y轴的交点在x轴的上方。

【点评】正确解答此题的关键是明确函数图像与坐标轴交点的意义，进而将函数问题转化为方程和不等式问题。