踩点到位 分数到手

康 敏

“方程与不等式（组）”是初中数学最重要的基础知识之一，是数学中考的重点内容和必考内容之一。这类问题都是按照先学习定义，再学习解法，最后解决实际应用问题的顺序研究的。做这类题目，若抓住问题的本质，踩点解答，则可分数到手。

踩点就是踩对考试中某一些得分的点，也可以说答到点子上；踩点得分,其实就是分段得分。中考的阅卷评分办法是踩对了多少知识点就给多少分。踩点得分的基本思想是：学会“肢解”题目，多去争取踩分点，会做的题目力求不失分，部分理解的题目力争多得分，要有每分必争的信念。我们一起看下面的例题。

例1求不等式组的正整数解。

【解析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大取中间、大大小小无解，确定不等式组的解集，在这个解集的范围内找正整数解。

解：

解不等式①，得：x＞-2，（解一元一次不等式）

∴不等式组的正整数解是1，2，3，4。（写出整数解）

例2已知关于x的一元二次方程mx2+5x+m2-2m=0有一个根为0，则m=______。

【解析】根据一元二次方程的解的定义，由根为0，把m=0代入原方程，列出关于m的方程。通过因式分解法解关于m的一元二次方程，求得m的值。特别考虑一元二次方程的定义，二次项系数不为0，最终确定m的值即可。

解：∵关于x的一元二次方程mx2+5x+m2-2m=0有一个根为0，

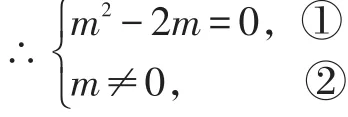
解①得m=0或m=2，（解一元二次方程）

综上得：m=2。（综合求出最终结果）

例3求证：不论m取何值，关于x的方程（x-1）（x-2）=m2总有两个不相等的实数根。

【解析】要判断一元二次方程的根的情况，就要想到一元二次方程的根的判别式，而求根的判别式的前提是一元二次方程是一般形式。计算出根的判别式的值为1+4m2，利用平方的非负性、不等式的性质判断出判别式的符号。

解：化简，得：

x2-3x+2-m2=0，（化一元二次方程一般形式）

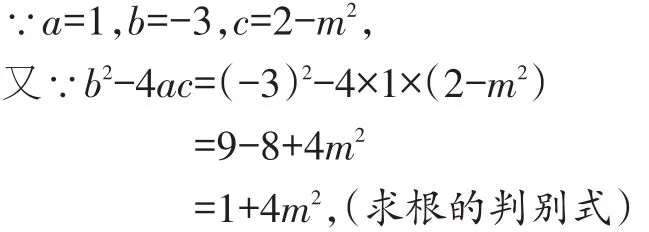
∵m2≥0，

∴4m2≥0，

∴1+4m2＞0，（判断根的判别式与0的大小关系）

∴b2-4ac＞0，

∴不论m取何值，关于x的方程（x-1）（x-2）=m2总有两个不相等的实数根。

例4已知a、b、c均为实数，且|b+1 |＋（c+3）2=0，求方程ax2+bx+c=0的根。

【解析】由二次根式非负性、绝对值的非负性、平方的非负性，可以得出3个分别关于a、b、c的一元一次方程，解一元一次方程，求出a、b、c的值，再把它们代入所求方程，最后用公式法或配方法求出一元二次方程的解。

解：∵≥0，| b +1 |≥0，（c+3）2≥0，且＋ |b +1 |＋（c+3）2=0，

∴a-1=0，b+1=0，c+3=0，（由具有非负性的3个整体之和为0得出方程）

∴a=1，b=-1，c=-3，（解一元一次方程）

把a=1，b=-1，c=-3代入ax2+bx+c=0得：

x2-x-3=0，（代入得方程）

即x1=。（解一元二次方程）

例5已知关于x的一元二次方程（x-3）（x-2）=p（p+1）。

（1）试证明：无论p取何值，此方程总有两个实数根。

（2）若原方程的两根 x1、x2满足 x12+x22-x1x2=3p2+1，求p的值。

【解析】（1）将原方程变形为一元二次方程的一般式，根据方程中各项的系数，计算出根的判别式b2-4ac的值，正好符合完全平方公式的特征，把它写为平方形式，即可证出：无论p取何值，此方程总有两个实数根；（2）由完全平方公式的变形，把x12+x22-x1x2=3p2+1转化为两根之和与两根之积的整体形式，这样就需要利用一元二次方程根与系数的关系，代入后化为关于p的方程，解出即可。同学们即使不会做第一问，也可以直接做第二问，得第二问的分数。

（1）证明：原方程可变形为x2-5x+6-p2-p=0，（化一般形式）

∵a=1，b=-5，c=6-p2-p，（求出根的判别式）

∴b2-4ac=（-5）2-4×1×（6-p2-p）=25-24+4p2+4p=4p2+4p+1=（2p+1）2≥0，

∴无论p取何值，此方程总有两个实数根。（配方后再判断）

（2）解：∵原方程的两根为x1，x2，且a=1，b=-5，c=6-p2-p，

∴x1+x2=-=6-p2-p，（计算根与系数关系）

又∵x12+x22-x1x2=3p2+1，

∴（x1+x2）2-3x1x2=3p2+1，（完全平方公式的变形）

∴52-3（6-p2-p）=3p2+1，（代入变为方程）

∴25-18+3p2+3p=3p2+1，

∴3p=-6，

∴p=-2。（解方程，求出p的值）

例6“绿水青山就是金山银山”。为保护生态环境，A、B两村准备各自清理所属区域养鱼网箱和捕鱼网箱，每村参加清理人数及总开支如下表：

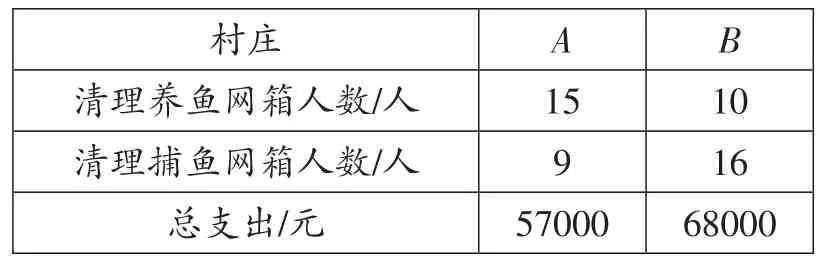
10 16 68000村庄清理养鱼网箱人数/人清理捕鱼网箱人数/人总支出/元A B 15 9 57000

（1）若两村清理同类渔具的人均支出费用一样，求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元。

（2）在人均支出费用不变的情况下，为节约开支，两村准备抽调40人共同清理养鱼网箱和捕鱼网箱，要使总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数，则有哪几种分配清理人员方案？

【解析】本题主要是二元一次方程组与一元一次不等式组的实际应用问题。（1）学会审题，找出已知量、未知量，设清理养鱼网箱的人均费用为x元，清理捕鱼网箱的人均费用为y元，根据A、B两村庄总支出的数量关系列出关于x、y的方程组，解之可得；（2）设m人清理养鱼网箱，则（40-m）人清理捕鱼网箱，根据“总支出不超过102000元，且清理养鱼网箱人数小于清理捕鱼网箱人数”列不等式组求解即可，特别注意最后的解要符合实际情况。

解：（1）设清理养鱼网箱的人均费用为x元，清理捕鱼网箱的人均费用为y元，

解这个方程组，得：x=2000，y=3000，（求出方程组的解）

答：清理养鱼网箱的人均费用为2000元，清理捕鱼网箱的人均费用为3000元。（写出答案得分）

（2）设m人清理养鱼网箱，则（40-m）人清理捕鱼网箱，根据题意，得：（列不等式组）

解这个不等式组得：18≤m＜20，（解不等式组）

∵m为整数，

∴m=18或m=19，（取整数值）

则分配清理人员方案有两种：

方案一：18人清理养鱼网箱，22人清理捕鱼网箱；方案二：19人清理养鱼网箱，21人清理捕鱼网箱。（分情况讨论并写出答案）

综上，我们看到，对于方程与不等式类题目，要仔细找准题目中的已知、未知量以及与之相关的数学知识，学会分析。我们要下功夫去研究其命题特点、解题切入点与解题模型，注重知识间的联系，万变不离其宗，学会找准知识点，能拿的分数一定要拿到。