强化理解，突破思维障碍

○申武广

积的变化规律是人教版小学数学四年级上册第四单元《三位数乘两位数》例题4的教学内容，在本课的教学过程中，多数学生能够在老师的引导下很快得出变化规律，但在解决“做一做”的第二题（如下图）时却出现了意想不到的困难。

有的学生不理解题意，有的学生不知从何处下手，有的把算式列错，还有的用以前的方法列出了算式。为了让学生真正掌握好这道题，我在教学中进行了如下尝试，效果较好。

师：同学们，要解决一道题，首先要干什么？

生：理解题意。

师：说得对！通过认真读题，你觉得哪儿是需要大家注意的？

生：增加到

生：扩大后

师：什么是“增加到”？

生：“增加到”就是增加之后的长度。

生：也就是说原来8米，后来成了24米，就是增加后的结果。

师：那么它跟“增加”有什么区别呢？

生：“增加”就是多出来的部分，而“增加到”是变化之后的总数。

生：我们这里的宽是8米，增加到24米，那么增加的是16米。

师：两位同学说得好！看来，“增加”和“增加到”确实不一样，“扩大后”的意思相信同学们也明白了。那么，从8米到24米，你看出了什么变化吗？

生：宽扩大了3倍。

师：你能运用今天所学知识解决问题非常棒！为了让大家看得更清楚，我们来看大屏幕（出示PPT）

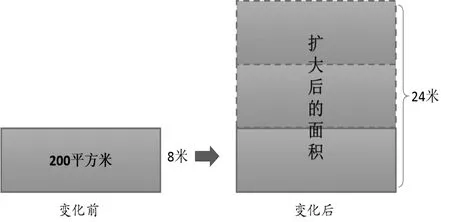
教师通过展示课件介绍草坪面积变化过程，再次通过直观强化理解“增加到”和“扩大后”的含义。

师：刚才我发现部分同学运用了以前学过的方法，谁来介绍一下？

生：我是这样做的，已知草坪的面积和宽，可以求出草坪的长，200÷8=25米，因为长是不变的，现在的宽是24米，那么面积就用长乘宽，25×24=600平方米。

师：大家听懂了吗？根据我们学过的长方形面积计算方法可以求出本道题。现在我们是四年级了，换一个思考角度，你能运用今天所学的积的变化规律来解决这道题吗？请大家再想一想。

（学生独立思考，然后小组交流讨论。）

生：我们小组认为，根据宽由8米增加到24米，可知宽扩大了3倍，因为长不变，所以面积也会扩大3倍，直接用200×3=600平方米。

师：老师还有个地方不很明白，为什么在长不变的情况下，宽扩大3倍，面积就扩大了3倍呢？

生：因为“长×宽=长方形的面积”，长和宽分别是因数，面积是两个因数的积。我们刚学习了“一个因数不变，另一个因数扩大（或缩小）若干倍，积也扩大（或缩小）相同的倍数”，所以当长不变的情况下，宽扩大3倍，面积就扩大了3倍。

（师生为这位学生的发言鼓掌。）

师：同学们，老师对刚才的题进行了稍微的改编，你能做对吗？

教师出示下面三道练习题：

1.游乐场准备扩建一块长方形草坪，这块草坪原来的面积是540平方米，宽是9米。如果长不变，宽增加27米，草坪增加的面积是多少平方米？

2.游乐场准备扩建一块长方形草坪，这块草坪原来的面积是540平方米，宽是9米。如果长不变，宽增加27米，草坪增加后的面积是多少平方米？

3.游乐场准备扩建一块长方形草坪，这块草坪原来的面积是540平方米，宽是9米。如果长不变，宽增加到27米，草坪增加后的面积是多少平方米？

对于四年级学生来说，初次接触这样的问题情境，或多或少会遇到一定的困难。因为在学习这部分内容之前学生接触更多的是“扩大多少倍或缩小多少倍”的说法，“增加到”往往理解成“增加了”，并且在涉及到“倍”的变化时，也会把“增加多少倍”和“扩大多少倍”混淆。为了突破难点，教师首先引导学生从文本阅读开始，找出较难理解的词语进行比较，辨析概念的确切含义，这样学生对“增加到”“扩大后”等词语才会有深入的认识；同时，借助图示帮助学生理解，从变化前到变化后，原来的部分与变化的部分，学生从图中看得一清二楚，头脑中留下了清晰的印象，收到了很好的教学效果。

不仅如此，老师没有硬性要求学生运用积的变化规律来解本题，而是尊重学生的认知现实，利用面积计算公式来求本题，然后在此基础上，进一步引导学生从积的变化角度来审视，并且追问：为什么宽扩大3倍，面积也扩大3倍呢？从而有效凸显了今天所学的积的变化规律，使得学生对规律的认识愈加深刻明晰。同时，为了进一步巩固学生的理解，老师为学生提供了三道练习题，数据和条件看似相同，却有区别：一个是宽的变化，一个是面积的变化。学生在这样的变式练习中，思维会更加灵活，分析问题的能力也会增强，为以后相关内容的学习奠定坚实的基础。