《怎样围面积最大》教学

黄 建

【教学内容】

人教版六年级拓展课。

【教学目标】

1.根据周长相等的条件，100%的学生能够围出不同的图形并计算面积，90%的学生进一步明确周长相等的情况下，圆的面积最大。

2.60%的学生能够用数学语言完整地表达推理过程，能总结概括出研究报告的要素，并通过多样化的表达形成研究报告。

【课前思考】

什么是数学学科的表达能力？我们该如何培养？数学表达能力是指运用语言文字阐明自己的数学观点、意见或抒发思想、感情的能力。它包括口头表达能力、文字表达能力、数字表达能力、图示表达能力等几种形式。同时数学语言的表达也是学生对知识的掌握程度的一种反映。

数学交流表达的几个表现层次：1.（语句）完整；2.（逻辑）严密；3.（用词）准确；4.（语言）简洁；5.（方式）多样。

于是，在学生经历了长方形（正方形）、平行四边形、三角形、梯形、圆的面积公式推导、掌握这些平面图形的面积公式，明确一些图形之间的面积关系——当周长相等的情况下，正方形的面积大于等于长方形的面积等之后。我们设计了这样一个小课题研究，而小课题研究的本质上是这样一个数学问题：当周长相等的情况下，围成什么图形的面积最大？基于这样一个数学问题，我们是怎么样培养学生的达能力呢？在这一节课中，我们引导学生通过猜测、验证等过程培养学生数学表达能力这一关键能力。在第一环节中，学生通过表达明确小课题研究的主题、研究内容；在第二环节中，学生通过计算、推理等过程进行验证，与此同时，尤其关注学生数学表达的完整性、逻辑的严密性、用词的准确性与语言的简洁性。当然，这些都是教师评价学生语言的重要标准。在第三环节中，鼓励学生用多样化的方式进行表达。

【教学过程】

一、确定研究主题（预：5 分钟）

1.出示情境。

师：今天，我们要解决这样一个问题。你会围成什么图形？

生：三角形、长方形、正方形、梯形、圆等。四边形、五边形、六边形等。

小结：但是不管怎么围什么是不变的，什么变化？

2.数学思考。

师：我们要解决这个问题，就是在研究一个什么数学问题？

出示课题：周长相等的情况下，什么图形的面积最大？这就是我们今天研究的主题。

3.交流讨论。

师：说到面积，这么多的图形，哪些图形的面积现在是能够确定的？我们来算一算。（按π=3 计算）

生：正方形边长24÷4=6（米），S正=6×6=36（平方米）；圆形半径r=24÷3÷2=4（米），S圆=3×4×4=48（平方米）。

师：哪些图形现在是能比出大小的？

生：长方形＜正方形，这是我们已经学过的知识。

师：这么多图形，我们能不能分分类？

分类：三边形、四边形、圆。

4.猜测。

师：现在，你能不能大胆猜测一下，哪个图形的面积最大？

生：我觉得圆的面积最大，正方形的面积第二大。

二、讨论研究方案

1.确定研究方案。（预：2 分钟）

师：这只是我们的猜测，你打算怎么来验证？

生：我觉得围成各种各样的封闭图形，然后计算这个封闭图形的面积，最后比较它们的面积，得出结论，看看是哪个图形的面积最大。

（小组讨论，确定研究方案）

师：他想到了操作（板书），那我们不可能真的用一根24 米长的绳子怎么办？

生：那很简单，用24 厘米的绳子代替24 米的绳子。

师：如果每个图形都去研究时间肯定不够，你有什么好方法？

生：我觉得可以这样，我们小组内每人选择一种图形来围。这样能节省时间，而且也可以看看其他组和你围的图形一样的同学。这样就可以看到很多图形了，并且节省时间。

2.合作研究。（预：8 分钟）

师：就按照同学们说的做。

3.全班交流。（预：6 分钟）

师：你们是怎么来就研究的，研究结论是什么？

（1）平行四边形的面积。

生：我们是四人小组合作，我们分别研究了平行四边形、三角形、梯形这三类图形。我研究的是平行四边形，你们看我围出的这个平行四边形，通过计算我发现这个平行四边形的面积是24 平方厘米。所以我发现圆的面积最大。（黑板上记录）

师：同样是研究平行四边形，有没有比这个图形面积更大的图形？你围的图形的面积是多少？

生：我围得的也是平行四边形，它的面积是58.5平方厘米。

生：我觉得根本不可能，你看看我们知道周长是24 厘米。底是6.5 厘米，斜边最多5.5 厘米。这一条高是9 厘米，高一定比斜边短，9＞5.5。根本不可能。

师：能听懂吗？是的！底边是5.5 厘米，则这一条也是5.5 厘米，那么周长是24 厘米，24-5.5×2=13（厘米），斜边就是13÷2=5.5（厘米）。而斜边要大于等于直角边，9＞5.5，不可能。

小结：周长相等的情况下，平行四边形的面积小于圆的面积。

（2）三角形的面积。

生：我研究的是三角形，你们看我围出的这个三角形，通过计算我发现这个三角形的面积是28.9 平方厘米。所以我发现圆的面积最大。（黑板上记录）

师：同样是研究三角形，有没有比这个图形面积更大的图形？你围的图形的面积是多少？对于三角形，还有没补充的？

小结：周长相等的情况下，圆的面积最大。

（3）梯形的面积。

生：我研究的是梯形，你们看我围出的这个梯形，通过计算我发现这个梯形的面积是35 平方厘米。但是它的面积要比圆小。所以我发现圆的面积最大。（黑板上记录）

师：同样是研究梯形，有没有比这个图形面积更大的图形？面积是多少？对于梯形，还有没有补充的？

小结：周长相等的情况下，圆的面积最大。

（4）小结提升。

生：综上所述，我们发现，当周长相等的情况下，圆的面积最大。

师：到目前为止，我们通过操作总结得出这样一个结论。但我们是不是就能说，这个结论一定是正确的呢？

生：我觉得是正确的！

生：我觉得是更有信心了！但是我还是不怎么确定，你看！我们只是研究了三边形、四边形、圆，那还有五边形、六边形等我们都没有研究过呢！

生：我也觉得，那不一定，哪怕是三角形、梯形、平行四边形还有很多种，我们只是举了其中几个例子，我们觉得还不是特别有说服力。

4.推理论证（控制高不变）。（预：8 分钟）

师：怎么样变得更有说服力呢？既然我们已经知道了S正＜S圆，现在，我们把这四个周长相等的图形放在一组平行线之间，你知道了什么？

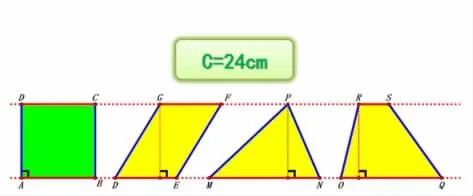
生：我知道了这几个图形的周长是相等的！

生：两条平行线之间距离处处相等，所以高也相等，都是6。

师：周长相等、高相等，它们的面积和正方形的面积有什么关系呢？小组里互相交流一下。

生：周长相等，当高相等时，因为平行四边形的斜边比正方形的边长长，所以平行四边形的底比正方形的底短；又因为高相等，所以平行四边形面积小于正方形的面积。

师：说得很完整、也很有逻辑性，但是不够简洁，谁愿意上来指着这个图形再来说说看？

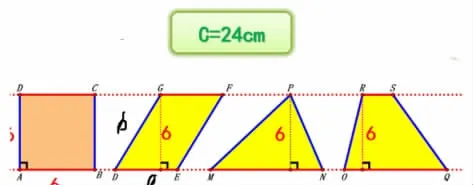
生：b 大于6，所以a 小于6。高相等，所以S平小于S正。

生：其实可以这样理解，b 一定是大于6 厘米的，所以它的对边也大于6 厘米，而又因为周长是24 厘米，所以2a 一定小于12，a 小于6。S平=a×6，S正=6×6，a 小于6，所以S平小于S正。

师：在表述过程中，借助字母可以让我们说得更简洁、更清楚。那梯形和三角形呢？为了便于你们交流，我们也标上字母任选一个，和你的同桌说一说。

生：c+d 大于12，所以a 小于12。高相等都是6，S△=a×6÷2，S正=6×6，a÷2 小于6，所以S△小于S正。（教师板书）

生：c+d 大于12，所以a+b 小于12。高相等都是6，S梯=（a+b）×6÷2，S正=6×6，（a+b）÷2 小于6，所以S梯小于S正。

师：你们觉得他们说得怎么样？

师：你看，我们又作了这样的推理，当周长、高相等的情况下，它们的面积永远小于正方形的面积，又因为正方形的面积小于圆的面积。所以，圆的面积最大。现在，是不是更有信心了？

5.进一步推理论证（底、高都变化）。（预：6 分钟）

师：刚才我们发现，四边形中哪个图形的面积最大？（出示正四边形）那三边形呢？

生：我觉得是正三角形面积最大。

生：我觉得是等腰直角三角形面积最大。

（1）底不变，从一般三角形→等腰三角形。

师：任意一个三角形，如果它的底不变，另一个顶点可以移动，什么时候面积最大？（操作）为什么？

生：底相等，高最大的时候，面积最大。生：所以周长相等时等腰三角形面积最大。

（2）等腰三角形→等边三角形。

①想象：继续想，同样是等腰三角形，什么时候面积最大。

②操作：请你选择一个三角形，找一找面积最大的等腰三角形。

生：我觉得是等边三角形面积最大。

③验证：我们来看一下对不对！（几何画板操作）

生：我们猜对了，当它是正三角形的时候，面积最大是27.8 厘米。

（3）回顾。

师：刚才，我们是怎么找到三边形中面积最大的图形？

生：当底相等的情况下，等腰三角形的面积最大，同样是等腰三角形时等边三角形的面积最大。

师：而正三角形的面积比正四边形的面积小，比圆的面积小，所以还是成立的。

6.总结回顾。

师：同学们！刚才我们通过这样的研究得出什么结论？是用什么方法研究的？

生：计算、推理（和正方形比较，找到周长相等、同一类中面积最大的图形）。

师：我们不仅得出了这样的结论，还发现三边形时，什么图形的面积最大？四边形时？那如果是五边形、六边形？几边形呢？有兴趣的同学可以自己去研究。但是到目前为止，我们发现，周长相等的情况下，圆的面积最大。

三、形成研究报告

师：今天，我们研究了一个非常了不起的小课题。需要把整个研究过程记录下来，如果让我们写一份研究报告，你打算从哪些方面撰写？

生：我们觉得研究报告，首先要有标题；有了标题之后，得有研究主题，就是研究的是什么；而且还要写研究的方案，我们是打算怎么来研究的；接着在研究过程中，我们是分成哪几类情况进行研究，对于同一类，我们又用了哪些方法；最后，我们的研究成果是什么。

师：刚才他说到了几个关键词，研究主题、研究方法、研究过程和研究结论。请你从这几个方面把刚才的研究过程进行整理。

四、多样化表达

（学生作品略）