笔算除法为什么不从个位算起———《笔算除法》起始课教学的实践与思考

林 霞 陈珍珍

《笔算除法》是小学计算教学中特别重要的知识，也是一个老大难的问题。以前，老师们都把笔算当作计算的一项技能来训练，认为笔算没有思维含量。近几年，随着“算理比算法更重要”理念的不断深入，我们开始追究“规定性知识”背后的原因。在新理念影响下，我们进行了一次笔算除法教学的大胆尝试。

人教版三年级下册开始系统学习除数是一位数的笔算除法，教材在二年级下册已经安排过表内除法竖式的学习，但差不多隔了一个学年，相信学生已经把除法竖式忘得差不多了。为此，教材也在教学本内容之前安排了一道笔算复习题（如图1）。

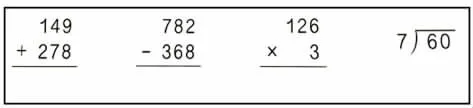
图1

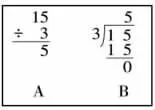
图2

看着长相和其他竖式如此不同的除法竖式，不禁想起了俞正强老师教学表内除法竖式的起始课，俞老师把“为什么除法竖式是这样（图2 的B），而不是这样（图2 的A）”作为笔算教学的突破口，让学生感受“数学规定是讲道理的”。那么，今天这节课又有什么地方可以突破，有什么道理可讲呢？本文试着运用蔡金法教授团队的分析框架，运用数学分析、认知分析和教学分析三个方面分析笔算除法起始课的教学。

一、数学分析

笔算除法教学主要分为三个阶段：一是“表内除法竖式”，首次接触除法竖式；二是“除数是一位数除法”，真正进入除法竖式理解性学习阶段；三是“除数是两位数的除法”，属于除法竖式的完善阶段。现行人教版教材分别安排在二下、三下和四上来学习。分析教材我们发现，二下首次安排笔算除法，主要是认识除法竖式的书写格式以及每一部分的名称，运用“表内除法”的口算能力直接试商，商是一位数，除法竖式也只有一层。三下的笔算除法是安排在“除数是一位数除法”这一单元，起始课教学的两个例题商均为两位数，竖式要写成两层。例1 教学“首位能整除”的42÷2，例2 教学“首位不能整除”的52÷2。教材借助直观操作帮助学生理解除法竖式每个步骤的意义和作用，进而领悟到除法竖式的计算方法。

除法竖式与加、减、乘三种竖式不仅在书写形式上差别较大，在计算顺序上更是完全相反。教学加、减、乘竖式时，一直强调要从个位算起比较方便，而在除法竖式计算时，却强调从高位算起比较方便，这一任务需要在三下教学“笔算除法”起始课中解决。对于例1“首位能整除”的42÷2 来说，从十位算起和从个位算起在简便程度上看是没有区别的，只有到例2“首位不能整除”的52÷2，从十位算起要比从个位算起更加简便。

二、认知分析

对于两位数除以一位数的笔算除法，三下学生的思维是怎么样的呢？我们想到了通过“前测、访谈”加以了解。为了扫除障碍，引发学生用竖式解决问题，在前测中安排了“表内除法除式”的复习，帮助学生回忆除法除式的书写格式、各个部分的名称和每一个数表示的意义。

前测在非正式上课的班级（48 人）进行，呈现“把52 个羽毛球平均分给两个班”的情境，让学生写出计算的思考过程，要求尽可能用多种方法解决。

学生的原有认知是怎么样的呢？分析测试结果发现，采用画图法的有18 人，占测试总人数的37.5%；用列横式分步口算法的有35 人，约占72.9%；用文字表达分法的4 人，约占8.3%；选用竖式计算的学生只有7 人，约占14.6%；仅有2 人用标准竖式正确表达。从擦拭痕迹来看，部分学生尝试过竖式计算，但没有成功。

在分步口算法的35 个学生中，我们又进行了统计，发现把52 分成50 和2 是学生最直接的方法，仅有2 人是把52 分成40 和12 来计算的。这和以往做加、减、乘法时把两位数看成整十数和一位数来计算是一致的。继续分析学生的口算方法，可以明显地看出，学生的计算顺序也是不同的，有先算个位的2÷2=1，也有先算50÷2 的，先算个位的比例更高一些。我们发现，在学生认知中，先算个位和先算十位都能解决问题，不存在大的差异。

从以上认知分析得知，学生对于笔算除法的顺序的理解是一道“坎”，如何能在起始课教学中帮助学生顺利跨过这道坎，享受一次讲道理的数学课堂呢？

三、教学分析

通过数学和认知两方面的分析，我们大胆地进行了以“笔算除法为什么不从个位算起”这一问题展开的教学实践，让教材中安排的两个例题承载不同的教学目标。

1.记录分物，理解两层竖式的必要性和含义。

从前测中，我们了解到学生对除法竖式的认知停留在“表内除法”一层竖式阶段，如何使学生产生从一层竖式到两层竖式的需求，我们进行了记录分物的活动。

教师出示42 根（4 捆2 根）小棒，要求学生平均分成2 份，让学生口述分法。为了先感受高位算起的竖式，这个环节有两种预设：一是第一位学生就是先分整捆的，直接开始记录，记录完成后再问学生有没有不同分法；二是如果第一位学生是先分散根的，等他说完分法后紧接着问其他学生有没有不同分法，等两种分法都表达完后，教师提议先记录第二位同学的分法。操作步骤如下：

（1）尝试记录分小棒过程。

教师分小棒，学生用竖式记录42÷2（从高位开始）。

首先，教师把4 捆小棒平均分成2 份，边分边说：先把4 捆小棒平均分成2 份，每份2 捆，4 捆小棒刚好分完。

接着，教师把2 根小棒平均分成2 份，边分边说：再把2 根小棒平均分成2 份，每份1 根，2 根小棒刚好分完。

（2）反馈交流。

先由学生说说自己记录下来的竖式所表达的含义。接着教师抛出问题：上面两个竖式，哪一个竖式更能体现出刚才分小棒的过程呢？学生表达自己的想法。

有学生表示两层的竖式更好，因为刚才老师是分两次分小棒的，写成两层更清楚。

（3）再次记录42÷2（从个位开始）。

这个步骤与前面相似，要求学生再次记录分小棒的过程，不同的是这次是先分散根的小棒。教师为了了解更多的学生是如何记录的，请了一位学生上展台分小棒。

学生分2 根，每份1 根，教师配合学生分的过程说：先分散的2 根，每份1 根，正好分完。

学生再分4 捆，每份2 捆，教师配合学生分的过程说：再分整的4 捆，每份2 捆，正好分完。

（4）再次反馈。

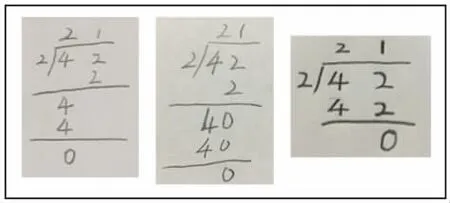
教师引导比较这三个竖式，学生认为前面两个竖式都写成两层，差不多。第三个竖式又把两个步骤并在一起了。小棒分法变了，竖式还是和刚才一样，这样的竖式看不出是先分整捆还是先分散根的。

（5）得出结论。

教师把分小棒的过程分两次呈现，每一次的记录与表内除法竖式是相通的，学生记录起来比较顺利。这样既分散了记录竖式的难点，又帮助学生感受写成两层的必要性，也为后面记录52÷2 做好了准备。

2.运用记录方法，经历并感受不同顺序的竖式。

在上面的步骤中，学生通过竖式记录了两种不同的分法，熟悉了两层竖式记录两次分小棒的操作方法。在这一环节中，希望学生经历“十位不能整除”时两种不同分法的记录，感受到个位算起所带来的麻烦，从而明白笔算除法不能从个位算起的道理。

（1）学生操作（52÷2）。

教师给每位学生准备了52 根小棒，要求学生平均分成2 份。学生操作，教师巡视，寻找两种不同分法的学生上台展示。

（2）反馈分法。

生1：我是先分整捆的，5 捆小棒平均分成2 份，每份2 捆还多出1 捆，把这1 捆和散的2 根合起来是12 根，再平均分成2 份，每份6 根，这样每份分到26 根。

生2：我是先分散根的，2 根小棒平均分成2 份，每份分到1 根，再分整捆，5 捆小棒平均分成2 份，每份2 捆还多出1 捆，最后把剩下的这1 捆拆开后再分，每份分到5 根。

（3）竖式记录（从高位开始）。

教师要求学生先回忆生1 的分法，然后按教师的分法用竖式记录。

教师边分边说：先分整捆，把5 捆小棒平均分成2 份，每份最多分到2 捆，分了4 捆，还剩下1 捆。

教师继续分小棒，边分边说：接着把剩下的1 捆和散的2 根合起来是12 根，12 根小棒，平均分成2份，每份6 根，分了12 根，小棒正好分完。开始记录！

（4）反馈辨析。

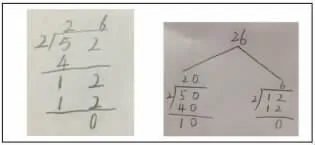
教师引导学生说说对上面两种竖式的看法。学生认为右边这个竖式有问题，50 除以2 余数10，余数是不能比除数大的，也有学生表示写成两个竖式麻烦，一致认同左边的竖式。

（5）再次记录（个位算起）。

学生叙述分法，教师根据学生的叙述分小棒。

生：生2 是先分散根的，把2 根小棒平均分成2份，每份分到1 根。

师：散的2 根分完了。开始记录！

生：接着分整捆的，5 捆小棒平均分成2 份，每份最多分到2 捆。

师：这样一共被分掉了4 捆，还剩下1 捆。开始记录！

生：还剩下1 捆，把这1 捆拆开就是10 根，10根小棒平均分成2 份，每份分到5 根。

师：剩下的1 捆小棒也被分完了。开始记录！

此时，部分学生表示出困难。教师让有困难的同学和同桌讨论讨论，看看同伴之间能不能解决。

（6）反馈比较。

不少学生没有完成记录，教师找到两张记录完整的作品，呈现给学生看，并要求学生观察比较，说说想法。

有学生表示看不懂，而记录的两个学生说：跟着老师分的节奏我只能这样记，要不然就没办法了；散的小棒分了还要再分，记录起来太麻烦了。

此时，有学生站起来说：如果从散根开始分，十位除以除数没有余数那还没事；如果十位除了以后还有余数，就要再分。以后数再大起来，真不知道该怎么办了。

四、课后思考

本节课在数学分析和学生认知分析的基础上，创造性地以“笔算除法为什么不从个位算起”这一大问题展开教学，学生的收获是非常大的。通过例1 首位能整除的42÷2 教学，使学生经历记录两种不同顺序的分小棒过程，感受两层竖式的必要性以及每一个步骤的含义，此时学生对运算顺序是没有认知冲突的，先算个位和先算十位都很顺，但在例2 首位不能整除的52÷2 的教学时，学生再次记录两种不同顺序的分小棒过程时，就对运算顺序产生了冲突。在亲身经历竖式的记录过程后，学生的感受特别深刻。畅谈学习收获时，课前认为笔算除法也和加、减、乘法一样从个位算起的学生，就说到自己明白了要从十位算起的原因；思维能力好的学生还联想到当数位更多时，麻烦也就更大；最让人欣喜的是，学生还能把两个例题结合起来总结，发现问题的本质：如果每一位都整除，两种顺序都是可以的，但如果前面有哪一位不能整除，从个位算起就会带来麻烦。

学生的精彩就是课堂的精彩，教师放慢脚步赢得学生的精彩，是教师最大的欣慰，也是我们一线教师研究课堂教学的动力。