一类含有时滞的分数阶Laplacian方程共振边值问题解的存在性

郑春华，马 睿

(陕西工业职业技术学院 基础部,陕西 咸阳 712000)

0 引言

虽然分数阶微积分的讨论始于微积分的发明人莱布尼兹，但由于它刚开始出现时缺乏实际应用背景，关于分数阶微积分的研究一直进展缓慢并且主要局限于理论上的讨论.近几十年来，分数阶微积分特别是分数阶微分方程在粘弹性力学、电分析化学、生物电传导等科学与工程中的应用越来越广泛，分数阶微分方程的研究受到科研人员和数学工作者的青睐[1-4].分数阶微分方程边值问题的研究作为微分方程边值问题研究中的一个新课题，由于其应用的广泛性，吸引了诸多科学研究人员和数学工作者的重视，已经出现了一些优秀的研究成果[5-9].

文献[5]以Krasnoselskii不动点定理和Leggett-Williams不动点定理为工具研究了问题

正解的存在性.

以文献[6]的工作为基础，文献[7]的作者利用Krasnoselskii不动点定理研究了相同边值条件的含参数边值问题

得到了其正解的存在性.

鉴于p-Laplace算子丰富的应用背景， Laplacian方程边值问题的研究一直都是微分方程研究的热点问题.经过广大科研人员的努力，含有p-Laplace算子分数阶微分方程边值问题的研究结果已经出现了一些结果.陈太勇先生利用重合度理论在共振条件下讨论了分数阶微分方程两点边值问题

解的存在性[10].

刘锡平先生利用压缩映射原理研究了分数阶微分方程两点非共振边值问题

解的存在性[11].

由于时滞微分方程在实际应用中的重要作用，关于它的研究已经取得了大量的成果，但对于含有时滞的分数阶微分方程边值问题的研究工作还不是很多[12-18].在以上研究工作的基础上，我们利用Mawhin连续性定理讨论了具有时滞的两点共振边值问题

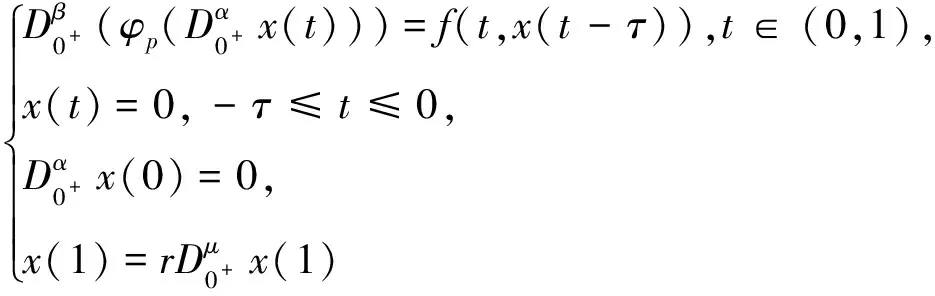
(1)

1 预备知识

定义1[3]设α>0，定义函数f(t)的α阶Riemann-Liouville型分数阶积分为

定义2[3]对于函数f(t)和α>0，定义f(t)的α阶Riemann-Liouville型分数阶导数为

其中n=[α]+1.

引理1[5]对于α>0，u∈C(0,1)∩L(0,1)，则分数阶微分方程

有唯一解u(t)=c1tα-1+c2tα-2+…+cntα-n，其中ci∈R(i=1,2…,n).

引理2[5]对于α>0，u∈C(0,1)∩L(0,1)，则存在ci∈R(i=1,2…,n)使得

引理3[2]当β≥0，α+β≥0，u∈L(0,1)时有

引理4[8]对于μ>0，N=[μ]+1，则

引理5[8]F⊂Cμ[0,1]为列紧集的充要条件是F一致有界且等度连续.

引理6[19]设X和Y为2个Banach空间，L:D(L)⊂X→Y为零指标的Fredholm算子，Ω⊂X是一个有界开集，N：Ω×[0,1]→Y且L-紧，如果下列条件满足

1)Lx≠λNx，∀(x,λ)∈[D(L)∩∂Ω]×(0,1)；

2)Nx∉lmL，∀x∈∂Ω∩KerL，

3) deg(JQN,Ω∩KerL,0)≠0，

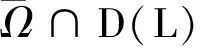
引理7边值问题(1)等价于下面的边值问题

(2)

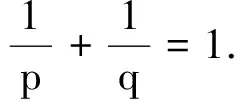
故x(t)必为边值问题(2)的解.

显然，问题(2)的解也为问题(1)的解.

令

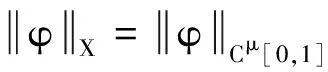
定义算子

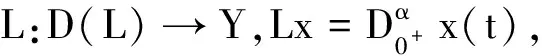
引理8对于算子L有

KerL={x|x∈X,x=ctα-1,t∈[0,1],c∈R}，

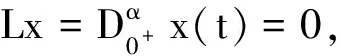
KerL={x|x∈X,x=ctα-1,t∈[0,1],c∈R}.

对

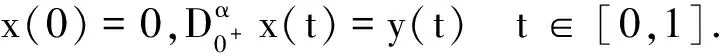
进而可得

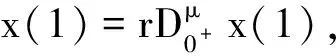
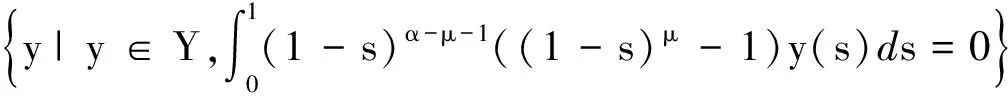
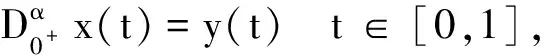
即

也即

.

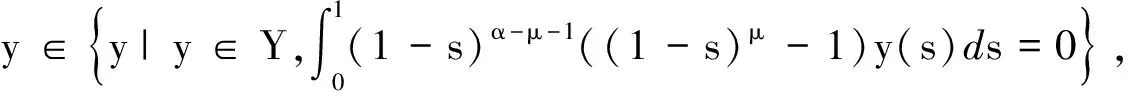
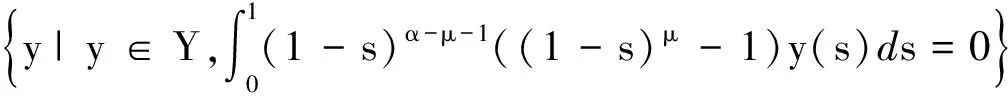
引理9L为零指标的Fredholm算子.

证明定义投影算子

易知KerQ=lmL，Y=lmL⊕lmQ.故L为零指标的Fredholm算子.

定义投影算子

容易验证lmP=KerL，X=KerL⊕KerP.

记LP=LD(L)∩KerP:D(L)∩KerP→lmL，则LP具有连续的逆算子LP-1且

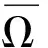
证明引例10的证明和参考文献[14]中引理9的证明完全类似，在此不再赘述.

2 主要结果及证明

定理1设连续函数m(t),n(t)和常数t0>0,r0>0满足下列条件：

A1) 对∀x,y∈R，t∈[0,1]有

|f(t,x)|≤m(t)+n(t)|x|,

A2)对∀x∈domL且|x(t)|>r0,t∈[t0,1]，有

A3)p>2或

则边值问题(1)至少有一个解.

证明考虑边值问题(2)对应的辅助问题

(3)

显然边值问题(3)等价于算子方程Lx=λNx.

下面估计边值问题(3)解的先验界.

令Ω1={x|x∈D(L)∩X,Lx=λNx,λ∈(0,1)}，对任意的x(t)∈Ω1，则有Lx=λNx，即λNx∈lmL=kerQ，进一步有QNx=0，即

也即

(4)

则由(4)式和条件A2)可找到t1∈[t0,1]满足|x(t1)|≤r0，再利用引理2和条件x(0)=0可得

故有

所以

从而可知

进一步可得

利用条件A1)可知

令Ω2={x|x∈KerL,Nx∈lmL}，则对任意的x(t)∈Ω2，有

其中c为常数.因为Nx∈lmL故QNx=0，从而可以得到

由条件A2)可知存在t2∈[t0,1]满足|ct2α-1|≤r0,进而可得

故有

显然，Ω2有界.

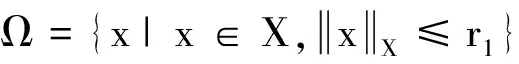
取同伦映射为H(x,λ)=λx+(1-λ)JQNx，显然有

H(x,λ)=λr2tα-1+(1-λ)QNxtα-1=(λr2+(1-λ)QNx)tα-1≠0，

因此，

deg(JQN,Ω∩KerL,0)=deg(H(x,0),Ω∩KerL,0)=deg(H(x,1),Ω∩KerL,0)≠0.