(1+1)维积分微分 Ito方程的精确行波解

宋佳谦,刘小华,郑任翔

(贵州民族大学 数据科学与信息工程学院,贵州 贵阳 550025)

非线性微分方程大多用来描述重要的非线性自然现象,随着非线性数学模型和方程的逐步建立和完善,许多求解非线性微分方程的经典求解方法也日益发展和建立起来,比如:Backlund变换法[1]、Hirota双线性法[2]、Darboux变换法[3]、Jacobi椭圆函数展开法[4]等,辅助方程法是一种常用于求解非线性微分方程精确解的方法,Ma等[5]利用辅助方程法考虑了Zakharrov-Kuznetsov方程的精确解.Liu等[6]用此方法得到了(2+1)维色散长波方程的精确行波解.

本文主要探讨(1+1)维积分微分Ito方程:

(1)

1 奇点分析和相图

在方程(1)中做变换u=vx,可将积分微分Ito方程(1)转换成如下的等价方程

vttx+vxxxxt+6vxxvxt+3vxvxxt+3vxxxvt=0,

(2)

对方程(2)进行行波变换,令v(x,t)=v(ξ),其中ξ=x-kt,k是波速,方程(2)可化为

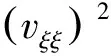
(3)

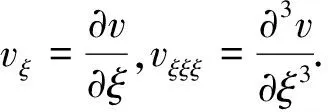
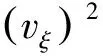
(4)

做变换w=vξ,方程(4)可化为如下等价的方程

3w2+wξξ-kw=0.

(5)

综上推导可知,方程(5)的解为w=vξ,而方程(1)的解为u=vξ,显然方程(1)的解与方程(5)的解具有相同形式.为此我们下面只须对方程(5)的有界行波解进行分析.

令wξ=xξ,w′ξ=yξ,则方程(5)等价于如下平面动力系统

(6)

易求得系统(6)具有首次积分为

(7)

为讨论方程(5)的有界行波解,下面对平面动力系统(6)进行有限远奇点分析.

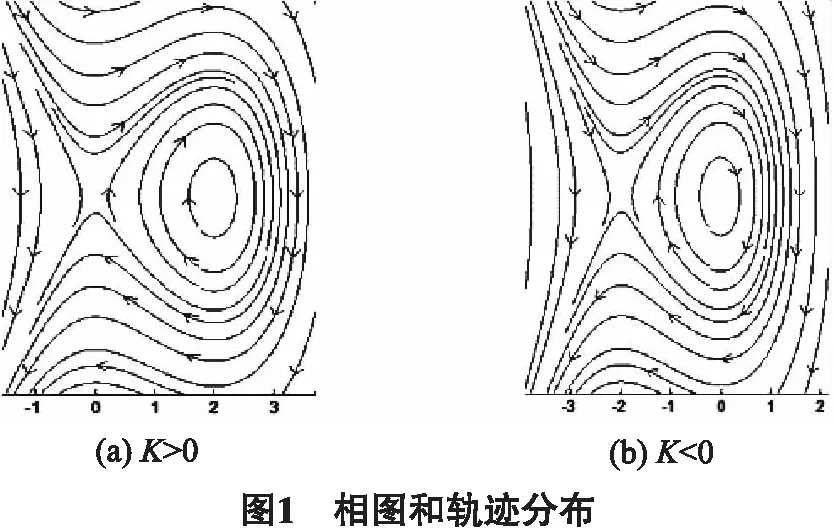
由图1(a)、(b)的相图和轨迹分布可知,系统(6)存在无数条闭轨,2条同宿轨,无数条有界轨.由于平面动力系统理论和方法系统(6)的同宿轨对应着方程(5)的钟状孤波解,闭轨对应着方程(5)周期解,有界轨对应着方程(5)的有界行波解.

综上分析可得,方程(5)的有界行波解如性质1所述.

性质1 1)当k>0时,方程(5)存在一个钟状孤波解u(ξ),u(ξ)→0,ξ→±∞ ,无数个周期解和无数个有界行波解.

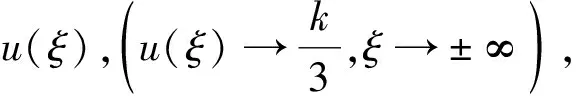
2 方程(1)的精确行波解

由上节的定性分析结论,本节将利用辅助方程法对方程(1)的精确行波解进行研究.首先给出辅助方程法的步骤.

2.1 辅助方程法

考虑如下的常微分方程为

Pwm,wm-1,…,w′,w=0.

(8)

步骤1 假设(8)有如下形式的解

(9)

其中ai(i=0,1,…,s)为待定系数,F(ξ)满足如下方程

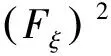
(10)

其中方程(10)的精确解见文献[11];

步骤2 由齐次平衡法确定方程(9)中的s,求出w(n),w(n-1),…w1,w,代入方程(8),得到一个关于a0,a1,…as的代数方程组;

步骤3 求解代数方程组,得到待定系数a0,a1,…as的值,然后根据方程(9)和方程(10),可得出方程(5)的精确行波解.

2.2 方程(1)的精确行波解

根据方程(1)与方程(5)解之间的关系,先用辅助方程法对方程(5)的精确行波解进行研究.假设方程(5)有解形如

(11)

在方程(5)中,由于wξξ与w2的平衡原则,n+2=2n可得n=2,从而方程(11)可变为

w(ξ)=a0+a1F(ξ)+a2F2(ξ).

(12)

利用方程(10)和方程(12)可计算出

(13)

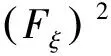
(14)

把方程(12～14)代入方程(5)合并同类项,令Fmξ(m=0,1,2,3,4)的系数等于0,得到关于a0,a1,a2的代数方程组为

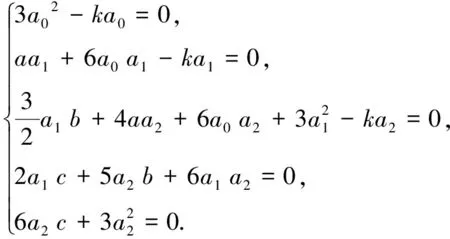
(15)

经计算可得方程组(15)的解有以下3种情形:

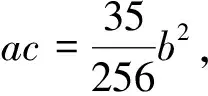
(16)

其中τ=1或者0.

情形2 当k=±a,c=0,有

(17)

其中τ=0或者1.

情形3 当k=±4a,b=0,有

(18)

其中τ=0或者1.

根据a0,a1,a2的解(16),以及(12)和方程(10)的精确解可知:

定理1 若波速k=±a,a,b,c为任意参数且满足256ac-35b2=0,ε=±1,Δ=b2-4ac,则方程(1)的16个精确行波解为:

1)当a>0时,

(19)

(20)

2)当a>0,Δ>0时,有

(21)

3)当a<0,Δ>0时,有

(22)

(23)

4)当a>0,c>0时,有

(24)

(25)

5)当a>0时,

(26)

注:1)表达式(19～26)中,“+”时,τ取0,“-”时,τ取1.

2)文献[9]的解(24)可以作为本文解(26)的一个推论.

根据a0,a1,a2的解(17),以及(12)和方程(10)的精确解可知:

定理2 若波速k=±a,a,b为任意参数,ε=±1,Δ=b2-4ac,则方程(1)有如下2个钟状孤波解和10个有界行波解:

1)当a>0时,有

(27)

(28)

2)当a>0,Δ>0时,有

(29)

3)当a<0,Δ>0时,有

(30)

(31)

4)当a>0时,有

(32)

需要注意几点:

1)表达式(27～32)中,“+”时,τ取0,“-”时,τ取1.

2)τ取0时,钟状孤波解(27)变为

(33)

钟状解(32)对应着图2中的同宿轨.

3)τ取1时,钟状孤波解(27)变为

(34)

钟状解(33)对应着图1中的同宿轨.

4)文献[9]的解(21)可以作为本文结论(32)式的一个推论.

根据a0,a1,a2的解(18),以及(12)和方程(10)的精确解可知:

定理3 若波速k=±4a,a,c为任意参数,ε=±1,则方程(1)有如下4个有界行波解:

1)当a>0时,有

(35)

2)当a>0,b=0时,有

(36)

其中，表达式(35～36)中,“+”时,τ取0,“-”时,τ取1.

文献[9]的解(18)可以作为本文结论(36)式的一个推论.

3 结语

本文利用辅助方程法求解了(1+1)维积分微分Ito方程,成功地得到了2个钟状孤波解和若干新的有界行波解精确表达式,而且文献[9]中的结论可以作为本文结论的推论.