基于数形结合思想的初中数学教学策略探究
湖北省南漳县城关镇胡营中学 张鸿飞
一、运用数形结合思想的意义
数形结合思想的运用需要注意以学生为主体,以培养学生数学思维为基础,满足新课程改革对现代教育提出的要求。数形结合在教学中要结合数学实例向学生讲解渗透,加强学生对数学的重视程度,培养学生的数学素养以及能力。数形结合方法体现在数学的各种题型中,考查学生对数学的理解,所以在数学教学中,让学生深入理解并且掌握数形结合是非常重要的。
数形结合可以培养学生的多方面能力,例如学生在多次运用图形解题之后,再遇到类似题目时,便会在大脑中形成自己的直觉,较快地反应出题目对应的图形,省去了一步一步的分析,节约了做题时间。例如很多函数的学习是很抽象的,在加入图象之后,可以帮助学生理解函数这样抽象的概念,锻炼学生的抽象思维。再例如在平面向量的学习中可以加入图形,让学生在理解平面向量的基础上向空间向量延伸,培养学生的发散思维。
二、数形结合思想下的初中数学教学策略
1.集合问题
例题:某班级中有男生共63个人,其中喜欢打网球的有35个人,喜欢打篮球的有27个人,两项运动都喜欢的有5个人,那么这两项运动都不喜欢的有几个人呢?我们运用数形结合解决本道集合问题时,可以利用韦恩图,如下图所示,用图中的小圆形代表喜欢打篮球的27个人,大圆形代表喜欢打网球的35个人,两个圆形交集的地方代表喜欢这两项运动的5个人,则除去已知人数的图形部分,阴影部分就是这两项运动都不喜欢的人数。计算如下:63-(35+27-5)=6(人)。

在数学集合问题中,如果学生只靠单纯地运算是很容易多加(减)、漏加(减)的,但是数形结合的运用能够将题目中的已知条件直观地表现出来,这样就使学生的思路非常清晰,减少运算错误,而且运用图形解答此题,也会降低这类题型的难度,让学生更容易理解集合问题。
2.函数问题
在初中教材一元二次方程的讲解过程中运用数形结合思想,一般地,当a>0(a<0)时,则方程y=ax2+bx+c的图象是一条开口向上(下)的抛物线,此时的图象具有最低(高)点,当x=-时,方程y=ax2+bx+c具有最小(大)值y=。
例题:根据y=ax2+bx+c(a≠0)的图象(如下图),回答下列问题:①写出方程ax2+bx+c=0的两个根;②写出y随x的增大而减小的自变量x的取值范围。
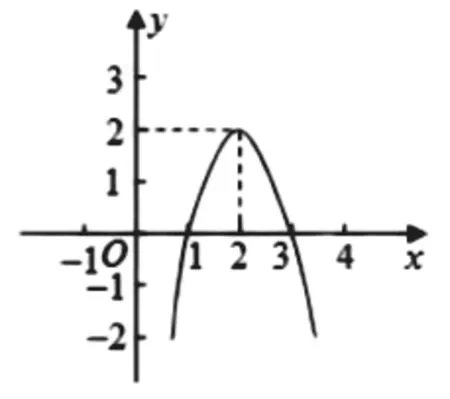
根据数形结合思想,图象可知,①使方程成立的两个根为x1=1,x2=3;②y随x的增大而减小的图象在对称轴的右侧,所以自变量的取值范围为x>2。
由此可知,在函数问题中加入数形结合思想是将抽象的函数知识转化为直观的图象,便于学生的记忆与理解,也能在做题时帮助学生简化问题,让学生更容易理解函数问题。
3.几何问题
例题:已知一条直线过点(-3,0),求当这条直线l与单位圆有两个交点的时候,这条直线l的斜率k的取值范围。根据题意,我们可以结合数形结合思想画出这条直线与单位圆相交的图象,如下图所示,此时我们可以求出过点(-3,0)的两条直线的斜率,,所以可得出k的取值范围为-。
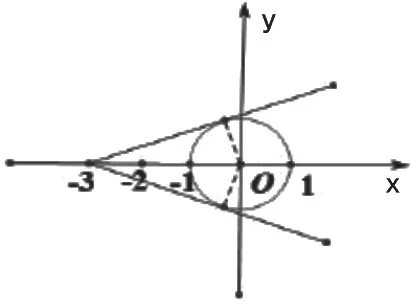
在几何问题中运用数形结合思想即将抽象的几何图案用直观的图象表示出来,便于学生理解距离、斜率等问题,也可使复杂的几何问题简单化,以此增加学生解决数学问题的信心,也可激发学生学习数学的兴趣,培养学生的数学思维。
总之,数形结合思想在初中数学教学中的应用,可以将复杂变简单、抽象变直观,在很大程度上帮助学生提升数学思维,所以,老师要加强对数形结合思想的重视,在教学中将数形结合灌输到学生的大脑中,以此增加学生的信心,提高学生的学习成绩与解决数学问题的能力。但是,并不是所有的问题都可以运用数形结合思想,老师一定要注意,不能让学生将数形结合作为解决一切数学问题的万能钥匙,要懂得灵活运用,才能在此基础上更好地发展。

