初中数学教学中的假探究及解决策略
熊诵财

修订后的《新课标》中,对于课程目标提出了二维目标:结果目标和过程目标。其中,过程目标使用“经历”“体验”“探索”等行为动词表述,而总目标也提到:“通过义务教育阶段的数学学习,学生能:获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”“有利于学生体验与理解、思考与探索。”由此可见数学探究活动在数学教学中的重要地位与作用。因此,作为数学课标载体的数学教材,在内容的编排上,也很好地反映了新课标的精神,具体体现就是教材加大了探究活动的份量,特别是几何知识的探究。
广大教师在学习、理解、贯彻实施新课标的过程中,积极开展课堂教学的探究活动,精心设计、积极组织,使学生在数学学习活动中,能够动脑、动手,有效开展小组合作学习等学习活动,对于丰富和发展学生的数学思维能力、推理能力起到了一定的作用。但是,由于不同教师对于探究活动的认识不同,开展探究活动的教学设计、组织、实施能力也各有高低,客观上导致部分教师在平时的教学过程中,会产生一些貌似探究活动,实为假探究的教学活动。
所谓假探究,是指师生在探究过程中,只是将探究活动停留在表面的形式上,学生的思维活动很少或根本得不到训练,所得到的结论不是在探究活动中得到,而是通过课前的预习或课堂上老师的引导、讲评乃等方式而得到。
一、假探究案例分析
本人在一些听课教研活动中,时常会听到一些实为假探究的教学观摩课。现举几例加以说明。
案例1. 表面上的探究,内容的可操作性不强。
例如,人教版教材八下18.1《勾股定理》的教学中,
一位教师是如此进行探究活动的教学设计的:
环节1.纸板能穿过门框吗?
环节2.探究等腰直角三角形三边数量关系.
如图1,在环节1中,教师展示出两个模型后,问学生:“纸板能否穿过门框?”学生异口同声地回答:“能!”然后再开始实验活动。
如图2,在环节2中,教师引导学生从图形的面积入手,得出三个图形之间的面积关系:
2(个单位面积)+2(个单位面积)=4(个单位面积)
以上的探究活动,学生都是在预习的基础上开展的,所以环节1根本没有任何探究的实质成分,只是教师表面的作秀,是真正的假探究。环节2的探究活动也是在教师的强烈提示或暗示下,学生得出“2+2=4”(实际上,2×2=4也成立啊!)。
案例2. 看似探究,实为演示。
在人教版教材九上25.1.2《概率》的教学中,老师为了让学生了解不同事件的概率情况,设计了如下的探究活动:在一个一面透明,其它各面都密闭的箱子里,放有3个红色乒乓球,6个绿色乒乓球,老师在自己看不到箱子中球的情况下,每次从箱子里随机地摸出一个球,然后再放回,每次记录好球的颜色。经过多次的实验后,老师引导同学们计算出摸到红球次数和绿球次数大约占总次数的几分之几,然后问学生:“摸到红球的概率是多少?”“摸到绿球的概率是多少?”同学们争先恐后地回答:“三分之一!”“三分之二!”老师很高兴地说:“同学们真聪明!回答得很好!”
以上探究活动中,学生对二种不同事件的概率,已从透明的窗口中看得清清楚楚,早已心中有数,教师的摸球活动根本没有一点实质的探究效果,学生根本不能从中去加深对“概率”这一概念的理解。
二、解决策略
假探究表面热闹,实则毫无教学效果,浪费宝贵的教学时间,因此教师在准备探究活动的教学设计时有必要分清楚什么是真正、有效的探究活动,认真设计、组织和实施,使探究活动真正发挥它的作用。
1.创设良好的探究氛围
一个好的探究活动的设计,能够吸引学生一步步地去展开探究活动。如在中点四边形的教学内容中,学生通过课本内容的学习,已经了解了关于中点四边形的基本知识,但很多学生对于这些知识的理解只是停留在表面现象上,对以上知识的学习也只是靠死记硬背。能否在教学中有所突破呢?教师可尝试让学生进行如下的探究活动:
步骤1.(如图5-1),画任意一个四边形ABCD,再画出它的中点四边形EFGH。四边形EFGH是什么特殊的四边形?
步骤2.(如图5-2),画一个对角线互相垂直的四边形ABCD,再画出它的中点四边形EFGH。四边形EFGH是什么特殊的四边形?
步骤3.(如图5-3),画一个对角线相等的四边形ABCD,再画出它的中点四边形EFGH。四邊形EFGH是什么特殊的四边形?
步骤4.(如图5-4),画一个对角线互相垂直且相等的四边形ABCD,再画出它的中点四边形EFGH。四边形EFGH是什么特殊的四边形?
步骤5. 你也能构造一个中点四边形是某一个特殊四边形的四边形吗?试试看!
通过以上的探究活动,学生们都会对中点四边形有一个全面的了解,知道矩形、菱形、正方形的中点四边形之所以特殊,并不是因为矩形、菱形、正方形它们本身很特殊,而是因为它们分别具有了对角线相等和互相垂直的性质。所以学生们在进行了前四个步骤的操作探究后,学习的热情会更高,会构造出不同的四边形出来,整个探究活动也会收到很好的效果。
2.选择合适的探究内容
并不是所有的教学内容都适合开展探究活动的,教师在开展探究活动时,一定要根据自己学生的情况,选择合适的探究内容及开展探究活动的方式和步骤,使得学生能够通过探究活动,有效地提高对数学问题的发生、发展过程的理解,体会和感悟获取数学知识的方法和思想。
如在等腰三角形“三线合一”性质的教学中,教师可尝试进行如下的探究活动:
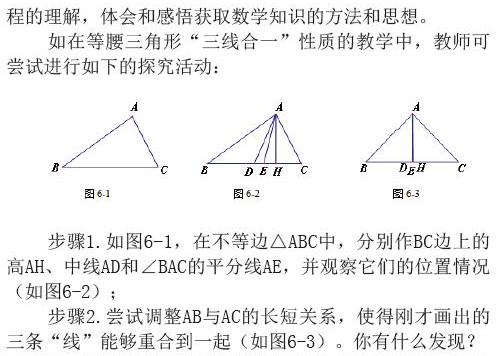
步骤1.如图6-1,在不等边△ABC中,分别作BC边上的高AH、
中线AD和∠BAC的平分线AE,并观察它们的位置情况(如图6-2);
步骤2.尝试调整AB与AC的长短关系,使得刚才画出的三条“线”能够重合到一起(如图6-3)。你有什么发现?
通过以上设计,学生在步骤1很容易完成任务,比较有信心和兴趣去进行进一步的探究活动,所以纷纷投入下一步骤的探究活动中去。通过进一步的尝试、探索,很多同学都能得出正确的结论,整个探究活动会收到较好的效果。
3.精心组织和指导探究活动
探究学习强调学生的主体学习地位,但不是不要教师指导,教学中教师要承担起管理和调控的职能。教师在指导学生开展探究活动的过程中,要注意克服二种极端倾向:一是置之不理型。二是指导过度型。有些教师一方面想搞探究式教学,另一方面又怕学生不会探究,于是就在学生探究之前设置解决问题的“路标”,学生一走“弯路”时马上就可以得到提醒或暗示,使得学生的探究活动只是停留在表层,缺乏深层的思维训练,学生的数学思维能力并没有得到提高。
探究性教学可以有效地提高学生提出问题、观察问题、思考问题以及解决问题的能力,不仅可以使学生加深对知识技能的理解与掌握,还有利于创新思维与创新能力的形成和发展。在此过程中,能否取得成效的关键是,学生在学习过程中的主体地位是否能得到充分的体现。换言之,探究性教学的成功实施涉及两个方面——既要充分体现学生在学习过程中的主体地位,又要重视发挥教师在教学过程中的主导作用,离开其中的任何一方,探究性学习都不可能有良好效果。

