基于赫—巴模型的微小井眼钻井连续油管内钻井液流阻计算分析

侯学军 金 锐 宋洪奇 张 辉 王郑库 高 鹏 房 军

1.重庆科技学院石油与天然气工程学院 2.中国石油大学石油工程教育部重点实验室3.中国石油集团川庆钻探工程有限公司川东钻探公司

0 引言

微小井眼[1]连续油管（CT）钻井技术[2-3]是一种前沿钻井技术，微小井眼CT钻井技术因作业简单、作业费用低、占地面积小、污染小和储层伤害小等优点而引起了国内外的广泛关注[4]。微小井眼CT钻井井眼尺寸小，导致钻井液流动空间小，排量较小，返速较高，循环损失较大，限制了微小井眼CT钻井的推广使用。为解决微小井眼CT钻井循环钻井液流阻过大的问题，国内外学者做了很多的研究：2000年Medjani和Shah[5]预测了非牛顿流体在CT中循环钻井液流阻；Willingham和Shah[6]对滚筒上和井筒中的CT使用牛顿流体和非牛顿流体的流阻压耗进行了研究；Shah等[7-8]先后对CT钻井岩屑对循环压耗的影响进行研究，并预测CT压裂循环压耗。国内侯学军等[9-11]通过建立CT滚筒的模型，使用幂律流体计算滚筒上和井筒中CT内循环压耗；李荣等[12-13]总结了适合常规井眼计算压耗的赫—巴模型；汪友平等[14]研究了圆管中赫—巴流体结构流流动规律并建立了速度分布、流量、平均速度、压降和雷诺数的计算公式；国内外关于使用赫—巴模型进行CT钻井循环压耗的计算实例很少，大多只是在理论阶段。

赫—巴流变模型是经过多年的大量实验和理论研究并结合油田现场实际得出的三参数流变模式，其能够反映大多数钻井液所具有的屈服应力和剪切稀释的特点，在特定的情况[15]下能够反映牛顿液体、塑性液体、幂律液体的特性，精度较高，在各大油田广泛使用。因此选用赫—巴模型，对微小井眼钻井CT内钻井液流阻进行定量的计算分析，研究影响微小井眼钻井CT钻井液流阻的因素和相应的控制方法，优化减小内钻井液流阻，推动微小井眼CT钻井技术的发展。

1 赫—巴模型

赫—巴模型的流变方程[16]为

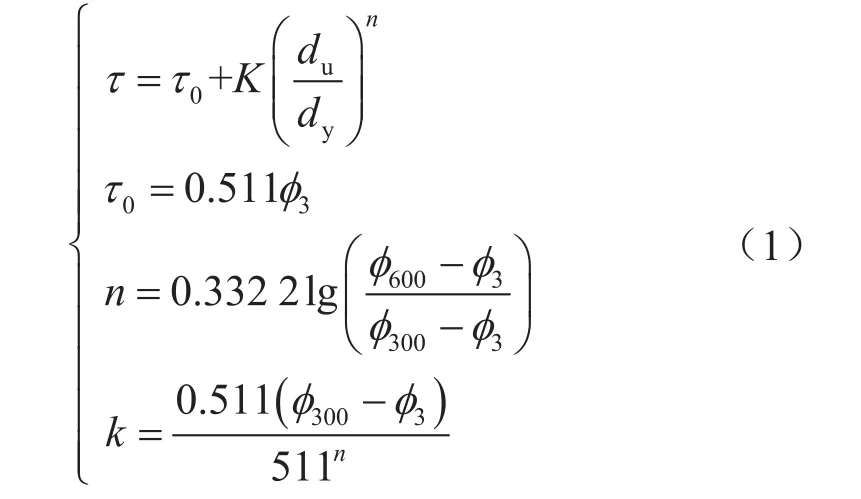
式中τ表示剪切应力，N/m2；τ0表示屈服切应力，N/m2；K表示稠度系数，N·sn/m2；du/dy表示剪切速率，s－1；n表示流变指数，无量纲；600、300和3分别表示旋转黏度计在600 r/min、300 r/min和3 r/min下的读数。

2 赫—巴模型流变参数计算

2.1 雷诺数计算

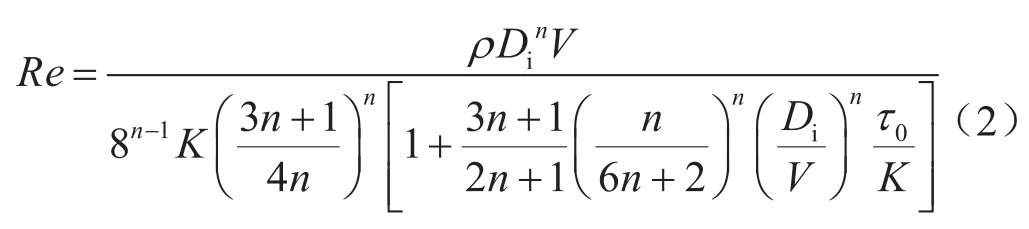
式中Re表示雷诺数，无量纲；ρ表示钻井液的密度，kg/m3；Di表示CT的内径，mm；V表示钻井液的流速，m/s。

2.2 滚筒上CT内钻井液流阻计算

假设判别因子C1和C2，通过比较雷诺数与C1和C2的大小，判断赫—巴流体的不同流动状态以及对应的摩阻系数[17]计算式为：

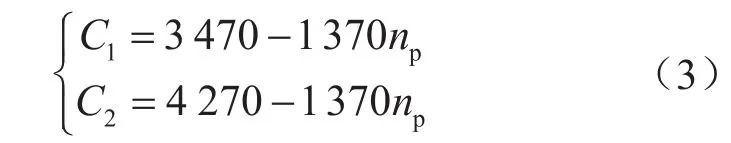
式中np表示管内赫—巴流体流变指数，无量纲。

根据迪恩数[18-19]和雷诺数的相互关系，滚筒上CT内钻井液循环流阻在不同流态下的范宁摩阻系数[15]计算公式为：

式中fi表示微小井眼作业滚筒上第i层CT内流体处在不同流态下对应的范宁摩阻系数；NDn表示迪恩数，无量纲；a、b分别表示计算系数。

根据范宁方程，滚筒上CT内钻井液流阻计算模型为：

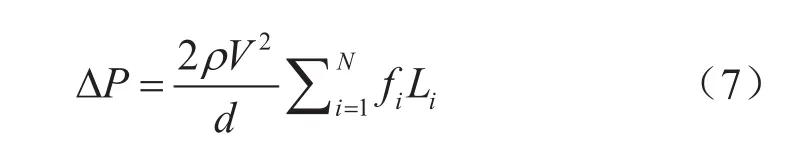
式中ΔP表示赫—巴流体在滚筒上的CT内钻井液流阻，Pa；d表示CT内径，mm；Li表示缠绕在滚筒上的第i层CT的长度，m。

2.3 井筒中CT内钻井液流阻计算

假设判别因子K1和K2，通过比较雷诺数与K1和K2的大小，判断赫—巴流体的不同流动状态以及对应的摩阻系数计算公式为

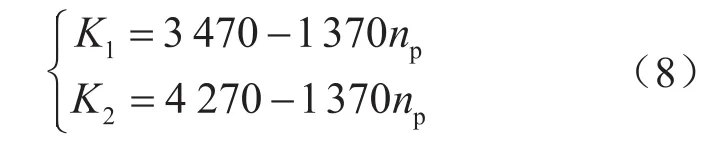
根据雷诺数和摩阻系数的相互关系，井筒中CT内钻井液流阻在不同流态下的范宁摩阻系数计算公式为：

式中f表示微小井眼作业井筒中CT内钻井液处在不同流态下对应的范宁摩阻系数，无量纲。

根据范宁方程，井筒中CT内钻井液流阻的计算模型为

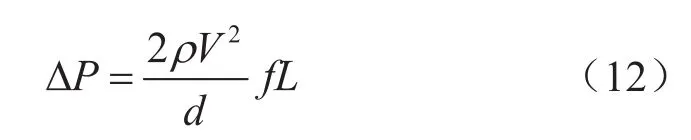
式中L表示井深，m。

3 CT内钻井液流阻计算结果分析

3.1 计算参数设定

根据在Ø89 mm的微小井眼中可用CT（表1），选择不同直径CT管柱及其对应的CT管柱滚筒的计算参数（表2），假设钻井液密度为1.50 g/cm3，600为35 mPa·s、300为 12 mPa·s、3为 2 mPa·s，CT钻井的深度[20-22]一般介于2 000～3 500 m，所使用的CT外径一般介于12.7～114.3 mm，但在钻井作业中，适合采用外径大于44.450 mm的连续油管[23]。对Ø89 mm的微小井眼CT内钻井液流阻进行计算并分别绘图（图1～3）。

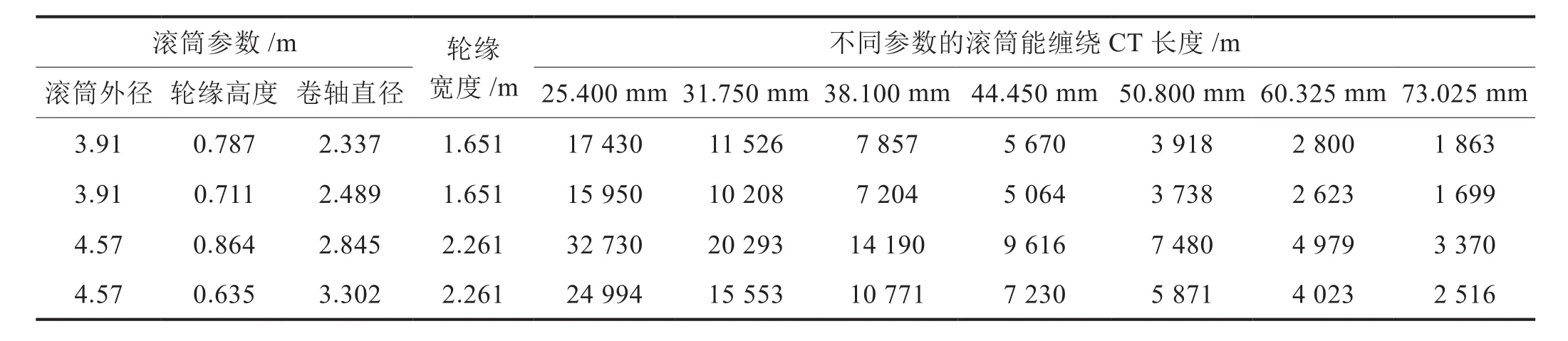
表2 不同CT外径滚筒缠绕CT长度参数表[25]

表1 CT参数表[24]

3.2 计算结果分析

对滚筒上2 000 m和井筒中2 000 m的CT内钻井液流阻随流速变化计算结果如图1所示，计算结果表明，①随着流速的增加，CT内钻井液流阻均呈线性增加。②滚筒上的CT内钻井液流阻要比井筒中CT内钻井液流阻大很多，滚筒上CT内钻井液最大流阻为51 MPa，而井筒中CT内钻井液最大流阻仅为5.6 MPa，且随流速增加，滚筒上的流阻增加的幅度要比井筒中的流阻增加的幅度大。

当钻井液流速为1.5 m/s和2.0 m/s时，CT内钻井液流阻随管长变化规律如图2所示，计算结果表明，①滚筒上和井筒中CT内钻井液流阻都随着管长的增加呈线性增加。钻井液流速为1.5 m/s、2.0 m/s时，滚筒上CT内最大钻井液流阻分别为51 MPa、76 MPa（图2-a、c）；井筒中的CT内最大钻井液流阻分别为5.6 MPa、8.4 MPa（图2-b、d）。②当微小井眼CT钻井时，滚筒上的流阻特别大，在满足钻井的条件下，尽量减小钻井液循环流速，以降低滚筒上CT内钻井液流阻。

随CT内径变化，钻井液流阻规律如图3所示，计算结果表明：①滚筒上和井筒中的CT内钻井液流阻都随着CT内径的增加先呈加速度减小，至内径为50 mm CT后直线减小；②滚筒上的CT内钻井液流阻最大为36 MPa，井筒中CT内钻井液流阻最大为3.9 MPa，滚筒上的流阻比井筒中的流阻大很多，因此当满足钻井的最小携岩流速下，可使用大管径的CT管柱进行作业，降低滚筒上的CT内钻井液流阻。

随滚筒直径变化，Ø73.025 mm CT内钻井液流阻变化规律如表3所示，计算结果表明：①随着卷轴直径的增加，绕轴上CT流阻相应的微量增加，基本可忽略，因此，CT滚筒的选择主要考虑滚筒载荷、CT最小弯曲半径和运输的体积高度；②滚筒上CT内钻井液流阻的大小，主要是随着钻井液流速的增大而增大，因此在使用CT钻井时，在满足正常钻进的条件下，减小钻井液的流速，降低滚筒上的流阻，以保证循环流阻不超过地面最大泵压。

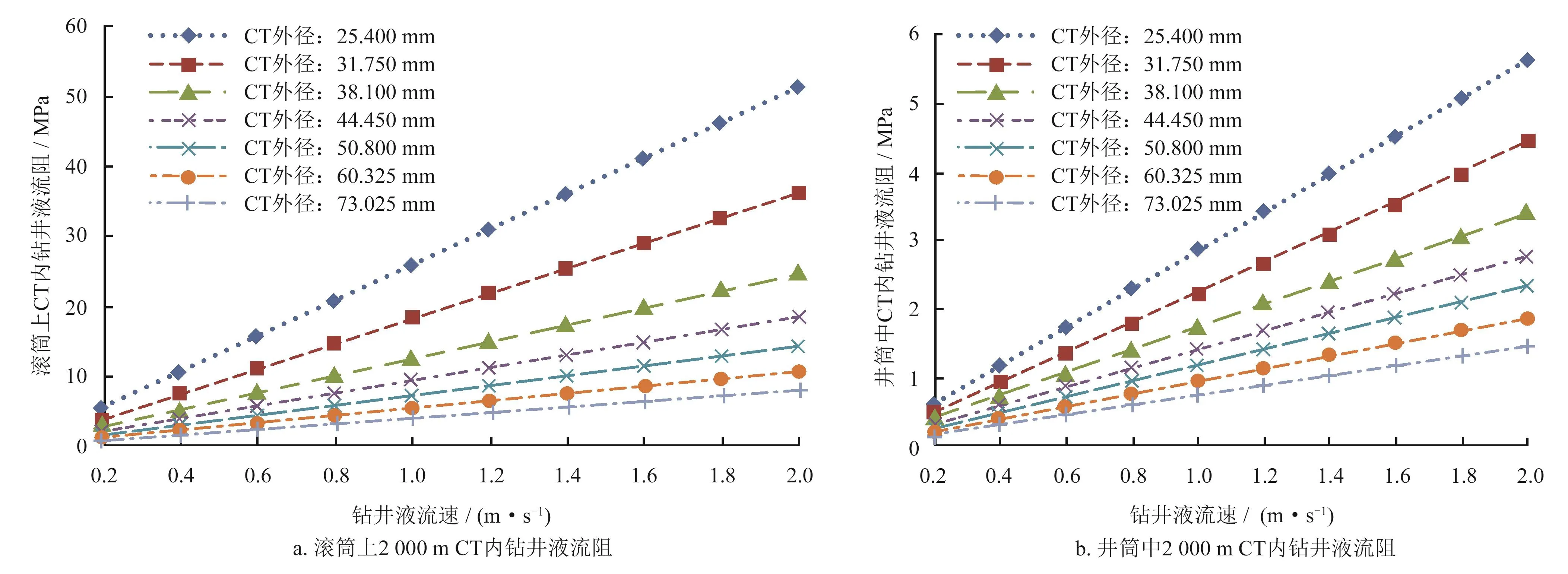
图1 CT内钻井液流阻随钻井液平均流速变化曲线图

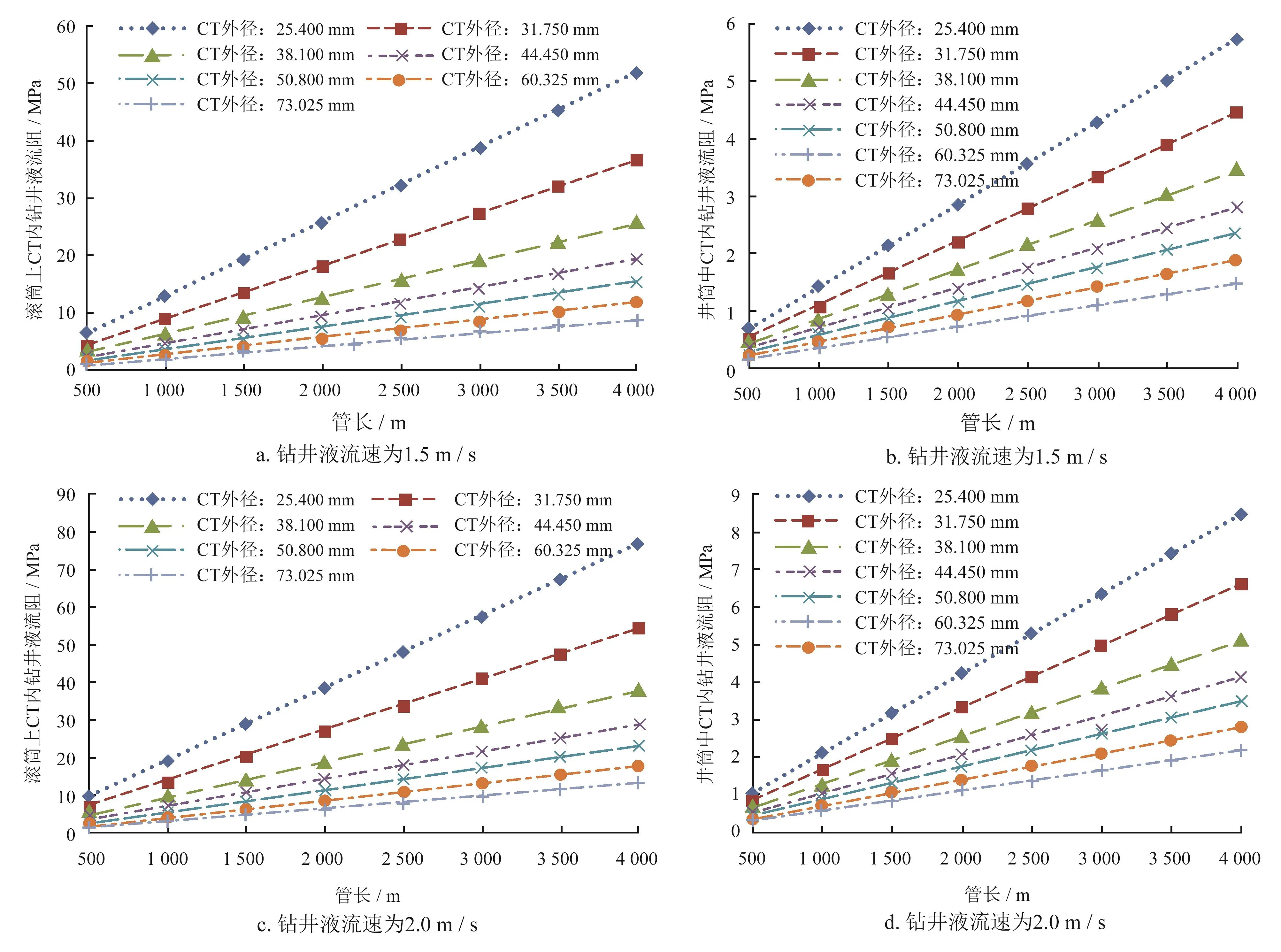
图2 滚筒上和井筒中CT内钻井液流阻随管长变化曲线图

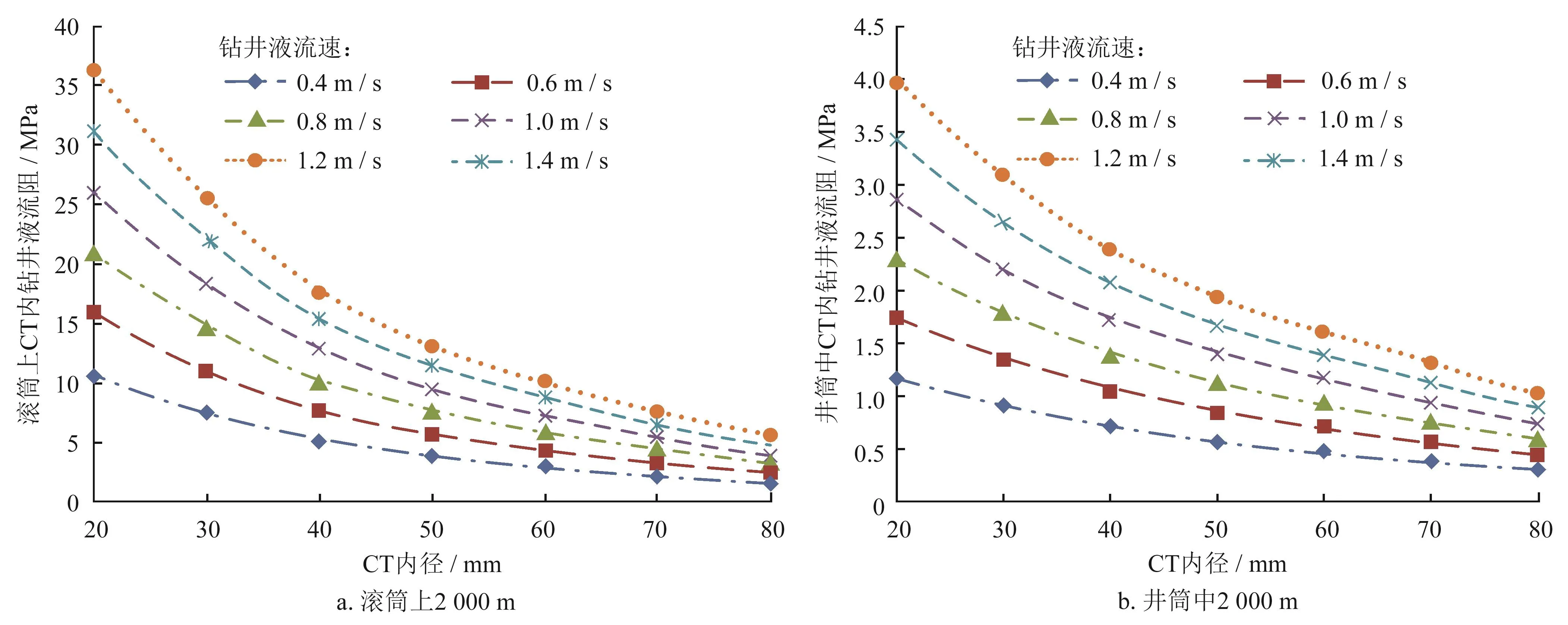
图3 CT内钻井液流阻随CT内径变化的曲线图

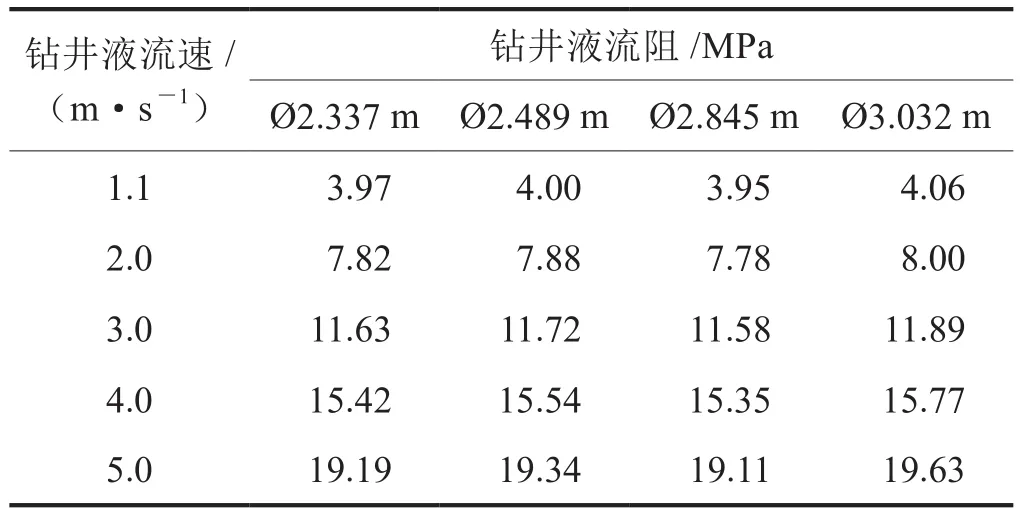
表3 CT内钻井液流阻随滚筒卷轴直径变化表

CT内钻井液总流阻随滚筒上CT长度变化规律如表4所示。计算结果表明：①当滚筒上分别缠绕4000 m的不同直径的CT进行井下作业，随着CT不断地注入微小井眼中，滚筒上的CT长度从4000 m不断减少到0 m，CT内钻井液流阻呈直线下降，循环最大总流阻出现在CT全部缠绕滚筒上，循环最小总流阻出现在井底；②在CT内循环流速1 m/s时，随内径越小，CT内钻井液总流阻越大，Ø73.025 mm～Ø44.500 mm的4 000 m长的CT内钻井液总流阻没有超过25 MPa；如CT内循环流速提升至1.5 m/s时，Ø73.025 mm～Ø50.800 mm CT内钻井液总流阻没有超过25 MPa，地面泵压基本可以满足正常钻进。因此，为减小CT内钻井液总流阻，可使用内径较大的管径（Ø50.800 mm～Ø73.025 mm）进行钻井作业，当使用的CT管径一定时，在满足最小携岩的流速下，可适当地降低循环钻井液的流速，降低CT内钻井液流阻，使钻井作业正常进行。

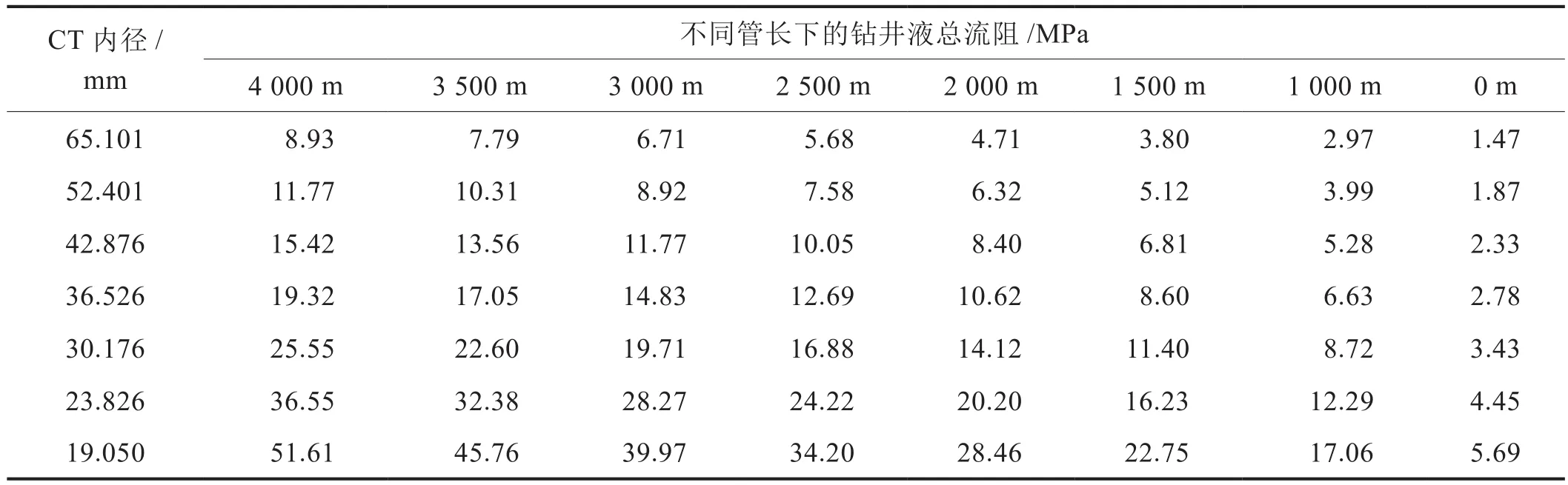
表4 CT水眼内循环流速1 m/s时的钻井液总流阻随管长变化表

3.3 CT钻井参数优选

通过计算可知在钻井作业中，最小的环空携岩钻井液流速[26]为0.54 m/s，使用微小井眼CT钻井，地面泵组的额定泵压加高，一般为30～40 MPa。CT钻井的最大深度可达到4 500 m，在钻井中现场多使用外径44.450 mm的CT[23]。因此，假设使用4000 m CT进行微小井眼（Ø89 mm）钻井，计算微小井眼CT内钻井液流阻，选择合适钻井的管径和循环钻井液的流速，计算结果和分析如下：

由表5可知：①外径50.800 mm CT钻井时，推荐使用钻井液流速介于1.5～2.0 m/s；②外径60.300 mm CT钻井时，推荐使用的钻井液流速介于1.5～2.5 m/s；③外径73.100 mm CT钻井时，推荐使用的钻井液流速介于1.5～3.0 m/s。

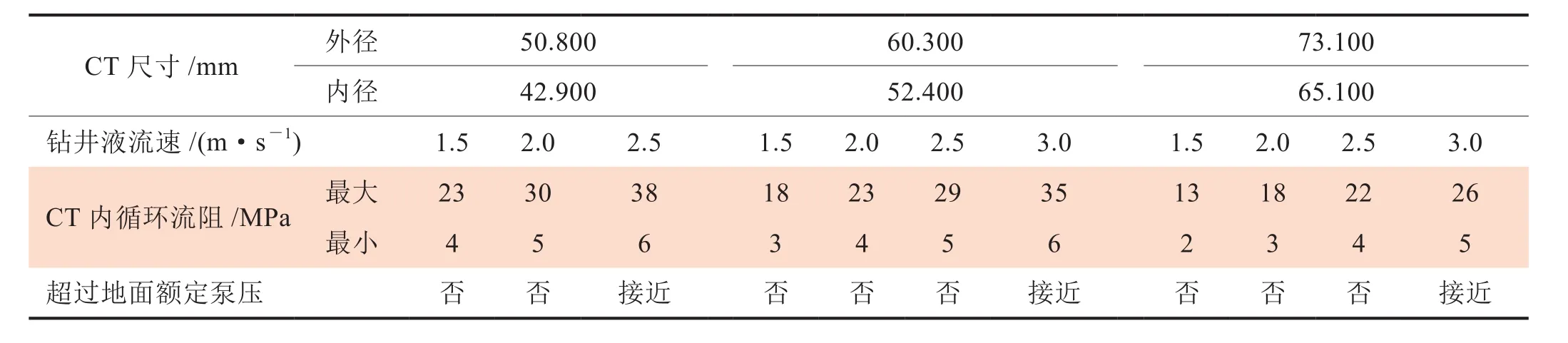
表5 钻井液流速优选表

4 现场应用与实例对比分析

根据长江大学关于连续油管流阻模拟的实验数据[27]：使用赫—巴模型计算42 m长，外径25.4 mm（内径19.05 mm）的CT在循环清水时的流阻与实验数据进行对比分析，如图4所示。由图4可知，当CT缠绕在滚筒上时，循环钻井液的流速介于1.1～3.6 m/s时，计算值与实验数据误差范围介于3.3%～9.7%，当流速2.3 m/s时，误差最大，达9.7%，如图4-a所示。当CT都位于井筒时，循环钻井液的流速介于4.4～5.6 m/s时，计算值与实验数据误差范围介于3.3%～14.8%，当流速5.6 m/s时，误差最大，达14.8%，如图4-b所示。通过对比计算值与实验值的相对误差可知使用赫—巴模型计算微小井眼CT内钻井液流阻的精度较高，能够满足使用。

东北某油田使用外径60.325 mm CT进行老井开窗侧钻，井深2 380 m，侧钻井段为1 500～2 380 m，使用的钻井液密度为1.25 g/cm3，钻井排量介于7～10 L/s，地面额定泵压介于16～27 MPa。因此，使用赫—巴模型对该井CT钻井时进行CT内钻井液流阻计算和分析，计算结果如表6所示。

由表6可知，使用赫—巴模型计算值与现场实测值之间的误差介于3.1%～8.9%，表明使用赫—巴模型计算微小井眼钻井CT内钻井液流阻是完全符合实际应用的。

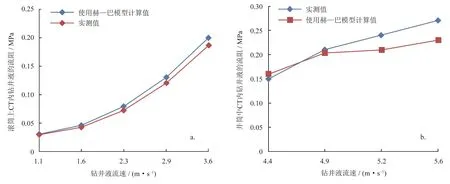
图4 采用赫—巴模型分别计算滚筒上（a）与井筒中（b）CT内钻井液的流阻同实测值对比图

5 总结

1）结合微小井眼CT钻井的特性，使用赫—巴模型，计算微小井眼钻井CT内钻井液流阻，分析CT内流阻随钻井液平均流速、CT长度、井深、CT内径和滚筒直径等参数从定性到定量的变化规律，探索减小微小井眼CT内循环流阻的方法

2）根据计算结果，分析影响微小井眼CT钻井内钻井液流阻的主要因素，总结控制微小井眼钻井CT内钻井液流阻的相应方法：当钻深井时，滚筒上缠绕的CT比较长时，可使用几个相同直径的滚筒进行缠绕，以减小滚筒上CT内钻井液流阻；使用大管径的CT进行钻井，降低CT内钻井液流阻；在满足正常钻进条件下，减小循环钻井液的流速等。

3）通过计算在满足最小携岩流速下，使用不同管径钻井达到4 000 m时的CT内钻井液流阻，进行与地面额定泵压对比分析，优选适合微小井眼钻井的CT管柱以及推荐此管柱钻井时可使用的钻井液流速范围。

4）通过使用赫—巴模型计算值与实验数据和现场应用实例数据进行对比分析，明确使用赫—巴模型对微小井眼钻井CT内钻井液流阻进行计算能达到精度要求，满足现场的应用，促进微小井眼CT钻井技术发展。

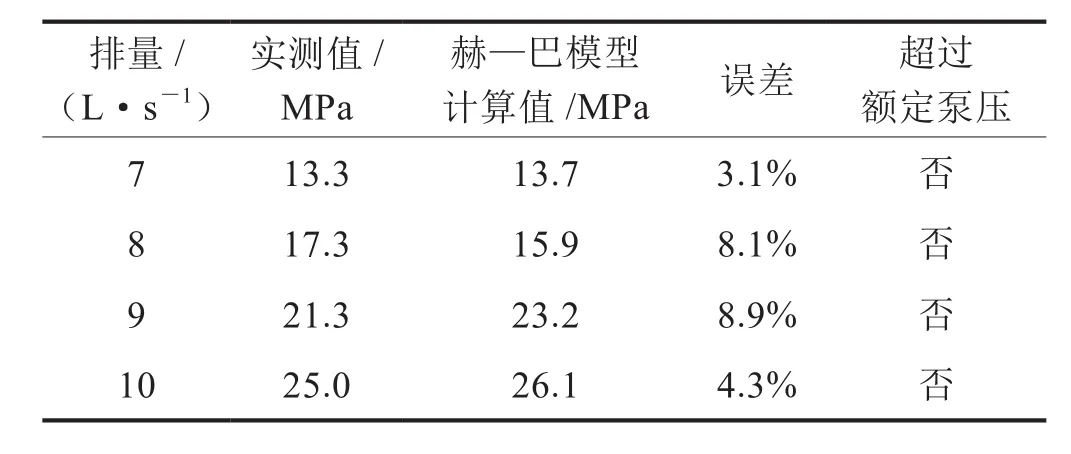
表6 东北某油田某井CT内钻井液流阻实测值与计算值对比表