提高页岩含气量测试中损失气量计算精度的解吸临界时间点法

刘 刚 赵谦平 高 潮 姜 磊 孙建博 刘 超

1. 陕西延长石油（集团）有限责任公司研究院 2. 陕西延长石油（集团）有限责任公司油气勘探公司

0 引言

目前主要通过在目的层取心、对岩样进行解吸测试后计算获得页岩含气量[1-3]，但在常规取心过程中因取心筒密闭性较差，气体逸散严重，该部分损失气量无法直接测得，而密闭取心因成本过于昂贵，其广泛应用受到限制[4-6]，由此对页岩含气量的准确评价造成较大的困难。由于煤层气在气体吸附解吸机理、扩散规律等方面与页岩气较为相似[7-8]，当前针对页岩损失气量的评价基本借鉴煤层气的相关研究成果来获得[9-12]。然而，由于在储层埋深、气体解吸速率等方面存在较大差异，适合于煤岩损失气量的计算方法对于页岩是否适用仍有待探讨，若盲目套用往往会使页岩损失气量的计算结果产生较大误差，从而直接影响页岩含气量的准确评价，对页岩气勘探开发工作的部署产生较大影响。为此，首先对现有页岩损失气量的估算方法进行适用性评价，然后基于岩心上提过程中气体的扩散机理，提出了一种适用于页岩损失气量估算的解吸临界时间点法。结合鄂尔多斯盆地中生界上三叠统延长组长7段某口页岩气井的常规取心岩样的解吸实测数据，采用USBM法、多项式函数法及解吸临界时间点法计算页岩损失气量，进而得到页岩含气量。通过与该井同层位的保压取心岩样含气量测试结果进行对比，表明采用解吸临界时间点法可使页岩含气量的计算精度大大提高。

1 现有页岩损失气量估算方法的适用性

在岩心上提过程中，随着岩心温度变化，气体在岩心介质中的扩散规律并非一成不变，而是一个动态变化过程，本文将该过程划分为初期平衡扩散和后期非平衡扩散两个阶段。在初期平衡扩散阶段，岩心内气体解吸速率和扩散速率保持恒定，且气体的解吸和向外扩散能够达到一个相对平衡的状态，从而使得岩心内气体浓度能保持稳定；而在后期非平衡扩散阶段，随气体扩散时间延长，由于围压下降，裂隙、微裂隙和基质孔隙中赋存的气体开始大量逸散，而吸附于基质表面的气体解吸速度过慢，从而使岩心内气体浓度无法继续保持稳定。目前，针对初期平衡扩散阶段，页岩损失气量的计算方法包括USBM法[13-14]、修正的USBM法[15]等方法；针对后期非平衡扩散阶段，页岩损失气量的计算方法包括多项式函数法[16]、递减法[17]、分式函数法[18]等方法。本文主要探讨应用最为广泛的USBM法及多项式函数法的适用性。

1.1 USBM法

根据气体扩散原理，累计解吸气量与扩散时间满足式（1）[13-14]，在初期平衡扩散阶段，岩心脱离储层的时间较短，岩心温度变化并不明显，在该阶段气体扩散系数基本保持恒定，且同一岩心的原始总气量及特征扩散距离是不变的。因此，此阶段收集到的累计解吸气量与扩散时间平方根呈线性关系，将其线性趋势线外推到零时间点即得到损失气量。

式中G表示累计解吸气量，mL；GI表示原始总气量，mL；D表示气体扩散系数，cm2/min；r表示特征扩散距离，cm；t表示扩散时间，为损失气逸散时间和实测解吸时间的和，其中损失气逸散时间由岩心上提时间的一半和岩心装罐时间两部分构成，min；GL表示损失气量，mL。

1.2 多项式函数法

在后期非平衡扩散阶段，由于岩心温度明显下降，随时间延续气体扩散系数变小，导致扩散速度也变小，G与不再满足线性关系，根据曲线形态较多采用多项式函数进行计算[16]，即

式中a表示多项式函数的拟合系数；n表示多项式函数的最高次数。

1.3 适用性评价

四川、贵州等地龙马溪组海相页岩埋深一般都超过3 000 m，鄂尔多斯盆地延长组长7、长9段陆相页岩埋深也超过1 300 m，现场一次取心上提时间均超过4 h。以长7段页岩的常规取心为例，在上提期间岩心中气体大量逸散，岩心温度下降明显，到井口时已错过了初期平衡扩散阶段，此时收集到的数据（图1蓝色点）已呈现非线性关系，若采用USBM法计算，该数据点回归的线性趋势线斜率明显小于在初期平衡扩散阶段收集的数据点（图1红色点）回归的线性趋势线斜率，且前者外推得到的页岩损失气量也较低；而多项式函数法尽管能够较好地反映出筒岩心中气体的解吸情况，但该方法是依据后期非平衡扩散阶段的气体解吸动态而得，无法准确反映初期平衡扩散阶段的线性关系，且数据点回归趋势线的外推结果（图1绿色趋势线）也远大于实际损失气量。由此可见，上述损失气量计算方法应用在鄂尔多斯盆地延长组页岩损失气量的估算中均有较大局限性。

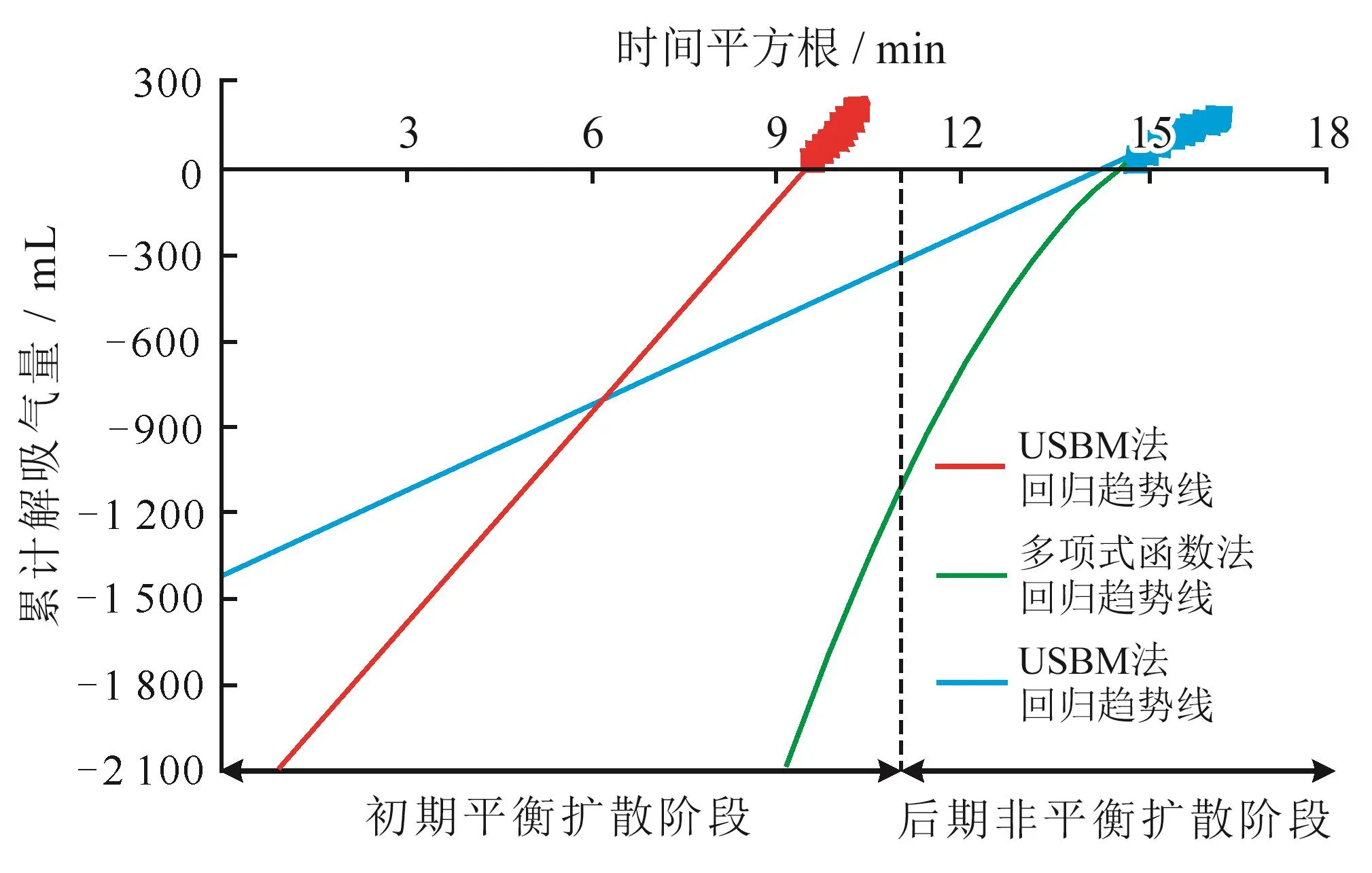
图1 USBM法与多项式函数法损失气量估算曲线图

2 解吸临界时间点法

前述计算方法导致页岩损失气量估算存在较大偏差的主要原因在于岩心上提时间过长，无法收集到初期平衡扩散阶段的解吸数据。但是，由于受到工程技术条件的限制，上提时间又很难大幅度缩短。为此，本文提出解吸临界时间点法来估算页岩损失气量。

2.1 解吸临界时间点的定义

如图2所示，在初期平衡扩散阶段不同时间点t1、t2将同一岩心上提到井口，解吸数据符合线性关系且斜率相同，反推得到的趋势线也相互平行；若岩心上提时间越长，能收集到的符合线性关系的数据就越少，直到某一时间点t0后收集到的数据点开始呈现非线性关系，该时间点t0即为解吸临界时间点；t0后为非平衡扩散阶段，该阶段内不同时间点t3、t4收集到的数据均呈现非线性关系，且对于同一岩心解吸曲线也相互平行。

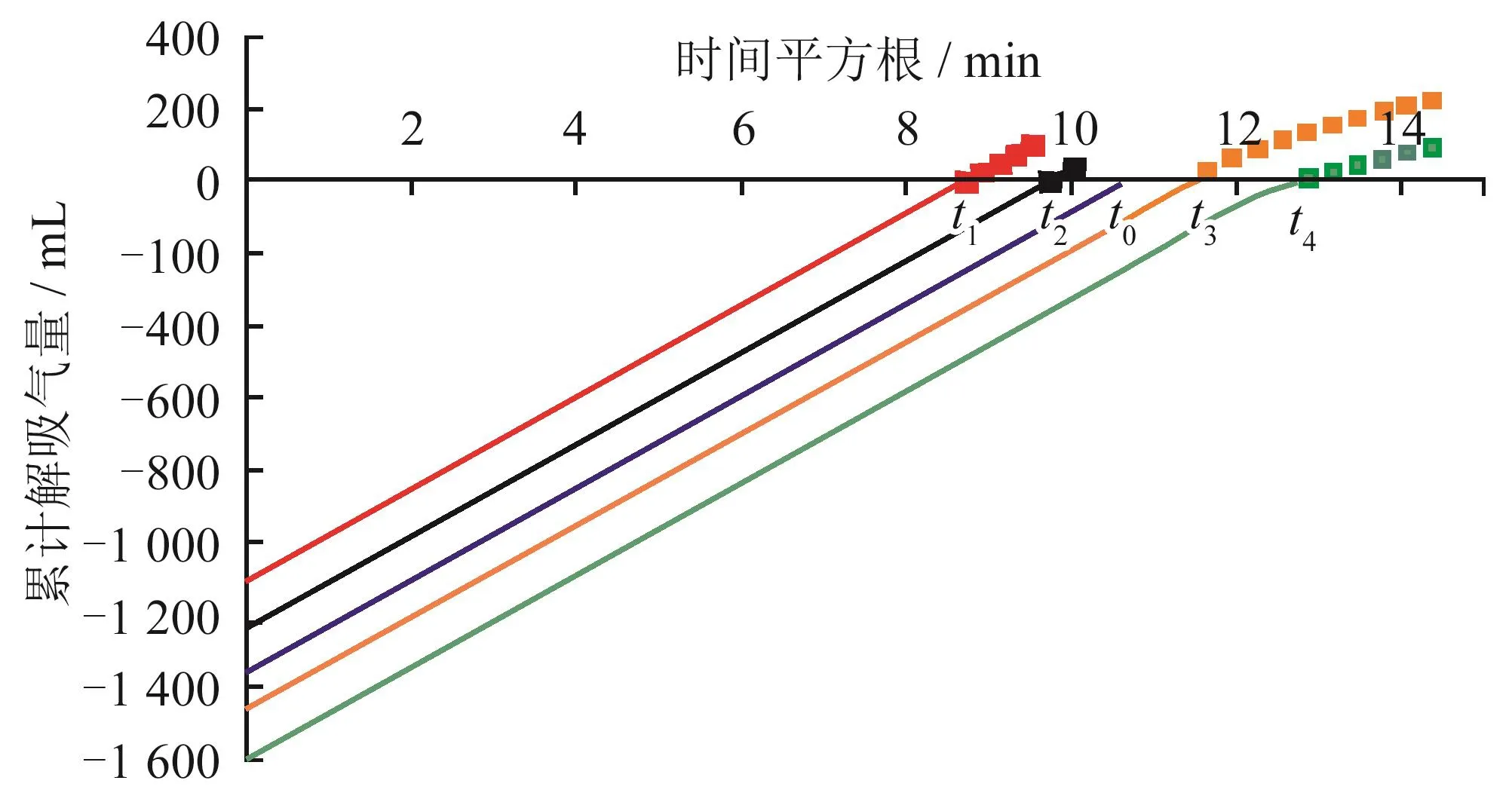
图2 不同时间点后的解吸曲线示意图

2.2 解吸临界时间点的确定

Bertard等[19]在1970年通过实验分析，证明气体释放速率与解吸时间前20%的平方根呈线性关系，因此页岩气解吸临界时间点可通过收集实际岩心的页岩气解吸数据来获得。对鄂尔多斯盆地延长组长7段实际页岩气井取心时间和现场解吸数据进行统计，其中现场解吸气体积达解吸气总体积的90%所需时间介于253～521 min，平均约380 min，取心时间介于189～354 min,平均约279 min，页岩气总解吸时间介于549～782 min，平均约659 min，由此计算出t0处于解吸后的131 min左右，对应时间平方根则近似取值为11 min左右。

2.3 基于解吸临界时间点法的页岩含气量计算

对于同一岩心，从任意时间点开始收集数据，最终得到的含气量均应相同。通过确定t0的位置和相应直线斜率，准确计算页岩损失气量，进而获得页岩含气量。

计算过程如图3所示：①对收集到的解吸数据采用多项式函数法进行拟合，因t0后的解吸数据符合非线性关系，因此可将拟合曲线A外推至t0对应的m点；②在m点对多项式函数求导，得到曲线A在该点的切线斜率，根据同一解吸曲线的光滑连续性，该斜率应与初期平衡扩散阶段的解吸曲线斜率相等，依据该斜率反推得到趋势线B并至零时间点；③将曲线AB向上平移，使m点与横坐标轴重合，即为n点，平移后的曲线为CD，由t0前的直线D计算损失气量qD，t0后的累计解吸气量qC可根据曲线A对应的累计解吸气量（qA）和平行上移量（h）计算得到，如式（3）所示，进而由qD、qC即可计算出页岩含气量，如式（4）所示。

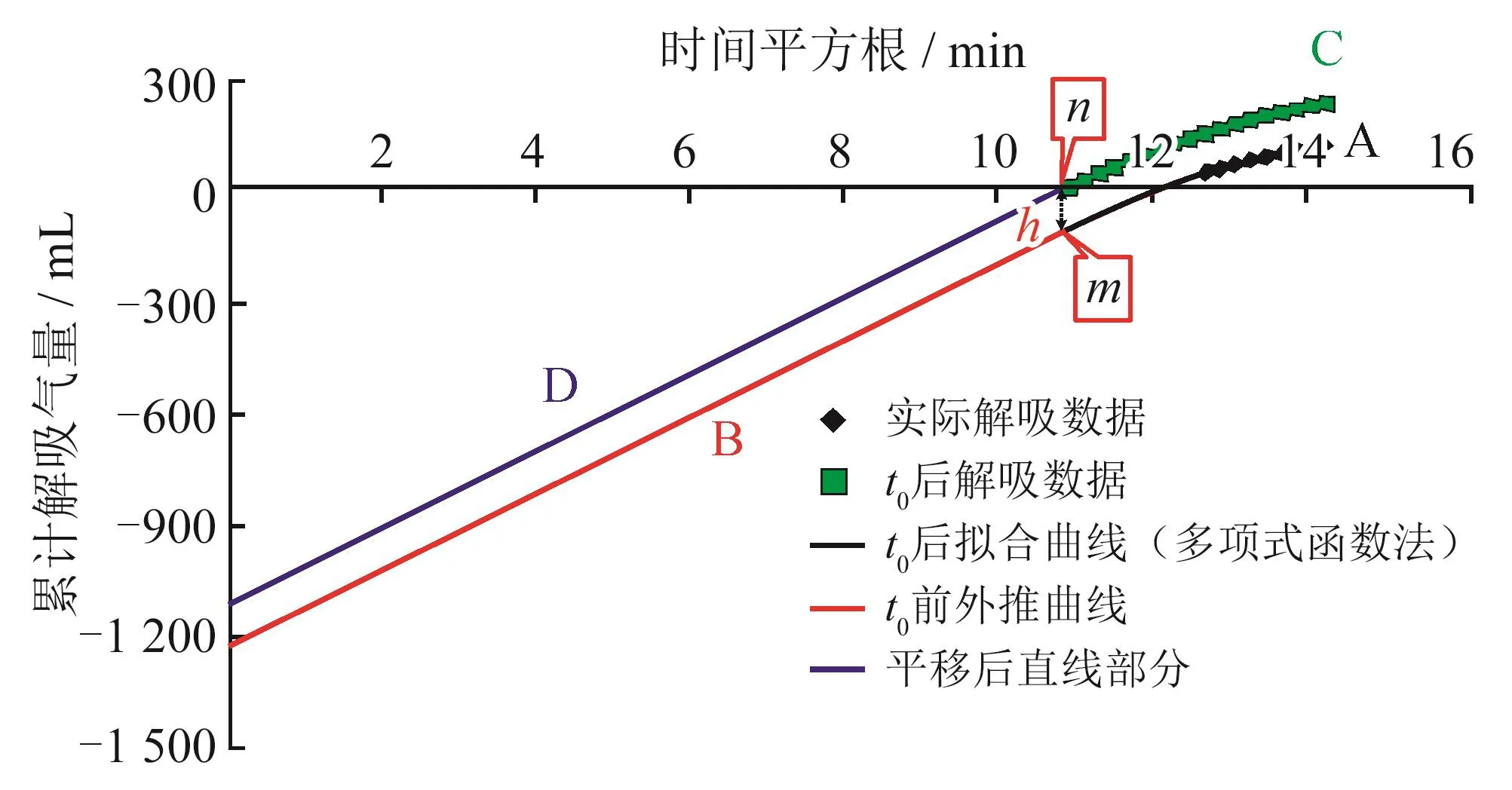
图3 解吸临界时间点法计算过程示意图

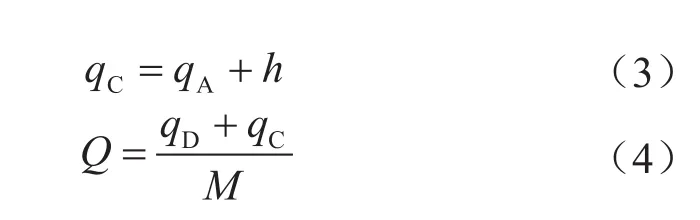
式中qC表示曲线C对应的累计解吸气量，mL；qA表示曲线A对应的累计解吸气量，mL；h表示平行上移量，mL；Q表示页岩含气量，mL /g；qD表示t0时刻对应的损失气量，mL；M表示岩样质量，g。

3 实例应用

目前延长石油集团在鄂尔多斯盆地长7段已完钻多口陆相页岩气井，通过常规取心获取了大量页岩气解吸数据。为准确求取长7段页岩含气量，在同层位的某口页岩气井开展了保压取心工作。选取该井的常规取心岩样，结合取心参数和岩样现场解吸数据（表1），分别采用USBM法、多项式函数法和解吸临界时间点法计算页岩损失气量，进而得到页岩含气量，通过与同层位的保压取心含气量测试结果进行对比来验证解吸临界时间点法的准确性。

表1 常规取心页岩岩样现场解吸数据表

应用USBM法、多项式函数法计算得到的损失气量分别为1 577.35 mL、4 809.00 mL，结合表1中的累计解吸气量和岩石质量计算页岩含气量，通过单位换算后得到相应含气量分别为2.60 m3/t、4.12 m3/t。而应用解吸临界时间点法计算得到损失气量为3448.78 mL，通过平移量（126.61 mL）及现场测得的累计解吸气量（3 986.00 mL）得到解吸临界时间点后累计解吸气量为4 112.61 mL， 最终计算含气量为 3.54 m3/t（图 4）。

图4 三种方法计算页岩损失气量对比图

保压取心岩样含气量测试结果显示含气量（不含残余气量）最高为3.64 m3/t，最低为3.08 m3/t，平均为3.33 m3/t（表2）。基于USBM法和多项式函数法计算的页岩含气量，与保压取心岩样含气量测试结果均存在较大偏差；而采用解吸临界时间点法计算页岩损失气量，得到的页岩含气量与保压取心岩样含气量测试结果较接近。

为进一步验证解吸临界时间点法的准确性，对该井在长7段采用常规取心得到的其他页岩岩样也进行了含气量计算，结果均与保压取心岩样含气量测试结果较接近（表3）。

表2 同层位保压取心页岩岩样含气量测试数据表

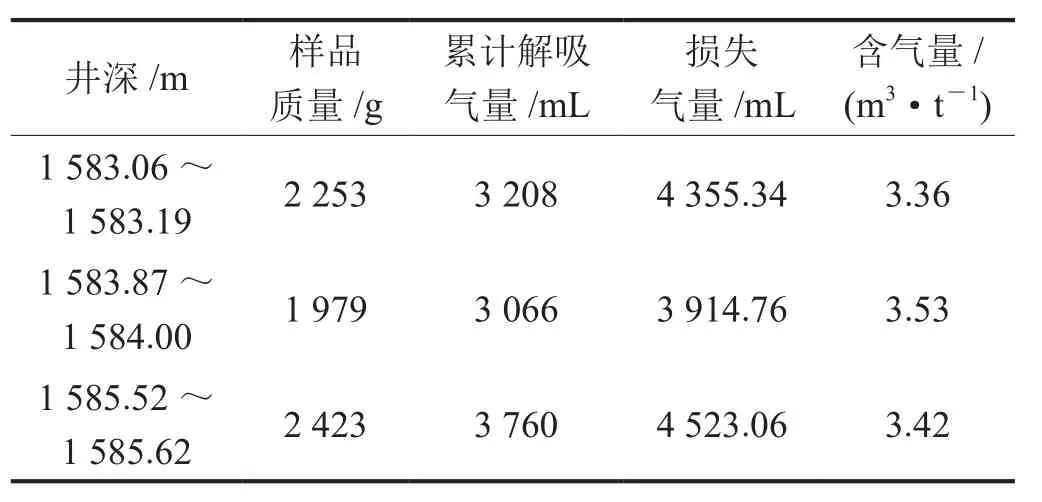
表3 同层位常规取心页岩岩样含气量计算结果表

4 结论

1）解吸临界时间点前的解吸数据符合线性关系且趋势线斜率相同，该时间点后则为后期非平衡扩散阶段，该阶段内不同时间点收集到的解吸数据，均呈非线性关系，且对于同一岩心解吸曲线相互平行。

2）应用USBM法和多项式函数法计算页岩损失气量，进而得到的页岩含气量，含气量计算结果与保压取心岩样含气量测试结果均存在较大偏差；而采用解吸临界时间点法计算得到的含气量与保压取心岩样含气量测试结果较接近，该方法适用性更强。