基于结构方程与蒙特卡洛方法的钻井现场作业风险评价

赵春兰 殷慧敏 王 兵 范翔宇 吴 昊

1.西南石油大学理学院 2.西南石油大学计算机科学学院3.“油气藏地质及开发工程”国家重点实验室·西南石油大学 4.中国石油西南油气田公司勘探事业部

0 引言

油气钻井作业是一个隐蔽性强、有较大的不确定性和高风险的系统工程[1]。随着油气勘探开发的不断发展[2]，钻井作业变得日益频繁，钻井条件和地质条件也越来越复杂，致使钻井作业处于危险的境地，钻井事故也就时有发生[3]。

目前，对于钻井风险的评估方法已有相当多的学者进行研究[4-8]。李环等[4]基于HAZOP定性分析法评估钻井作业风险的大小。李海宏[5]通过层次分析法建立多因素多层次钻井风险定量评价模型，定量分析法因其考虑钻井作业数据来分析问题得以广泛应用。上述都是常规确定性方法，并未考虑评价数据的不确定性，因此，提出了一些不确定性分析方法来解决这些问题。金业权等[6]提出了基于三角模糊数的钻井井控风险定量评价模型；李琪等[3]采用AHP与模糊综合评价相结合的方法建立了钻井风险综合评价模型；以及确定指标权重结合模糊综合评价法评估钻井风险等级的其他方法。因子与指标间的关系存在主观干扰，使得结果出现误差，最终可能导致所确定的权重与实际不符，而常规的权重计算法无法确定各因子之间的直接或间接关系。结构方程模型（SEM）不仅可以很好地解决这个问题[7]，并且可找到关键风险因子。钱志雷等[7]利用SEM构建了石油企业国际石油工程项目的风险评价方法。

但SEM的数据收集困难，其数据往往要求服从正态分布，为了得到更方便的数据样本，基于现场数据各因子的分布特征，借助蒙特卡洛方法（MC）生成一系列服从正态分布的风险因子样本数据。同时由于模糊综合评价法是以专家打分的方式得到评判结果缺乏一定的客观性，而MC是一种利用随机数来解决问题的技术，不但考虑了风险因素变动的幅度，还考虑了这种变动幅度发生的可能性大小及对考察指标的影响程度，使得评价结果更加客观合理。

为了更好地处理数据结构中的不确定性问题，找到关键因子和指标之间的关系，进而得到客观的评价结果，笔者结合上述两种方法建立以危险度（R）来衡量风险程度的SEM—MC新模型，并应用于四川盆地某油气田现场。

1 方法原理

1.1 结构方程模型

SEM是一种基于变量协方差矩阵来分析变量之间关系的多元统计分析方法学[9-11]。它把因子分析与路径分析相结合，对于一些不能直接测量的研究变量用可观测的变量作为潜在变量（以下简称潜变量）的“标志”，利用因子分析的方法将观测变量与潜变量联系起来，结合路径分析找到潜变量之间的结构关系[12]。

SEM分为测量模型和结构模型两部分，如图1所示。

测量模型主要用来描述外源（内生）观测变量与外源（内生）潜变量之间的关系，由两个典型的因子模型组成，即

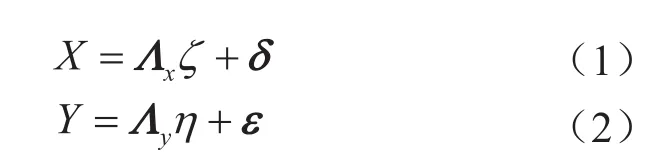
结构模型主要是描述潜变量之间的关系，包括外源潜变量对内生潜变量的影响，以及内生潜变量之间的影响，是一种因果模型[12-13]，即

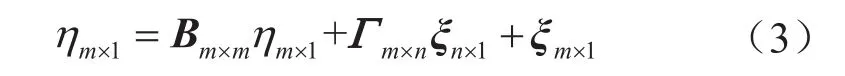
式中δ表示外源观测变量X的测量误差向量；ε表示内生观测变量Y的测量误差向量；Λx表示外源观测变量关于外源潜变量的负载矩阵；Λy表示内生观测变量关于内生潜变量的负载矩阵；Гm×n表示外源潜变量对内生潜变量的影响系数矩阵；Bm×m表示内生潜变量之间的影响系数矩阵；ξ表示结构误差向量[9,12-13]。

式（1）规定了外源潜变量（ζ）和外源观测变量（X）之间的联系，式（2）规定了内生潜变量（η）和内生观测变量（Y）之间的关系，式（3）规定了外源潜变量与内生潜变量、内生潜变量与自身之间的关系。

1.2 蒙特卡洛方法

MC属于试验数学的一个分支，它利用随机数进行统计试验，能够随机模拟各变量间的动态关系[14]，得到大量模拟测量结果并分析，进而解决某些复杂的不确定性或风险性问题。

笔者基本研究思路如下：

假设随机变量X的数学期望E（X）是需要计算的变量，X1, X2, …, XN是一系列随机数重复采样N次得到的。本系列的平均值计算如下[15]：

根据大数定律，当N的采样次数足够多时，即为

通过使用MC方法来评估钻井风险等级，可以根据每个变量的分布生成一系列样本数据，确定事故后果与风险因素之间的关系。

对于多维随机变量的MC模拟问题，往往假定各随机变量是相互独立的，而在某些实际应用中，多维随机变量却具有一定的相关性。一般多维相关正态分布随机变量序列可以通过协方差矩阵的Cholesky因子对独立正态分布随机变量序列进行线性变换来产生[16]。基于研究目的，笔者运用SEM中得到的变量间的线性模型来求得事故后果与各风险因素关系进行MC模拟，并利用@Risk7.5软件来执行。

1.3 SEM—MC新评估模型的构建

对于相同的危险度数值，一般模型只考虑了其事故后果分值与事故可能性指标分值的简单累积，这不能真实反映客观风险水平[17]。为此，笔者提出了SEM—MC的钻井风险新评估模型。

针对钻井现场作业风险因素具有的不确定性，首先构建钻井现场作业风险因子，利用SEM求出各风险因子的相关性，并求得指标权重确定关键风险因子，再由各因子的数据分布特征，利用MC进行模拟，求得潜变量的模拟值，结合事故后果值及其指标权重建立SEM—MC的钻井风险新评估模型（图2）。

其构思的3个步骤：①通过收集钻井风险数据，删除不显著因子，确定风险指标体系；②结合SEM求得风险因子权重，以识别影响钻井现场作业安全的关键风险因子，同时利用风险后果权重以确定事故后果的程度；③根据风险因子的数据特征结合步骤2的测量模型，利用MC模拟出潜变量的模拟值（即事故可能性因素分值）；④最后利用MC模拟事故可能性因素分值与事故后果严重程度累积的风险评估新模型，即

式中R表示危险度；PXi表示事故可能性因素分值，ωi表示事故后果影响权重；Y1i表示事故后果分值；ωiY1i表示事故后果程度。

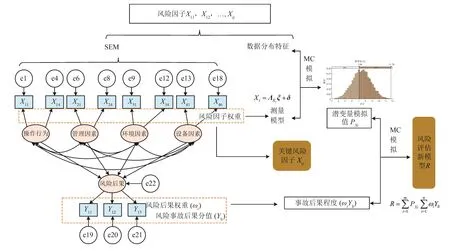
图2 SEM—MC风险评估新模型构思图

2 钻井作业风险评价指标的确定

2.1 数据收集

油气钻井作业的风险指标体系具有复杂性、多层次的特点[7]，其现场作业风险因素较多，通过收集现场数据、咨询钻井作业专家并结合因子分析[18]，确定操作行为、管理因素等4个方面的因素，违章作业、生产管理缺陷等18个钻井作业风险指标以及涉及人员、设备事故[19-21]和环境污染这3种事故后果。对四川盆地某油气田钻井现场数据进行收集，主要收集2011年365 天内各风险指标每天发生的次数以及所造成事故的情况。各指标部分数据如表1所示。

2.2 数据处理

2.2.1 异常值处理

异常值是指样本中的个别数值明显偏离其所属样本的其他观测值，因其会对结果造成一定的影响。笔者利用iForest算法对数据进行异常值处理，寻找出与大部分数据不一样的异常数据，将其中与研究规律不符合，干扰结果的数据从中剔除，最后共剔除包含日期（月/日）为3/23、3/26、4/5、4/12等19个异常样本值。

2.2.2 数据的正态性检验

考虑到结构方程模型一般是问卷调查获得的数据，且要求数据服从正态分布。基于本文所用的是真实观测数据，无法直接进行AMOS分析。因此需要先进行正态性检验和等级变换分析。

通过累积频率来了解各个指标值的分布情况，首先利用Matlab软件计算2011年各个指标的频率，先将数据通过快速排序方法进行排序，再按数组下标进行扫描，记录频数，最后计算得到如场所不符合要求（图3-a）和井控设备缺陷（图3-b）等指标的累积频率。

2.2.3 等级程度的划分

利用正态分布数据的特性，根据风险因子每天发生次数的频率划分等级，发生次数越少导致事故发生的可能性越小，反之越大。按正态分布函数，以置信区间概率 [0 20%）、[20% 40%）、[40% 60%）、[60%80%）、[80% 100%） 作为风险等级划分的基本区间，分别记为安全，较安全，一般，较危险，很危险等5个等级程度，且按照1～5分进行打分，将每个风险因子导致事故的可能性分值记为PXij（Xij表示风险因子）。按照上述方法对风险指标进行处理，以作业场所不符合和井控设备缺陷为例（图4），最后各风险指标导致事故的可能性分值部分数据如表2所示。

从图4可以看出，井控设备缺陷的累积频率在 0处接近10%，在10以上不到10%，由此说明大部分值处于（0, 10）。因正态分布与伽马分布均具有这样的特征，即图3中指标与正态分布和伽马分布的累积频率图像类似，所以钻井风险的各指标值大致服从正态分布。

表1 四川盆地某油气田钻井现场作业2011年各风险指标及事故后果发生次数表

3 实例分析

3.1 模型的构建

3.1.1 钻井现场作业风险结构方程模型的设定

根据钻井现场作业风险的理论知识与相关经验，操作行为、管理因素、环境因素和设备因素直接影响到钻井作业的安全问题，同时这些因素之间也存在着一定的内在联系，基于此构建如图5所示的结构方程模型。

图3 部分指标的频率累积图

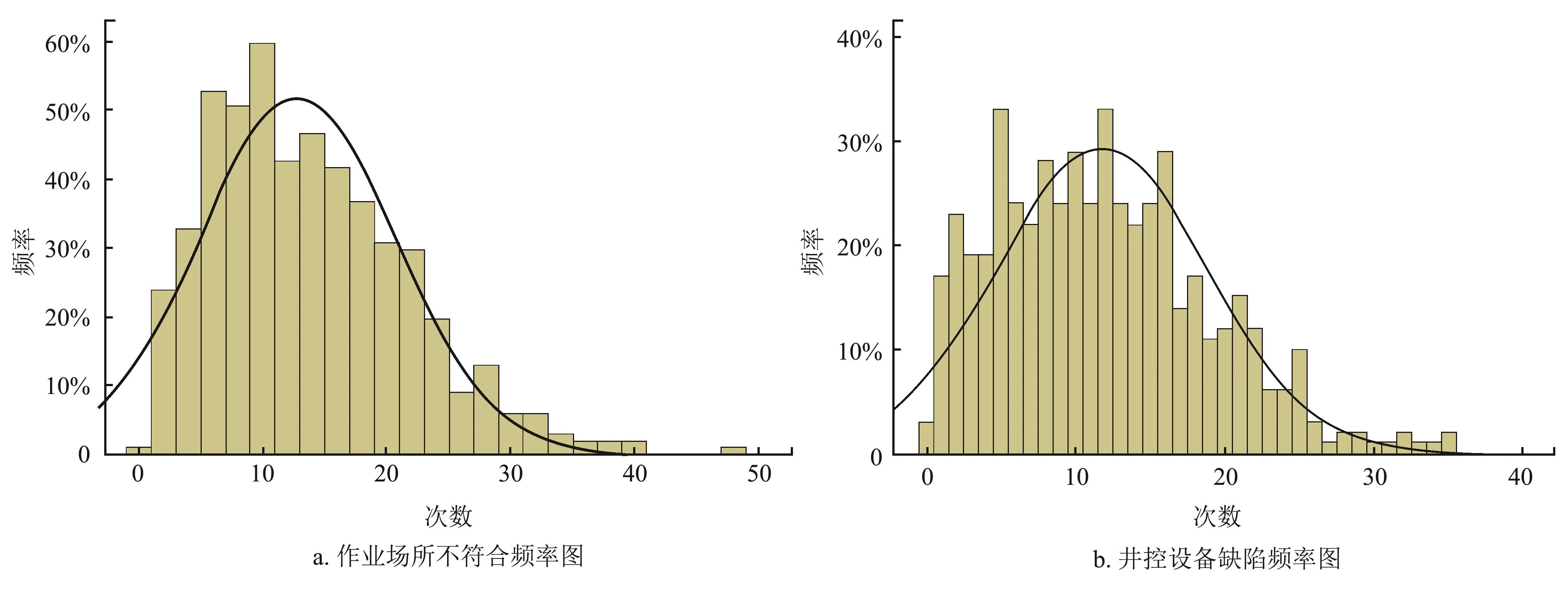
图4 部分指标的正态分布频率图

表2 四川盆地某油气田钻井现场作业2011年各指标导致事故的可能性及事故后果分值部分数据表

利用SPSS 20.0对处理后的数据进行因子分析，提取公因子并设定其为潜变量，分为作业人员的操作行为X1、管理层的管理因素X2以及环境因素X3、设备因素X4和钻井风险Y，其下对应为各自的观测变量，所以确立测量模型及结构模型如图5所示。

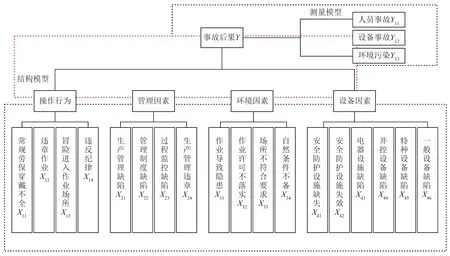
图5 钻井风险结构方程模型

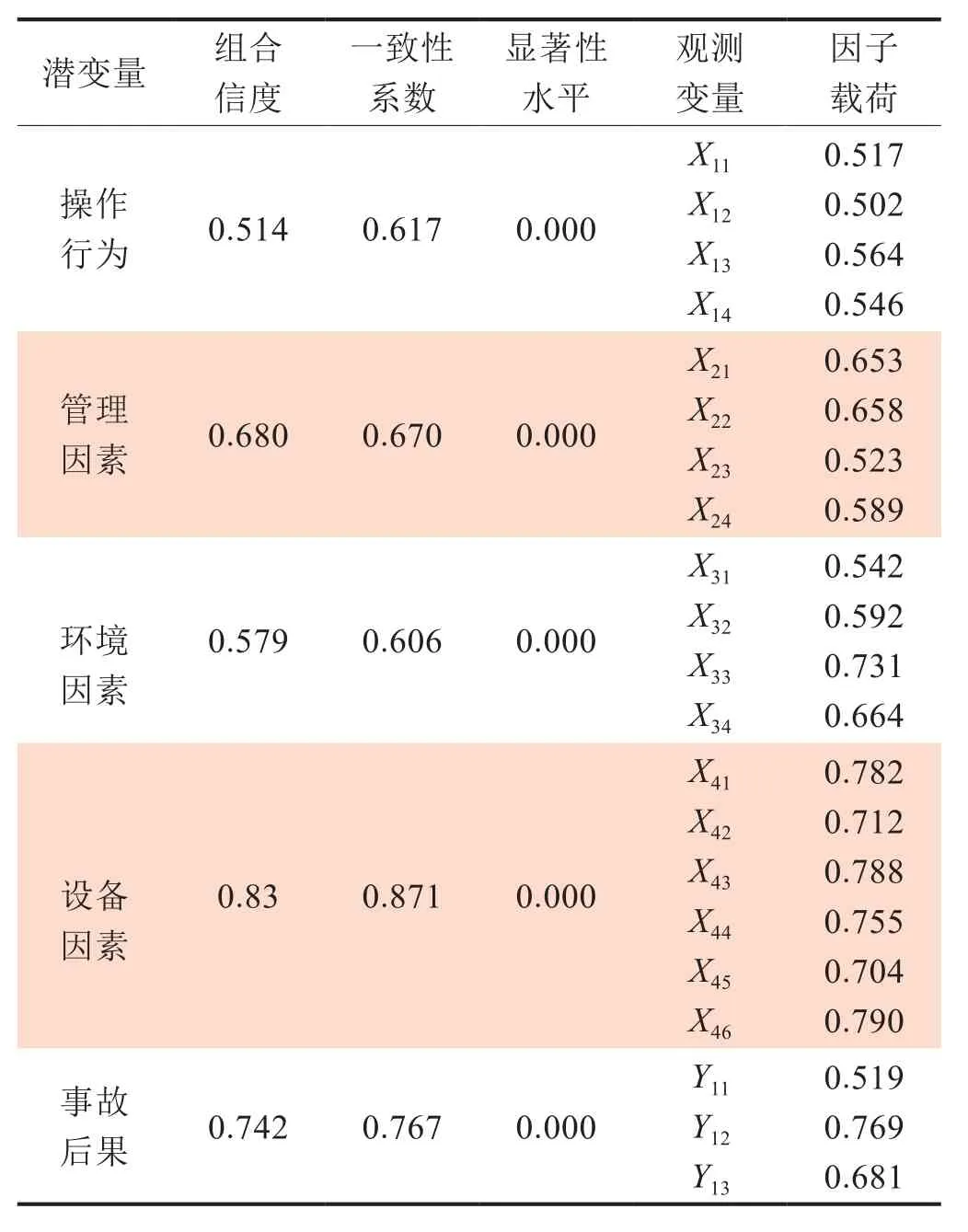
表3 信度与效度检验表

3.1.2 模型检验

测量模型主要根据可信度和效度进行判定，可信度的参数由潜变量的组合信度和一致性系数组成[22]，运用SPSS 20.0进行因子分析计算的结果如表3所示。由表3可知，所有潜变量的组合信度和一致性系数都大于0.5，显著性检验指标为0.000明显小于显著性水平，表明了测量模型具有较好的可信度。同时，各观测变量的因子载荷都接近0.5，说明潜变量的结构效度较好。

3.1.3 模型的拟合及评价

通过对模型进行反复的修正和拟合，依据AMOS软件输出的拟合指数进行判断，建立的SEM的各项适配度指标检验结果如表4所示。检验结果显示，模型的多项拟合指数均符合要求，拟合效果较好，模型是合理的，且修正后的模型比原模型拟合优度更高，故采纳修正后的模型[23]。

将处理后的数据导入AMOS软件中，得到标准化估计结果，如表5和图6所示。

3.1.4 模型分析

由图6和表5可知[23]，根据SEM结构模型得到可观测潜变量因素之间关系，潜变量如操作行为、管理因素、环境因素、设备因素分别与钻井事故后果的相关系数依次为0.32、0.50、0.31、0.42；而管理因素与设备因素的关系为0.93，与环境因素的关系为0.92，设备因素和环境因素关系为0.94。由此可见，管理因素对事故后果影响最大，其次是设备因素，环境因素影响最小。同样，根据测量模型可得各风险因子间关系，风险因子如作业场所不符合与一般设备缺陷的关系0.57为最大，其次是场所不符合与安全防范设施缺失，电器设施缺陷关系为0.56，违章作业和管理制度缺陷关系0.06为最小。

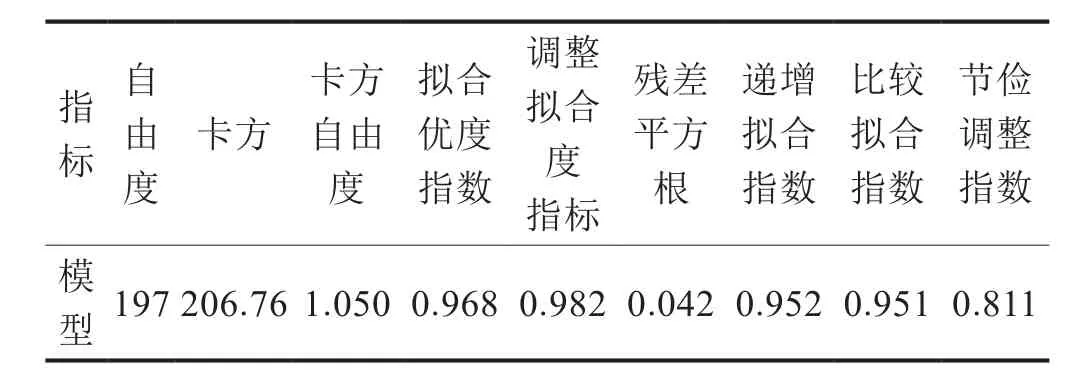
表4 SEM模型拟合效果检验表

表5 部分参数估计及其检验表

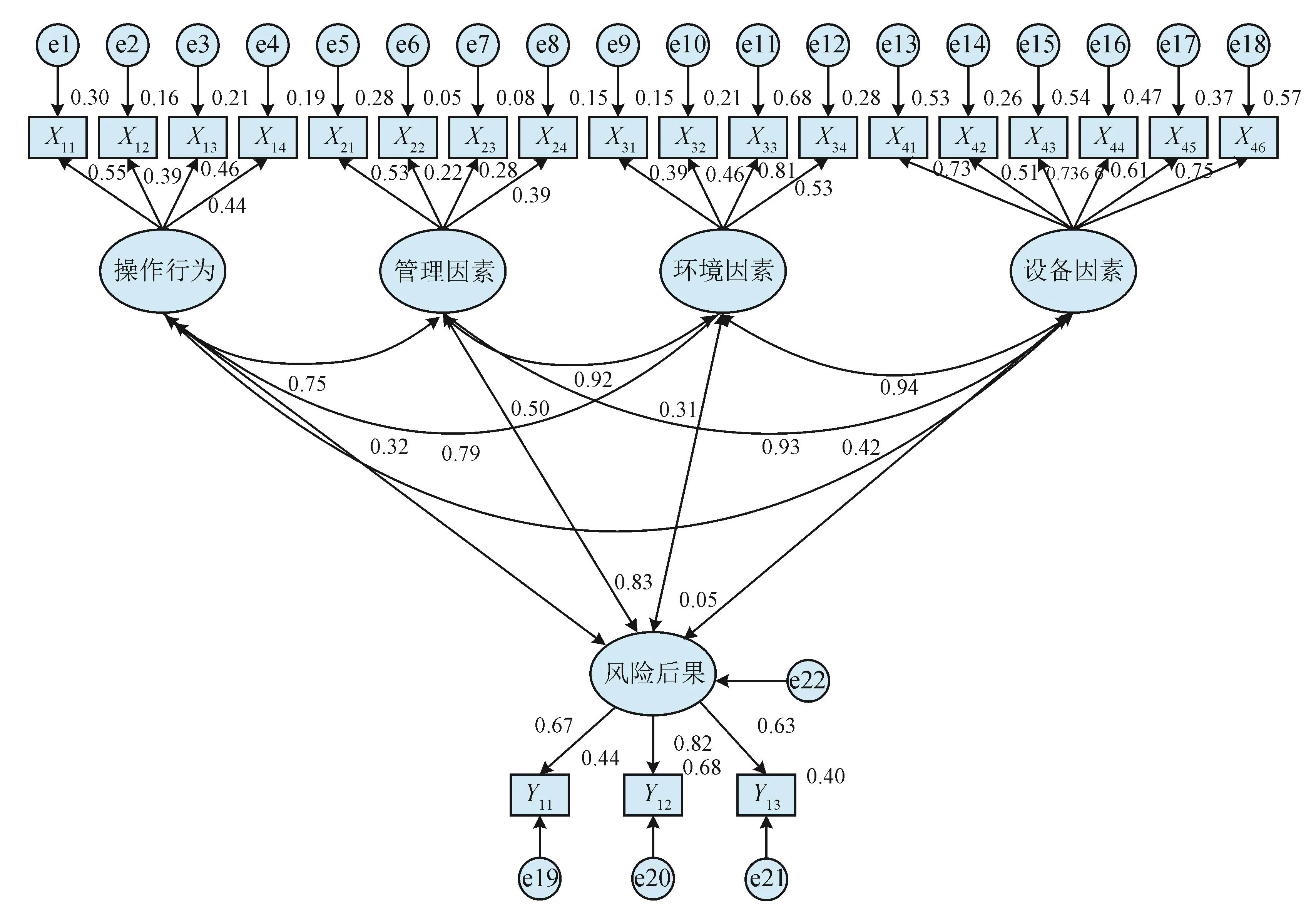
图6 钻井现场作业风险模型标准化估计结果图

根据路径分析求得各风险因子的标准化系数作为权重大小，找到关键因子。潜变量在操作行为中的关键风险因子为常规劳保穿戴不齐（X13），管理因素的关键风险因子是生产管理缺陷（X21），环境因素中是作业场所不符合（X33），设备因素中是一般设备缺陷（X46）。

在结构方程模型中，由于内生潜变量事故后果受操作行为等4个外源潜变量的影响，以及人员事故等3个观测潜变量的共同作用，且通过观测潜变量来表现。

由式（1）～（3），可得

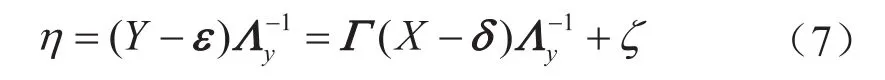
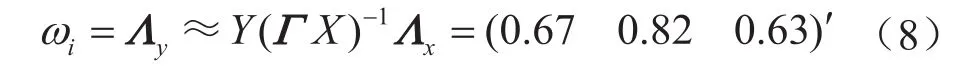
3.2 建立SEM—MC的钻井现场作业风险评价

3.2.1 风险等级的确定[24]

由前面对本文数据的分析可知，基于结构方程模型的正态性检验，确定各风险因子的分布范围及其峰值。利用MC随机模拟程序对给定的各个因素区间内随机地获取5 000个数值[14]，根据表3确定的风险因子导致事故的可能性分值（PXij），通过SEM测量模型式（1）可以确定PXi（即外源潜变量的可能性分值），基于MC中对各风险因子的模拟数可得潜变量的模拟值变动范围以及变动范围发生的可能性大小，如表6和图7所示（以潜变量X1为例）。

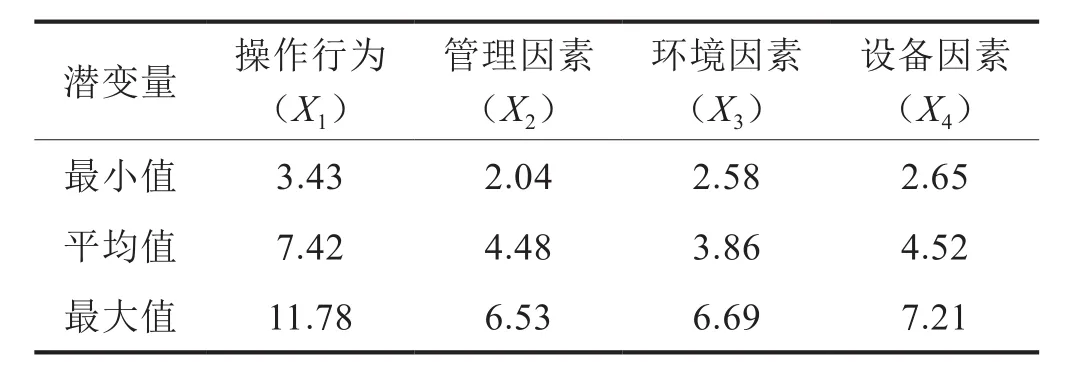
表6 潜变量的模拟值表

图7 潜变量X1的模拟值随机概率分布图

由表6所示，结合事故后果程度得到风险评估新模型，最后生成该钻井现场作业危险度的随机概率分布和累积概率图如图8所示。由此可以知道钻井风险的可能性结果以及每个结果出现的可能性，还可以得到一定置信水平下的现场作业风险范围。根据正态分布函数，以风险置信区间[0 20%）、[20%40%）、[40% 60%）、[60% 100%）、[80% 100%）来划分风险等级[17]，由正态分布函数数值表，可确定各风险等级的阈值区间于表7中。当置信度取40%时，计算得到的风险值范围为[95 101]，故此范围内的风险值是属于安全范围的。

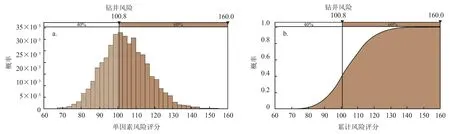
图8 危险度随机概率分布图和累积概率图

表7 SEM—MC的风险等级阈值表

利用MC模拟进行5 000次迭代计算后，得到模拟结果R = 108.9，结合表7，可知该钻井现场作业风险处于一般等级，与实际情况相符。

3.2.2 与其他方法的对比

通过风险因子导致事故的可能性分值与事故后果指标分值的累积[17]，可以对钻井现场作业进行评判，建立危险度模型由此确定的风险等级如表8所示。该钻井现场作业的风险等级阈值与SEM—MC的方法存在不同，其风险等级阈值范围比风险评估新模型更大，这可能是由于SEM—MC方法考虑了各风险因子之间的关系，使得彼此之间的可能性分值不存在叠加效应，避免了重复信息。此外，基于SEM的测量模型，MC模拟出潜变量的可能性分值，并结合危险度确定风险等级，使得评估结果更符合实际情况。

表8 R*[17]与SEM—MC风险等级阈值比较表

4 结论与建议

笔者首次提出了结构方程模型和蒙特卡洛模拟相结合的钻井现场作业风险评价新方法，其评价结果可对钻井作业现场作业安全风险管理具有重要参考作用。

1）通过结构方程模型确定了钻井现场作业风险体系的指标权重，克服了无法确定各因子间的相关性以及权重的主观性，此结构模型结合蒙特卡洛模拟求得危险度用以衡量风险等级，为钻井现场作业风险评价提供一种新的评价方法。

2）根据结构模型可知，操作行为和环境因素对钻井风险影响较小，而整个钻井作业风险体系中管理因素占有最大的比例，说明管理层人员应该加强标准安全管理知识，要有超前的风险意识，让操作人员有更好的保障，才能有效地减少人员安全事故的发生。

3）利用测量模型求得各风险因子的权重大小并找到关键风险因子。场所不符合要求和一般设备缺陷是两个主要关键因子，其相关系数为0.57。操作行为的关键因子是常规劳保穿戴不齐，其与场所不符合要求的相关系数为0.35。说明对于员工在施工前进行安全教育是很有必要的，可以增强员工的安全意识。同时管理人员应注重与施工人员的沟通，对注意事项进行重点讲解，防止不规范不安全行为发生。

4）基于蒙特卡洛模拟钻井风险因子，根据每个风险变量的分布特征生成一系列符合要求的样本数据，最终得到钻井风险值的概率分布，使得评价结果更加贴切于实际情况。