基于Stackelberg模型的PPP项目股权结构研究

何亚伯，李 璨，张 浩

(武汉大学 土木建筑工程学院，湖北 武汉 430072)

近年来，政府和社会资本合作(public private partnership，PPP)成为建筑工程项目中常见的投资模式，结合了政府部门的社会责任、远景规划、协调能力与社会资本的创业精神、社会资金和管理效率，具有建设效率高、充分发挥资金价值及合作双方优势等特点。自2014年以来，政府出台了一系列的相关政策，有效地提升了PPP项目市场信心。2018年10月，国务院办公厅相继发布的《关于聚焦企业关切进一步推动优化营商环境政策落实的通知》和《关于保持基础设施领域补短板力度的指导意见》，进一步明确提出要规范有序地推进政府和社会资本合作项目。

PPP项目实务中，由于政府方和社会资本方资金来源性质不同，项目目标存在差异，致使双方在开展PPP项目合作时产生冲突。一方面，政府方与社会资本方均希望以较少的资金发起项目，利用有限的资金撬动更多的建设项目，改善自身的财务指标。对项目本身来说，股比越低，意味着净现值、内部收益率和投资回收期等投资指标越高。另一方面，较高的自有资金投入可能会导致社会资本方积极性和努力程度下降，带来一定程度的项目质量、进度和造价风险。因此，双方在项目前期和招投标阶段围绕股权结构展开博弈，以期得到最优的股比分配和资本金出资方案。

目前PPP研究着重于项目的风险识别和分配、绩效评价及特许经营期、可行性缺口补贴等指标的博弈，而对于项目公司股权结构的博弈以及相应激励机制的研究较少。政府方与社会资本方的股权分配不仅是PPP项目实际操作中双方关注的焦点问题，还具有非常重要的学术价值。

因此，笔者综合考虑PPP项目中政府方与社会资本方的利益，建立合理的股权结构与激励机制，发挥双方优势，推动项目进程，对PPP项目平稳运营具有非常重要的意义。

1 文献综述

对于PPP项目股权结构选择与激励机制的研究，近几年才逐渐得到相关学者的关注。通过文献进行梳理分析和归纳总结，笔者将相关研究分为以下几类：

(1)影响PPP项目股权结构因素的实证研究。刘婷等[1]通过分析18个典型项目案例，考虑其股权结构和债本比例，归纳不同类型PPP项目的资产特征与能力需求。李艳秋[2]对项目股权结构进行合理划分，识别其类型选择的影响因子。张博[3]从我国PPP项目的现状数据着手，分析项目融资特点，总结影响股本投资规模的关键因素。盛和太[4]通过大量的文献与案例分析，对PPP项目资本结构进行梳理总结。

(2)关于PPP项目最优股权结构的实证研究。阮璐洁[5]分析不同项目公司股权结构下的各方收益，找到最佳股权结构。STAMBROOK[6]通过案例研究，提出了“谁最终承受PPP项目的失败或破产”的问题，对政府如何预防失败、破产提出了建议措施。盛和太等[7-8]结合养老项目、高速公路项目，探讨项目股权结构或最优股权分配问题，以降低风险，增加收益。

(3)建立优化模型，通过分析求解得到最优的股权比例。江春霞等[9]从成本角度建立模型，分析社会资本方的股权比例范围和准入门槛。沈俊鑫等[10]运用Markowitz模型，为政府方和社会资本方对PPP项目不同实施阶段的股权结构调整提供决策参考。郝书君等[11]基于Shapley值利益分配模型，计算各方利益分配。冯珂等[12]基于债权人、私人部门和公共部门三方约束建立模型，为项目股权配置提供决策支持。杨文安等[13]结合轨道交通项目建模，提供可行的决策思路和新的研究视角。吕雁琴等[14]建立博弈模型，探讨政企合作双方在完全与非完全信息状态下的博弈情况。BAKATJAN等[15]基于多财务指标的资本结构选择，从发起人(权益投资者)角度建立线性规划优化模型。MOSZORO[16]基于政府方成本优势的假设，建立资本结构模型，推导最优的私人持股比例。

目前关于公司融资和公司资本结构选择方面，已取得了十分成熟的研究成果，方法理论也较为成熟。而PPP项目的项目公司，作为特殊目的的实体(special purpose vehicle, SPV)，其融资方式和资本结构选择具有特殊性，相关研究也起步较晚，故仍具有广阔的研究空间。

从PPP项目实务角度来看，政府方更多的是从成本和资本金的角度进行投资决策，利用博弈中的优势地位，确定对己方最有利的股权结构，而对于项目的安全、质量与社会资本方激励的考虑有所欠缺。

因此，笔者从政府方角度考虑股权结构对于社会资本方的激励作用，并结合委托代理理论与实际运营问题，对经营性PPP项目中的股权结构进行研究，丰富PPP项目股权结构的相关研究内容。

2 模型构建

PPP项目公司社会资本方来源大致分为两类，一类是建设商、设备供应商、运营商、国际贸易公司等专业公司，另一类是金融机构等纯投资者。假设PPP项目公司社会资本方为建设商形成的联合体，政府方为地方政府下属的某投资公司，双方就PPP项目公司股权比例进行博弈。

2.1 模型背景

PPP项目往往涉及到大型基础设施建设，例如高速公路、综合管廊等，都需要投入大量的资金。政府方与社会资本方共同出资成立项目公司，负责项目的融资、招标采购、建设与运营工作。社会资本方具有多重身份：作为投资商和项目公司股东在工程建设前期投入项目资本金，作为总承包商和建设商负责工程的设计、采购、分包、施工等工作，作为运营商对竣工后的项目进行运营和维护。

项目可分为建设阶段(项目合同签订、工程建造基本完成)与运营阶段。建设阶段是指从立项到施工建造、设备安装基本完成的阶段。项目的融资方式为：政府方发起项目，基于委托代理理论引入社会资本方作为另一股东，共同建立项目公司，投入资金占项目总投资额的比例为γ，其余资金来源于银行等金融机构贷款。

2.2 Stackelberg模型

Stackelberg博弈，属于完全信息动态博弈模型，其博弈过程为：①第一期，上级决策者(leader)确定并宣布己方的决策；②第二期，下级决策者(follower)观测到上级决策者的决策后，根据己方的最优反应，做出相应的决策；③博弈结束，双方的收益确定。

博弈双方均了解对方的收益函数，因此上级决策者能够预先得知下级决策者的最优反应，从而将其考虑到自身的决策中。

笔者基于政府角度分析，考虑对于社会资本方的激励作用，假设政府方的决策变量为PPP项目公司股权结构，社会资本方决策变量为努力程度。博弈过程如下：①第一期，政府方确定并宣布PPP项目公司的股权结构。②第二期，社会资本方接受该股权结构，双方共同出资成立项目公司。社会资本方作为建设商，根据其接受的股权结构，选择己方在项目实施过程中的努力程度。由于政府方了解社会资本方在不同股权结构下，将选择对己方最有利的努力程度，因此会在决策阶段考虑到股权比例对社会资本方的激励作用。③博弈结束，双方的收益确定。

2.3 模型建立

根据以上讨论，笔者建立了Stackelberg动态博弈模型，用以刻画政府方和社会资本方关于股权结构的博弈过程。模型参数如表1所示。

表1 模型参数

令项目建设阶段的工期为Tt，其表达式为：

Tt=Tf-ηα

(1)

由上述公式模型可以看出，社会资本方在建设中越努力，努力程度越大，工期随之缩短，符合实际情况。

假设工程建造成本为Ct，建造成本包含可变成本Cv与固定成本Cf，即：

Ct=Cf+Cv

(2)

其中,固定成本Cf为定值，可通过前期测算得出。根据文献[7]，将可变成本Cv表示为：

(3)

在实际项目中，项目合同签订时就已经确定了特许经营期的时间Tm，假设Tm为定值。考虑资金占用成本，为方便模型构建，假设资金为项目建造初期一次性从金融机构贷出投入项目，并采用单利计息方式计算其在建设期与经营期的资金占用成本。为简化模型，资金占用成本Co以单利计息方式计算：

Co=R(1-γ)(Tm+Tt)i

(4)

式中：R(1-γ)为项目资本金借贷金额；Tm+Tt为项目全周期年限；i为利率。

项目公司的收益NI为特许经营期的经营收益与资金投入、资金占用成本差值。假设项目特许经营期单位年限平均利润为r，且r与努力程度系数相关，则有：

r=π+αf

(5)

存在一个基准利润π，且社会资本方努力程度越大时，实际平均利润r越大，符合实际情况。也可以结合实际情况理解为，社会资本方努力程度越大，工程质量水平提高，特许经营期内运营维护费降低，则实际利润越大。

项目公司期望收益函数的表达式为：

NI=Tm(π+αf)-R(1-γ)-Co

(6)

在项目建设运营过程中，社会资本方既是股东(委托方)，又是代理方，具有双层角色。因此，其收益由项目分红与建设施工利润共同构成。社会资本方收入项为建造期的施工利润(即建造期收益)与项目公司分红(即经营期收益)之和。支出项为项目资金投入金额。即社会资本方期望收益函数可表示为：

NISC=Rθ-Ct+kNI-Rkγ

(7)

政府方收益为经营期分红收益与项目资金投入金额差值，其收益函数可表示为：

NISG=(1-k)NI-Rγ(1-k)

(8)

综上，整理得到以下Stackelberg博弈模型：

(9)

(10)

3 模型求解

通常采用逆向归纳法对Stackelberg模型进行求解：首先，对社会资本方的收益函数进行优化，得到给定股比k下社会资本方的最优努力程度α*。其中，社会资本方根据政府方给定的股比做出反应，选择最优努力程度，因此最优努力程度是股比的函数，称为最优反应函数，记为α*(k)。其次，将该最优反应函数代入到政府方的收益函数中，通过优化求解最优股权比例k*。最后，将最优股权比例代入至最优反应函数中，计算得到社会资本方的最优努力程度α*(k*)。

证明将式(6)代入式(7)可得：

NISC=Rθ-Ct+kTm(π+αf)-

kR(1-γ)-kCo-Rkγ

对决策变量求导，使导数等于零，得出此种情境下的最优反应函数：

(11)

社会资本方达到最优努力程度时，有建设期最佳工期时间，对决策变量求二次导数的结果为-λ，恒小于零，故可得出存在唯一最优努力程度使得社会资本方收益取得最大值。

定理1博弈模型的子博弈纳什均衡解为：

证明根据引理1，社会资本方和项目公司的最优收益分别为：

kR(1-γ)[1+(Tm+Tf-

(12)

R(1-γ)[1+(Tm+Tf-

(13)

政府方收益为经营期分红收益与项目资金投入金额差值。故政府方的期望收益函数为：

NISG=(1-k)Tm(π+

(1-k)R(1-γ)[1+(Tm+

RSCγ(1-k)

(14)

由模型可知，R(γ-1)[1+(Tm+Tf)i]为财务成本负值，Tmπ为特许经营期基准利润。从经验角度分析，特许经营期基准利润必然可以覆盖财务成本，故有R(γ-1)[1+(Tm+Tf)i]+Tmπ>0。则政府方的期望收益函数为：

NISG=(1-k)(M+Nk)-Rγ(1-k)

对k求导可得最优股比为：

(15)

将其代入到最优反应函数中可得：

(16)

4 模型分析

4.1 参数变动对于政府方最优股比的影响

Rγ+R(1-γ)[1+(Tm+Tf)i]-

(17)

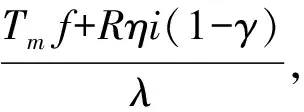
因此，当项目特许经营期较长或利润波动明显时，为达到政府收益最大化，政府方作为发起人，应掌握控股权。反之，当项目特许经营期较短或利润受努力程度影响不大时，社会资本方应掌握控股权。

(2)参数变化对最优股比影响。①项目资本金比例对股比的影响如图1所示，可以看出项目资本金的比例越高，社会资本方占比越高；随着特许经营期的延长，项目资本金变化对最优股比的影响程度减弱。②可变成本对努力系数敏感性对最优股比的影响如图2所示，可以看出可变成本对努力系数敏感性越高，社会资本方占比越高；随着特许经营期的延长，可变成本对努力系数敏感性变化对最优股比的影响程度减弱。③工期受努力系数反应程度对股比的影响如图3所示，可以看出工期受努力系数反应程度越强，社会资本方占比越低；随着特许经营期的延长，可变成本对努力系数敏感性变化对最优股比的影响程度减弱。

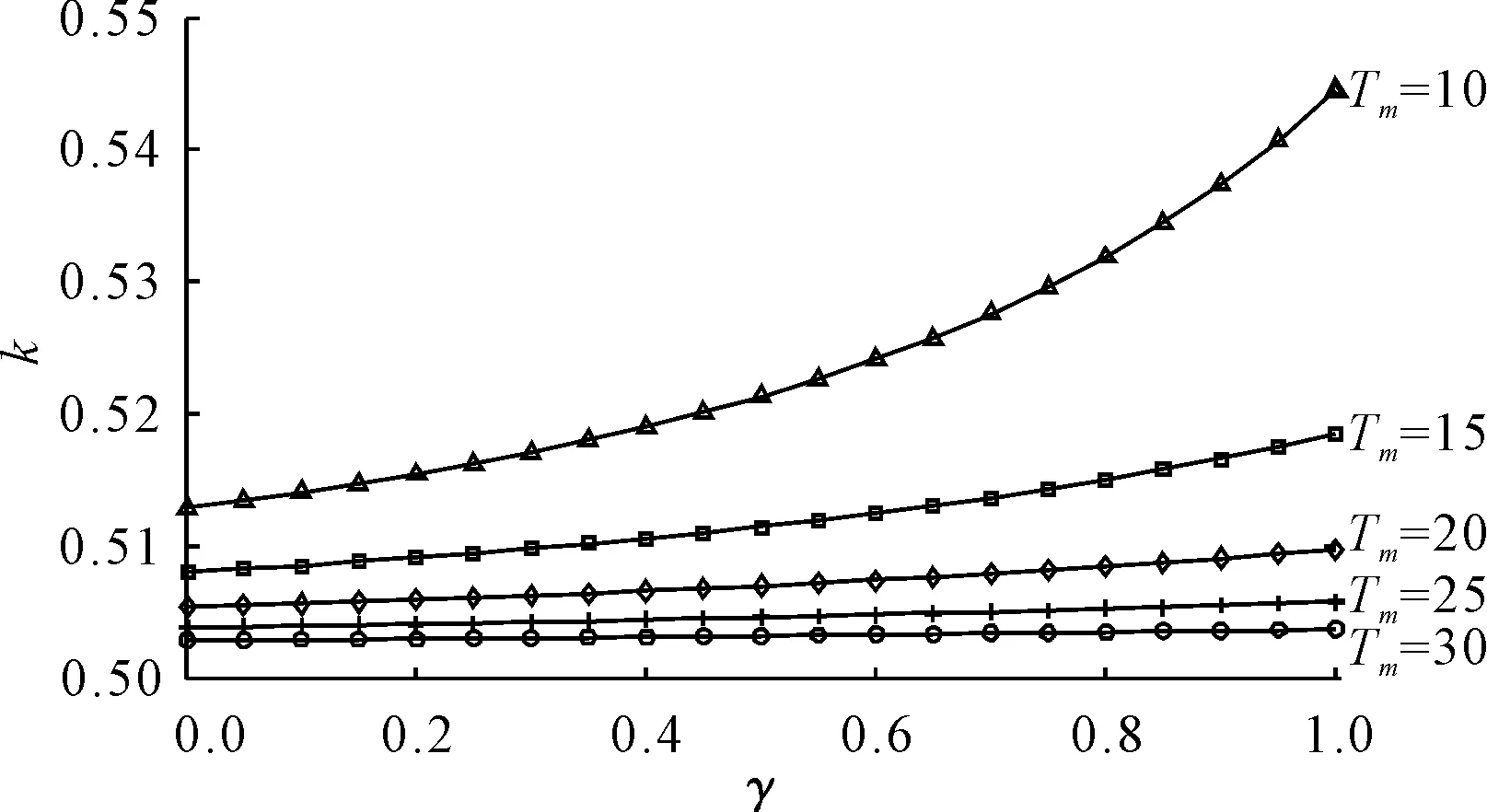
图1 项目资本金比例γ对股比k的影响

图2 可变成本对努力系数敏感性λ对股比k的影响

图3 工期受努力系数反应程度η对股比k的影响

通过以上参数变化对于最优股比的影响，可得出如下推论。

推论1最优股比k与项目资本金γ、可变成本对努力系数敏感性λ呈正相关关系。当γ、λ增大时，k随之增大；当γ、λ减小时，k随之减小。

推论2最优股比k与工期受努力系数反应程度η呈负相关关系。当η增大时，k反而减小；当η减小时，k反而减小。

推论3最优股比k与特许经营期Tm呈负相关关系。当Tm增大时，k反而减小；当Tm减小时，k反而增大。

4.2 参数变动对于社会资本方最优努力程度的影响

①项目资本金比例对最优努力程度的影响如图4所示，可以看出最优努力与项目资本金比例呈负相关关系，随着项目资本金比例的升高，最优努力程度有所下降。随着特许经营期的延长，最优努力系数会有所提升。②可变成本对努力系数敏感性对最优努力程度的影响如图5所示，可以看出随着可变成本对努力系数敏感性的提升，最优努力程度有所下降。随着特许经营期的延长，最优努力系数会有所提升。③工期受努力系数反应程度对最优努力程度的影响如图6所示，可以看出最优努力与工期受努力系数反应程度呈正相关关系，随着工期受努力系数反应程度的增强，最优努力程度有所下降。随着特许经营期的延长，最优努力系数会有所提升。④工期对可变成本反应程度对最优努力程度的影响如图7所示，可以看出最优努力受工期对可变成本反应程度的影响不大。而随着特许经营期的延长，最优努力系数会有所提升。

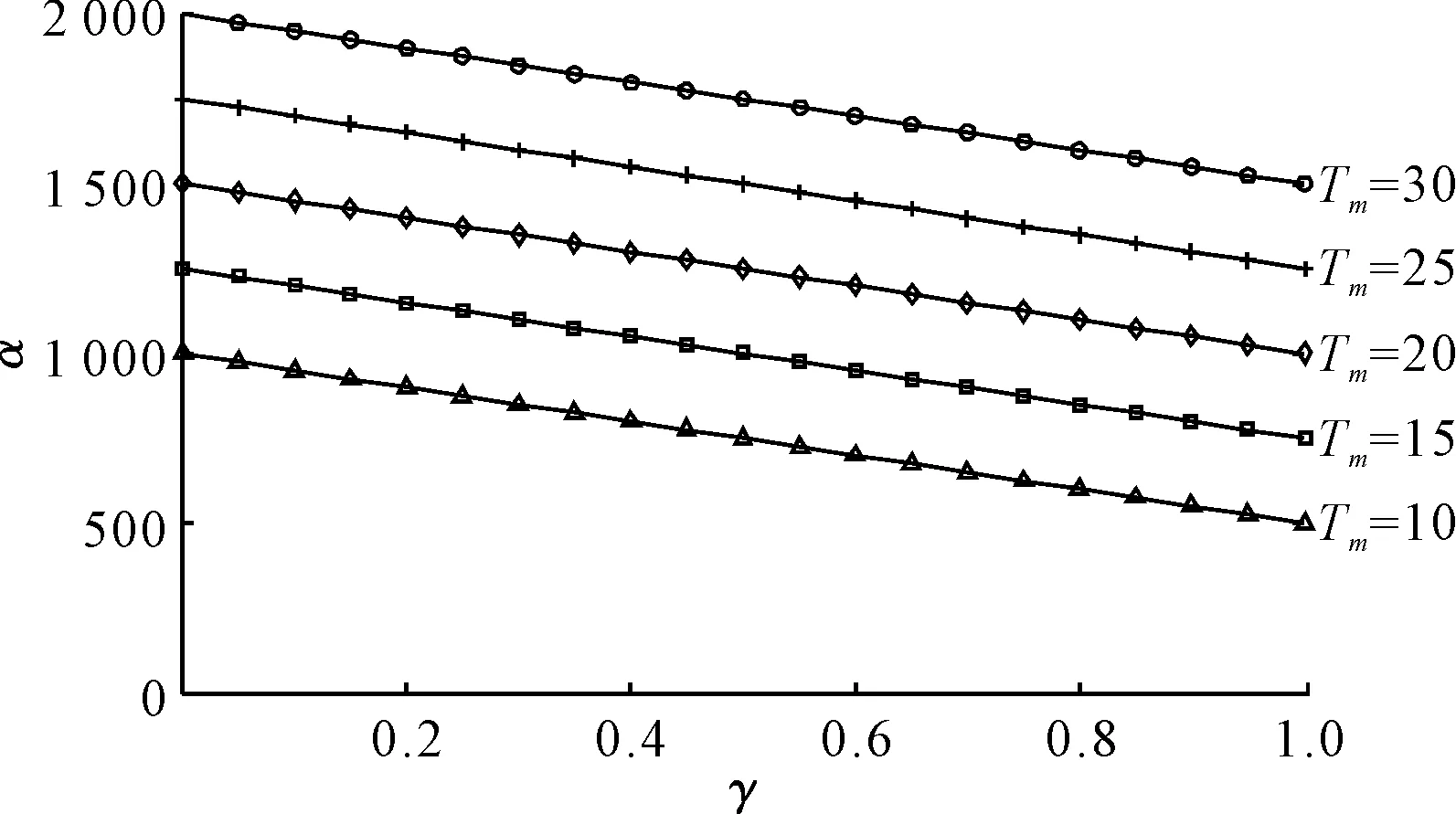
图4 项目资本金比例γ对α的影响

图5 可变成本对努力系数敏感性λ对α的影响

图6 工期受努力系数反应程度η对α的影响

图7 工期对可变成本反应程度μ对α影响

通过以上参数变动对于最优努力程度的影响，可得出如下推论。

推论4最优努力程度α与项目资本金γ、可变成本对努力系数敏感性λ呈负相关关系。当γ、λ增大时，α反而减小；当γ、λ减小时，α反而增大。

推论5最优努力程度α与工期受努力系数反应程度η呈正相关关系。当η增大时，α随之增大；当η减小时，α随之减小。

推论6最优努力程度α与特许经营期Tm呈正相关关系。Tm增大时，α随之增大。因此，对于特许经营期较长的项目，应提高社会资本方准入门槛，保证努力程度。

4.3 参数变动对于政府方最优收益的影响

股比k对政府方收益的影响如图8所示，可以看出股比与政府方收益存在着反U型曲线关系，存在最优的股比使得政府方项目收益达到最高。同时，随着特许经营期的延长，图8中反U型曲线会越来越陡峭，这意味着股比对政府方收益影响的边际效会逐渐递增。

图8 股比k对政府方收益g的影响

图9 股比k对社会资本方收益c的影响

4.4 参数变动对于社会资本方最优收益的影响

股比k对社会资本方收益的影响如图9所示，可以看出对于社会资本方而言，股权比例的提高，可以提高项目整体收益。同时，随着特许经营期的延长，图9中单调递增曲线会更加陡峭，这意味着股比对社会资本方收益影响的边际效会逐渐递增。

5 案例分析

以湖南长沙市地下综合管廊PPP项目为例进行分析，该项目建设总投资约为39.95亿元，建设管廊总里程约为42.69 km。项目合作期限为28年，其中建设期3年，运营维护期25年。先建管廊建设里程约为17.38 km，建设投资约为17.04亿元，采用“转让—运营—移交”形式(实物出资部分除外)有偿转让给PPP项目公司进行运营管理；后建管廊建设里程约为25.31 km，建设投资约为22.91亿元，采用“建设—运营—移交”形式，由PPP项目公司负责全部的投融资、施工图设计、建设运营及移交工作。

该项目的项目资本金为项目总投资的30%(约11.99亿元)，由政府方及社会股东参照股权比例分别出资，其余资金通过银行贷款等债务融资方式筹集。

将现有数据及参数估计值代入模型：

M=R(γ-1)[1+(Tm+Tf)i]+Tmπ+

N=[R(1-γ)ηi+Tmf]×

最优股比k*为:

由项目公司设立情况可知，政府方指定出资机构持股34%，社会资本方持股66%。与求解的社会资本方股权比例k=0.64相近。因此，项目由社会资本方控股，可达到较好收益情况。

政府方依据长沙市相关国资监管制度体系依法履行法人治理、业绩考核、薪酬管理、预算管理等职责，与社会资本方共同出资设立项目公司。双方股东分别按各自股权比例享有项目公司收益分红。

6 结论

笔者通过对政府方与社会资本方股权博弈进行建模分析，构建了Stackelberg动态博弈模型，并分析了各参数变化对于结果的影响，结合研究结果给出以下投资建议：①当项目特许经营期较长或利润波动明显时，为达到政府收益最大化，政府方作为发起人应掌握控股权。反之，社会资本方应掌握控股权。②受双方博弈影响，社会资本方的股权比例存在一定范围内时可达到最优收益。③政府方与社会资本方股权分配差异不宜过大。当股权比例较为极端时，尤其对于政府方而言，收益会受到较为严重的影响。

在后续研究工作中，笔者将考虑以下因素对股权结构的影响： ①社会资本准入条件。在PPP项目前期，应谨慎选择合作的社会资本方。尤其是对于特许经营期较长的项目，应提高准入门槛，保证社会资本方努力程度，推进项目进程。②PPP项目补偿机制。政府方应创造良好的融资环境，建立多种利益补偿机制，有效保障合理的投资收益，激发社会资本方投资和建设热情。③行为因素。行为经济学研究表明，决策者往往是有限理性的经济人。故后续可开展行为实验，考察信任、公平、损失厌恶等行为因素是否会导致双方决策偏离均衡解，从而为研究法律制度不完善、公私双方地位不平等、项目信息不透明等因素打下基础。