基于改进KNN算法的手写数字识别研究

胡君萍，傅科学

(武汉理工大学 信息工程学院，湖北 武汉 430070)

目前，仍有大量的手写数字单据需要录入计算机进行管理，比如物流行业中手写快递单据、银行业的手写支票和汇款单、公司账本等，如果能进行智能化的手写数字识别，则可以节省大量的人力。手写数字识别方法从原理上大致可以分为基于统计特征分类、基于结构特征分类、基于神经网络三大类算法[1-4]。K最近邻(k-nearest neighbors，KNN)算法是基于统计特征进行分类的人工智能算法，简单易懂，对系统要求低，因此笔者选取该算法对手写数字进行识别研究。Python是一种解释型、面向对象、动态的高级脚本语言[5]，其通过编译器运行，可以实现快速的机器学习和人工智能算法的实现，笔者用Python作为编程语言。

1 KNN算法原理

KNN算法是通过选择分类集合中与待分类样本最相似的K个样本值，通过决策得出待分类样本的类别。KNN算法属于分类与逻辑回归算法[6]，KNN只存在前向传播过程，不存在学习的过程，是机器学习中简单有效的分类算法。将分类集合替换为手写数字集合，即可用于手写数字识别。

KNN算法实现的整个过程中有四大核心点：①分类集合的选择；②K值的选择；③向量距离度量规则；④决策方案。其中，训练数据集的选择和K值的选择需要综合考量，过大会降低整个算法实现的效率，过小会影响识别的精度；向量距离度量规则用来确定待分类样本与分类集合中样本的相似度；而决策方案用来确定待分类样本属于哪个类别，优秀的决策方案可以极大地提高分类的准确率。根据KNN算法原理，用KNN实现样本分类与识别的程序流程图如图1所示。

图1 KNN算法流程图

2 传统KNN算法在手写数字识别中的实现

2.1 手写数据集的选择

手写数字识别算法的研究需要有好的手写数字集(即分类集合)进行训练和测试，目前主要有3种数据集：USPS、UCI和MNIST。

USPS即美国邮政服务手写数字识别库，该手写数字样本库中共有9 298个样本，其中7 291个样本组成训练集，2 007个样本组成测试集，所有样本采集于邮政记录员的笔迹。

UCI是用于笔交互的手写数字识别库，该数据集采集于44位不同行业人员的手写笔迹，共计250个，训练集和测试集自行分配。

MNIST手写数据集是由Google实验室、纽约大学柯朗研究所及微软研究院整理了不同年龄段人的手写数字构成的集合[7]，包含60 000个训练集和10 000个测试集。MNIST数据集中部分手写数字图片如图2所示。

图2 训练集前28张手写数字图

手写数字识别研究需要具有泛化性能和更高的准确率，因此选择数据人员类型多样化和数据量大的MNIST数据集作为本研究进行测试和训练的数据集。

2.2 图像预处理

采用KNN实现手写数字识别，首先需要将MNIST数据集标准化为KNN需要的格式，因此需要对MNIST数据集进行预处理，即读取MNIST数据集，并将其转化为1×784的向量，MNIST数据集中图像训练数据为60 000条，图像测试数据为10 000条，因此训练数据可形成60 000×784的矩阵，测试数据可形成10 000×784的矩阵。

为了更好地提取数字的结构特征和统计特征，一般还需要对图片数据进行归一化和二值化处理。假设r(x,y)是位于图像中坐标(x,y)处的原始灰度值，c(x,y)是位于图像中坐标(x,y)处的归一化灰度值，b(x,y)是位于图像中坐标(x,y)处的二值化值，maxg代表图像中的最大灰度值，ming代表最小灰度值，其表达式分别如式(1)和式(2)所示。归一化公式和二值化公式分别如式(3)和式(4)所示。

(1)

(2)

(3)

(4)

MNIST数据集的标签采用长度为10的向量表示0～9,共10个种类。该向量由9个0.1和1个0.9组成，其中0.9在向量中的编号代表此标签的值，用一个长度为10的向量作为一个输出标签。

2.3 传统KNN算法的实现

(1)选择向量距离度量规则。在上述图像预处理中，手写数字已经转化为向量，笔者使用欧氏距离作为距离度量规则[8]，欧氏距离越小，则说明相似度越大。

在二维空间中，假设A点的坐标为(x1,y1)，B点的坐标为(x2,y2)，则AB两点欧式距离dAB的计算公式为：

(5)

在N维空间中，假设向量A为(x11,x12,…,x1n)，向量B为(x21,x22,…,x2n)，则向量AB的欧式距离dAB的计算公式为：

(6)

(2)训练数据集的选择。MNIST数据集有60 000条训练数据，如果全部进行欧式距离的计算，会占用极大的计算机资源，同时时间和复杂度剧增，效率较低，因此选择其中的10 000条作为训练的样本实例进行欧式距离的计算。

(3)K值的选择。当K值过小时，则整体的决策流程迅速，但出错的概率较大；当K值过大时，则整体的决策复杂，时间和空间复杂度使识别效率降低。阿拉伯数字共计10个种类，选择K=10，可以将10种数字容纳到邻近的K类中，有利于提高准确率，同时复杂度也可以接受。

(4)决策方案的选择。笔者将K个数据中出现次数最多的分类值作为最终的预测值。待识别的手写数字通过欧式距离计算，找到10个最相似的MINIST数据集中的样本，如果值为2的样本最多，则待识别的手写数字识别为2。

2.4 传统KNN算法弊端分析

传统KNN算法作为一种无参的简单有效的分类方法，在基于统计特征的机器学习中具有较好的表现。虽然存在上述优点，但是也存在以下缺陷。

(1)手写数字图像具有高维度特征，使得运算较复杂，KNN又无法很好地实现特征提取，对分类结果起决定性作用的维度往往远小于原输入维度，对那些无法起决定性作用的特征，一般会成为噪声，影响分类结果。

(2)不同人的手写数字差异性较大，即MNIST数据集中同一类别的数字差别大，可能出现训练集中较多其他类别的图像进入K-最近邻范围，较少同一类别的图像进入K-最近邻范围，导致分类结果错误，其模型示意如图3所示。由图3可知，待分类样本的值应为1，且分类集合中部分为1的样本值也很靠近待分类样本，但是由于在K-最近邻范围内存在大量的样本值为7的数据，导致最终的分类结果错误地识别为7。

图3 传统KNN识别错误模型图

3 基于PCA降维和距离权重统计的改进KNN方法

针对传统KNN在手写数字识别中存在的问题，经过研究采取如下两种措施进行改进：①针对第一个缺陷，利用主成分分析法(principal component analysis，PCA)[9]提取高维向量中的主要特征，实现降维。②针对第二个缺陷，将基于距离的权重统计方法应用于KNN算法中，在K-最近邻范围，距离越近则赋于其的权重越高，这样可以弥补手写数字不规范及训练样本中不同类数据相似度较高带来的识别错误问题。

3.1 PCA降维提高识别速度

3.1.1 PCA降维方法

PCA的目的就是在保证信息熵最大的情况下，使数据的维度尽可能地降低，使得计算过程中的运算量减小。PCA就是在高维特征空间中，选择合适的投影空间，计算高维向量在投影空间中的投影向量，即得到降维数据。具体的PCA降维过程如下：

(1)对输入的数据进行预处理，即按照式(7)进行均值归一化处理。

(7)

(2)计算协方差矩阵Σ。

(8)

(3)采用奇异值分解函数计算Σ的特征值和特征向量。

Σ=USVT

(9)

式中：U为左奇异向量，用于压缩行特征；S为奇异值；V为右奇异向量，用于压缩列特征。

(4)对输入的数据按照式(10)进行降维。

Zi=[u1，u2，…，uK]TXi

(10)

式中：ui为特征向量中前K列列向量；Zi为降维后的数据。

经过上述的处理过程，可以有效消除手写数字图像中的噪声，更加凸显图像数据与标签值之间的对应关系，同时压缩了特征空间，提高了执行效率。

3.1.2 PCA的特征维度选择

PCA的特征维度选择对整个算法执行有重大影响，只有采用合适的维度，才能够既降低计算时间，又不影响算法的准确度。为此，笔者首先检测PCA特征维度选择对整个算法的影响，通过不断地调用执行PCA算法的程序，并在每次迭代中对特征维度增加1，得到PCA维度与算法识别准确率的关系，如图4所示。

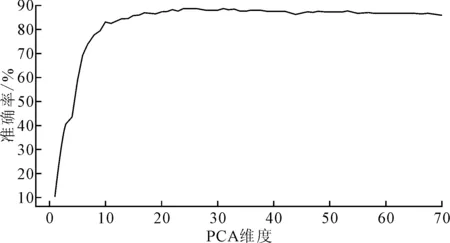
图4 PCA维度选择对算法结果的影响

由图4可知，当PCA特征维度选择在20以下时，识别的准确率受到明显影响，在PCA维度为30时，其准确率已经接近最高，说明已经有效地提取了手写数字图片的主要特征，再继续增加PCA特征维度已经对准确率的提升没有太大的影响，反而增加了很多时间和空间上的消耗。因此，改进KNN算法的PCA特征维度选择为30。

3.2 距离权重统计方法提高识别精度

距离权重统计的目的是为了提高分类结果的准确率，在传统KNN算法中，已经计算了待分类数据与训练数据之间的欧氏距离，再按式(11)计算距离权重Wi。

(11)

其中，di为待测样本与第i个近邻的距离；d1为K近邻中最近数据的距离；dK为K近邻中最远数据的距离。

对上述计算得到的距离权重按照标签值进行归类叠加，叠加距离权重越大，说明待识别数字属于此类别的可能性越大。

3.3 改进KNN算法流程的设计

改进KNN算法流程：①首先读入数据，形成特征矩阵。②运用PCA方法对手写数字图像特征进行降维处理。③采用传统的KNN算法，选择距离最近的前K条训练数据。④对选出的前K条训练数据进行距离权重统计，选择叠加权重最大的类别，为待分类数据的类别。

在传统KNN算法的基础上，加入PCA降维和距离权重统计两种方法组合成改进的KNN算法，并应用于手写数字识别中，其算法流程如图5所示。

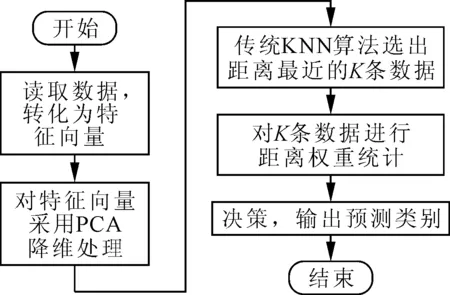
图5 改进KNN算法流程图

4 实验结果及分析

选定手写数字集MNIST中样本数据集数量为3 000，K值为10，PCA维度为30，选择MNIST中测试集的10 000条测试数据，用Python编程对传统KNN算法和改进KNN算法进行测试，得到传统KNN算法和改进KNN算法的准确率和全部预测完10 000条测试数据所用时间，如表1所示。

表1 基于KNN算法的测试结果对比表

由表1可知，改进的KNN算法在预测的准确率上提高了3.12%，准确率达到了93.86%，但识别时间不到传统KNN算法的2%，说明改进的KNN算法的执行效率得到极大提高，节约了时间和空间。虽然特征不够明显的数据因书写不规范的原因仍然存在识别错误的情况，但是相对于传统KNN算法而言，从准确率对比上可以看出，部分数据因手写不规范引发的分类误差已经得到了明显的改善。

基于上述测试结果，统计得到改进KNN算法的识别错误数据的分布，如图6所示。由图6可知，错误主要发生在3和8之间，因为由不同的人书写的数字3在外貌描述上与8更接近，导致改进KNN算法识别错误。

图6 改进KNN算法的识别错误统计图

在人工智能领域，基于神经网络算法比基于统计特征分类的KNN算法有更好的识别准确度。为此，笔者也对基于卷积神经网络算法和基于BP神经网络的算法[10]在手写数字集MNIST上进行实验，同样，选定样本数据集数量为3 000，选择测试集中的10 000条测试数据，实验得到两种算法的训练耗时、预测耗时及准确率，结果如表2所示。由表2可知，改进的KNN算法虽然相对于传统KNN算法的准确率提高了3.12%，但相对于神经网络算法，尤其是卷积神经网络算法，仍然有差距。所以，类别差异小的分类与识别宜选择卷积神经网络算法，改进KNN算法复杂度低，可用于类别之间差异大的分类与识别，如电影分类、网页内容分类、话题分类[11]等。

表2 BP神经网络和卷积神经网络算法测试结果

5 结论

在传统KNN算法的基础上，采用PCA降维方法和距离权重统计进行算法改进，得到的改进KNN算法可以极大地提高手写数字识别的效率，并且提高了识别准确率。改进KNN算法相对于卷积神经网络算法，虽在识别精度上有差距，但复杂度低，更适用于类别之间差异大的分类与识别。