受启发的回溯搜索算法在优化问题中的应用
李媛媛,贾志成,*,陈 雷,郭艳菊
(1.河北工业大学 电子信息工程学院,天津300401;2.天津商业大学 信息工程学院,天津300134;3.天津大学 精密仪器与光电子工程学院,天津300072)
0 引言
回溯搜索(Backtracking Search,BS)算法是Pinar Ciricioglu[1]于2013年提出的一种群体智能优化算法。BS算法与粒子群(PSO)算法[2],差分(DE)算法[3],生物地理优化(BBO)算法[4]和人工蜂群(ABC)算法[5]等元启发式优化算法一样,具有相似的特点:算法结构比较简单、寻优过程易于实现、方程涉及参数较少、无需梯度信息等。一经提出便吸引到了大量学者前来研究,并且在风力涡轮机功率曲线模型[6]、经济排放调度问题[7]及表面波分析[8]等众多领域得到了广泛的应用。
然而,与其他智能算法类似,较慢的收敛速度和较低的搜索精度也是BS算法急需解决的问题,限制了BS算法在实际中的应用。对此,学者们提出了多种改进策略来优化BS算法的性能。文献[9]通过改进算法的搜索方程,提高了BS算法的优化性能。文献[10]从扰动方式角度出发,得到了一个高效变异尺度系数并将其应用于BS算法中,另外,将贪婪性添加于交叉策略,从而优化了BS算法的性能。文献[11]为避免出现早熟收敛,在变异策略中添加了一种选择机制以增加全局搜索能力。但是,在处理过于复杂的问题时,改进的算法依然在收敛速度和早熟收敛两方面难以取得平衡。
为了提高BS算法的收敛速度及避免早熟现象,本文对影响这一现象的主要因素即算法的搜索方程进行了分析与改进。在贪婪机制的启发下,提出了一个具有较强开发能力的新搜索方程,它是在最优解的引导下产生一个新的候选解以便算法更快地收敛于全局最优位置。为了避免BS算法陷于局部极值点,采取了在BS算法的搜索方程中添加扰动算子的策略。仿真实验表明结合两种搜索方程的BS算法能够有效地提高优化性能和优化效率。
1 回溯搜索算法
BS算法是最近提出的一种新型的群体智能优化算法,通过模拟生物进化的行为而搭建的一种随机模型。该算法的基本理论简单易懂,现将BS算法的基本原理简述如下:
BS算法的描述概括为5个部分:初始化、选择-1、变异、交叉和选择-2。BS算法的简单流程图如图1所示。
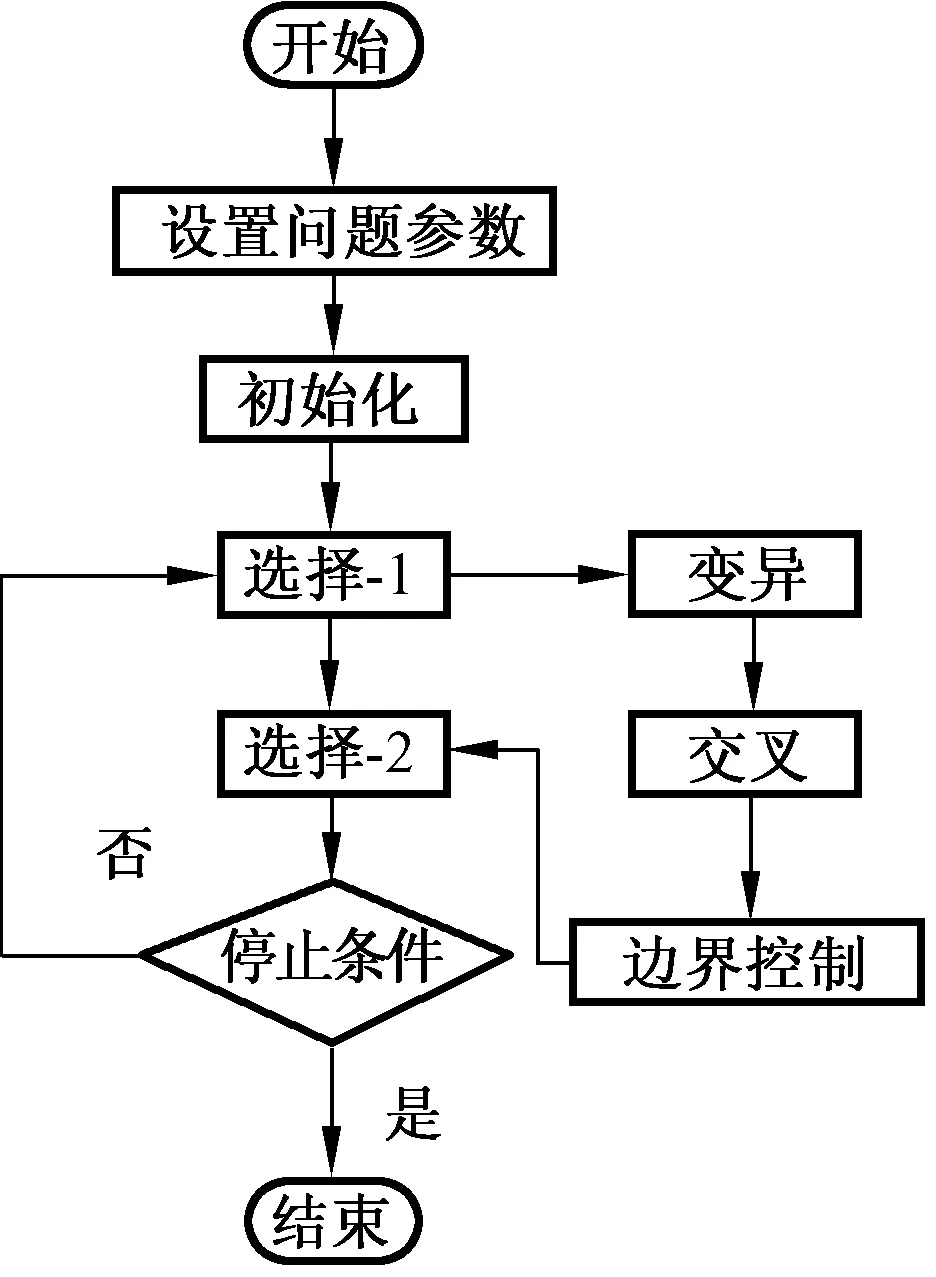
图1 BS算法的简单流程图
Fig.1 Simple flow chart of BS algorithm
1)初始化
BS算法和其他群体智能优化算法一样,在设置好问题参数后需对种群进行初始化操作,即根据所求的优化问题形成一个可行的解空间,并在生成的解空间里对种群进行初始化操作,唯一不同之处在于BS算法需完成双种群P和oldP的初始化操作,初始化操作如下式:
(1)
式中,Pi={Pi,1,Pi,2,…,Pi,D}代表原始种群P的每一个粒子,oldPi={oldPi,1,oldPi,2,…,oldPi,D}代表历史种群oldP的每个粒子,i=1,2,…,NP为种群中每个粒子的编号,NP为种群中所有粒子的总数,j=1,2,…,D为所求优化问题的解维数,D为所求优化问题的最大解维数,U为随机均匀分布函数。
2)选择-1
BS算法在选择-1阶段主要是针对历史种群oldP进行选择,如下式:
ifa (2) 式中,a,b为[0,1]均匀分布随机数。在每次迭代过程中,由a和b的大小决定历史种群oldP是否更新。若满足a 3)变异 BS的变异过程是在原始种群P和历史种群oldP之间进行变异操作。以原始种群P为中心,历史种群oldP为搜索方向,产生变异种群Mutant,即 Mutant=P+R·(oldP-P), (3) 式中,R用来控制产生的新搜索方向的前进幅度,其产生方法为R=3·rand,rand为[0,1]均匀分布随机数。 4)交叉 BS的交叉策略由两种交叉策略组成,在交叉过程中等概率调用两种交叉策略。在交叉策略一中,交叉长度始n终被赋值为1;在交叉策略二中,交叉长度n是一个面向每一个粒子所产生的随机数,如下式: n(i)=[mixrate·rang·D], (4) 式中,mixrate是交叉概率。交叉后产生的新种群粒子Ci有可能超出搜索的解空间,需进行边界处理,即在优化问题的解空间内由式(1)产生一个随机粒子Pi,用Pi取代超出优化问题的解空间范围内的新种群粒子Ci。经过交叉和边界处理后,最终产生一个新种群C。 5)选择-2 在BS的选择-2操作中,采用贪婪机制选取更优种群保留下来,该贪婪机制通过比较原始种群粒子Pi和新种群粒子Ci的适应度值来实现。若新种群粒子Ci的适应度值优于原始种群粒子Pi的适应度值,则将新种群粒子Ci取代原始种群粒子Pi;否则,继续保留原始种群粒子Pi。如下式: (5) 式中,fit是适应度函数,选择-2操作的完成标志着进化过程的一次优化搜索,重复进行上述优化搜索过程实现多次优化搜索,最终得到全局最优种群粒子Pbest。 由1节可知,BS算法是以种群为对象进行变异和交叉操作,此做法不可避免地忽视了种群中的个体所具有的优化能力。受贪婪机制的启发,本文提出一个全新的搜索方程以保证更具优化能力的粒子来进行变异和交叉操作,而不是种群间盲目地进行此操作。此策略通过衡量种群中每一个粒子在所有粒子当中优化能力水平,将处于平均优化能力水平以下的粒子淘汰,用当前种群中最具优化能力的粒子取代。粒子优化能力水平的衡量标准参照种群中所有粒子的平均适应度值afit的大小,如下所示: (6) 本文所提出的用以生成具有较高的优化能力的粒子的全新搜索方程如下所示: Pi=bestPi+R·(oldP-bestPi)afit (7) 式中,bsetPi为当前种群中最优粒子,引导种群向更优的方向搜索以保证种群粒子的搜索能力水平。 采用了全新的搜索方程的IBS算法不仅将处于劣势地位的粒子淘汰,还在当前种群最优粒子的引导下生成了更具优化能力的粒子来取代劣势粒子。与BS算法相比,IBS算法具有更精准的寻优方向和更强大的开发优秀粒子的能力,这不仅保证了解的质量还加快了算法的收敛速度。 标准BS算法由于只有一个控制参数即历史种群,来控制种群搜索方向,在处理较复杂优化问题时,往往会陷入局部最优。虽然在算法执行的初期具有较好的探索能力,然而在后期算法效果并不理想,出现收敛速度减慢,对于较复杂的高峰函数,甚至搜索不到最优解。受简化而高效的粒子群优化算法[12],为摆脱局部极值而添加扰动算子的启发,本文提出了一种改进的回溯搜索算法,即在搜索方程中添加扰动算子。 文献[12]添加的扰动算子为 pg=rtg>Tgpg, (8) 本文在文献[12]的基础上提出了带扰动算子的方程,如下所示: M=P+R·(r·oldP-P), (9) 式中,r为扰动算子。当出现早熟收敛现象时,改进的搜索方程通过扰动算子操作来更新种群,使算法快速跳出局部最优区域。 BS作为一种新生的群体智能优化算法,已比其他的经典群体智能优化算法取得了较佳的收敛速度和收敛精度,但是在处理复杂的实际优化问题时,BS算法的优化过程还需进一步提高。因此,本文提出了一种改进的回溯搜索(Improved Backtracking Search,IBS)算法,即在其寻优过程中将全新的搜索方程和改进的搜索方程配合使用。现将IBS算法的具体步骤介绍如下: Step1:设置种群中所有粒子的总数为NP,通过式(1)初始化原始种群P和历史种群oldP。 Step2:计算初始化原始种群P中每一个粒子的适应度值,得到初始化原始种群P中的最优粒子。 Step3:通过式(9)和式(4)对种群中的粒子进行变异和交叉操作,产生新的种群M,计算新种群M中每一个粒子的适应度值,和初始化原始种群中P每一个粒子的适应度值比较,选择更优的粒子更新搜索种群P,并得到当前最优粒子。 Step4:对搜索种群P进行淘汰选择,通过式(6)计算搜索种群P中所有粒子的平均适应度值和每个粒子的适应度值,并把它们进行比较。依据式(7)产生一个新的粒子取代淘汰的粒子,再一次更新搜索种群P。 Step5:计算搜索种群P中每一个粒子的适应度值,得到搜索种群P中的最优粒子,与原始种群P中的最优粒子做比较,更新当前全局最优种群粒子Pbest及对应的适应度值。 Step6:检查是否满足停止条件。若满足条件,则停止迭代,并输出全局最优种群粒子Pbest及对应的适应度值。否则,返回Step3。 为了测试本文提出的IBS算法的性能,进行仿真实验的测试函数从文献[13]中选取。表1中列出了6个常用于优化算法比较的标准测试函数。其中,f1~f3为单峰函数,优化算法在对单峰函数测试时比较容易找到全局最优点,故单峰函数主要用来检测算法的收敛速度。f4~f6为多峰函数,多峰函数存在许多局部极值点导致算法在搜索过程中很容易陷入局部最优,故多峰函数主要用来检测算法跳出局部极值点的能力。优化这些测试函数的难度会随着它们的维数、自变量范围的增加而增加。本文选取较为苛刻的实验参数,具体参数设置为:种群粒子总数为30,优化问题维数为30,进化迭代次数为500或1 000。为使实验结果更具有说服力,所有的实验结果均采用独立运行30次后的平均值。本实验分成3个部分进行:1)在迭代次数一定的条件下,测试算法的收敛速度和收敛精度;2)在收敛精度一定的条件下,测试算法的迭代次数;3)一般条件下,与其他算法的性能比较。 表1 测试函数 函数名公式搜索范围最小值收敛精度Spheref1(X)=∑ni=1x2i[-100,100]010-21Schwefel 2.21f2(X)=max|xi|,1⩽i⩽n{}[-10,10]010-1Schwefel 2.22f3(X)=∑ni=1|xi|+Πni=1|xi|[-10,10]010-13Ackleyf4(X)=-20exp-0.21n∑ni=1x2i()-exp1n∑ni=1cos(2πx1)()+20+e[-32,32]010-12Griewankf5(X)=14 000∑ni=1x2i-Πni=1cosxii()+1[-600,600]010-6Rastriginf6(X)=∑ni=1[x2i-10cos(2πxi)+10][-5.12,5.12]010-2 3.2.1 测试算法的收敛速度和收敛精度 图2给出了BS和IBS算法在迭代次数一定时,它们各自达到的收敛速度和收敛精度的实验结果。其中,图2给出了测试函数f1~f6的适应度收敛曲线,横坐标表示进化迭代次数,纵坐标表示测试函数的适应度。为了方便收敛曲线的观察,本文采用以10为底的对数作为函数的适应度值。由图2可以看出,在D=30,迭代次数均为1 000次的条件下,IBS比BS算法的收敛速度明显快出很多。特别地,图2(e)和(f)在保证收敛速度的情况下很快地找到了全局最优值。这说明强强联合的两个搜索方程在收敛速度和收敛精度上获得了平衡,同时也说明了本文改进的IBS算法在实用性方面性能良好。 图2 BS和IBS算法的收敛曲线图 3.2.2 测试算法的迭代次数 参照表1中给定的收敛精度,BS和IBS算法的测试结果如表2所示,其中,平均迭代次数、最小迭代次数、最大迭代次数、成功率[12]和期望迭代次数[12]分别是经过30次独立运行后的得到的结果。成功率=达到固定精度的运行次数/总实验次数,期望迭代次数=种群粒子总数×平均迭代次数/成功率,“∞”表示Expected iterations为无穷大。由表2可以看出,除了f2以外,本文改进的IBS算法的成功率均达到了100%,并且在收敛精度一定的条件下,平均迭代次数均小于500。这说明本文提出的IBS算法具有非常高的优化性能。 表2 指定收敛精度下的迭代次数 函数算法迭代次数平均值最小值最大值成功率期望迭代次数f1BS5005005000∞IBS418361480112 526f2BS5005005000∞IBS128335000.966 73 978f3BS5005005000∞IBS417363485112 504f4BS5005005000∞IBS430361484112 899f5BS5005005000∞IBS26517937917 943f6BS5005005000∞IBS27214145718 159 3.2.3 与其他算法的性能比较 为进一步展示IBS的先进性,将ABC、差分搜索(DS)算法、改进的人工蜂群(MABC)算法和IBS算法的结果进行比较,如图3所示。将以上4种算法的参数都设置成:种群中所有粒子的总数为30,所求优化问题的最大解维数为30,进化迭代次数为1 000。由图3可以很明显地看出,在相同实验条件下,本文提出的IBS算法比其他算法具有更快的收敛速度和更高的收敛精度。 受贪婪机制和粒子群算法的启发,本文分别提出了一个全新的搜索方程和改进了一个原有的搜索方程。在算法的实际优化过程中,两个搜索方程的配合使用平衡了算法的开发能力和探索能力,同时有效的解决了BS算法在收敛速度和收敛精度两方面效果不佳的问题。对测试函数寻优的实验结果表明,本文IBS算法能够在较低迭代次数下很快趋近全局最佳值,甚至找到了最小值。 此外,将本文所改进的算法应用到通信、科技和工业等领域,是下一步需要研究的方向。 图3 ABC、DSA、MABC和IBS算法的收敛曲线图2 受启发的回溯搜索算法
2.1 全新的搜索方程
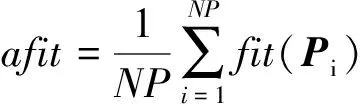
2.2 改进的搜索方程

2.3 算法的实现步骤
3 仿真实验
3.1 实验设计
Tab.1 Benchmark functions
3.2 实验结果及分析
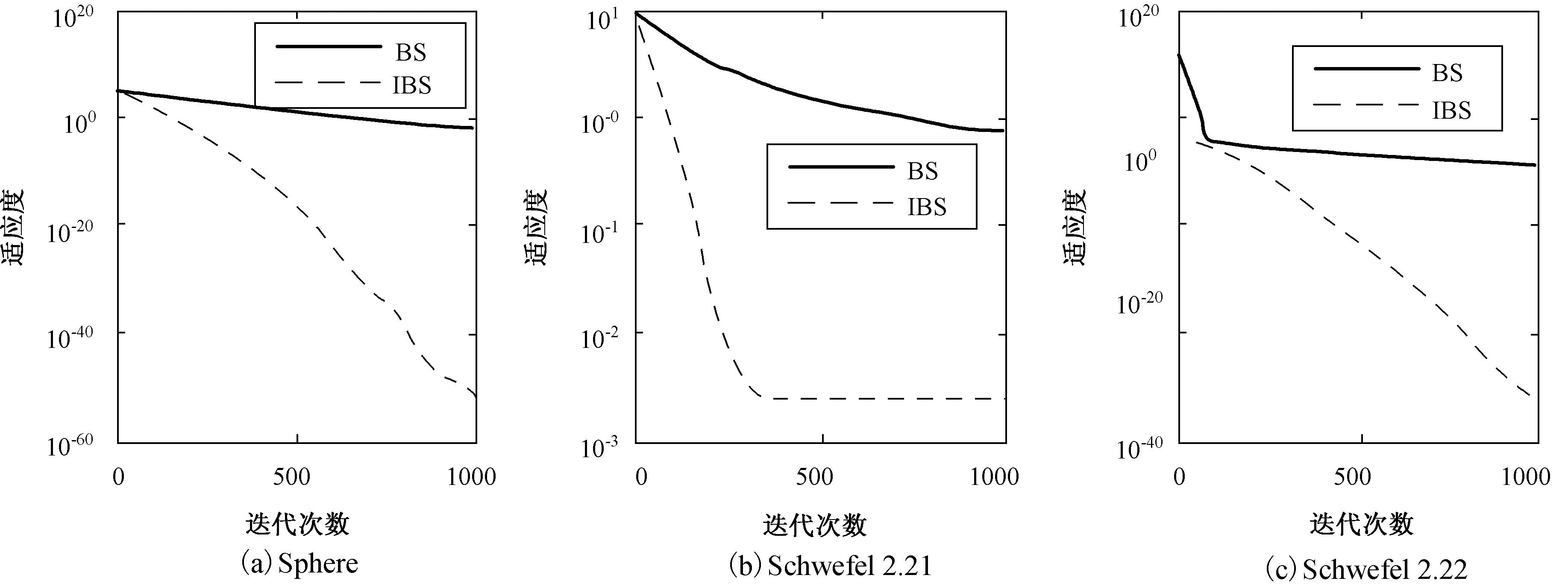
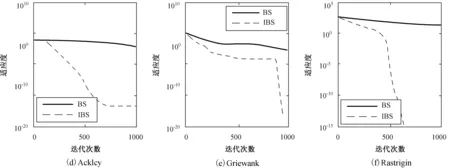
Fig.2 Convergence curves of BS and IBS algorithms
Tab.2 The number of iterations under convergence accuracy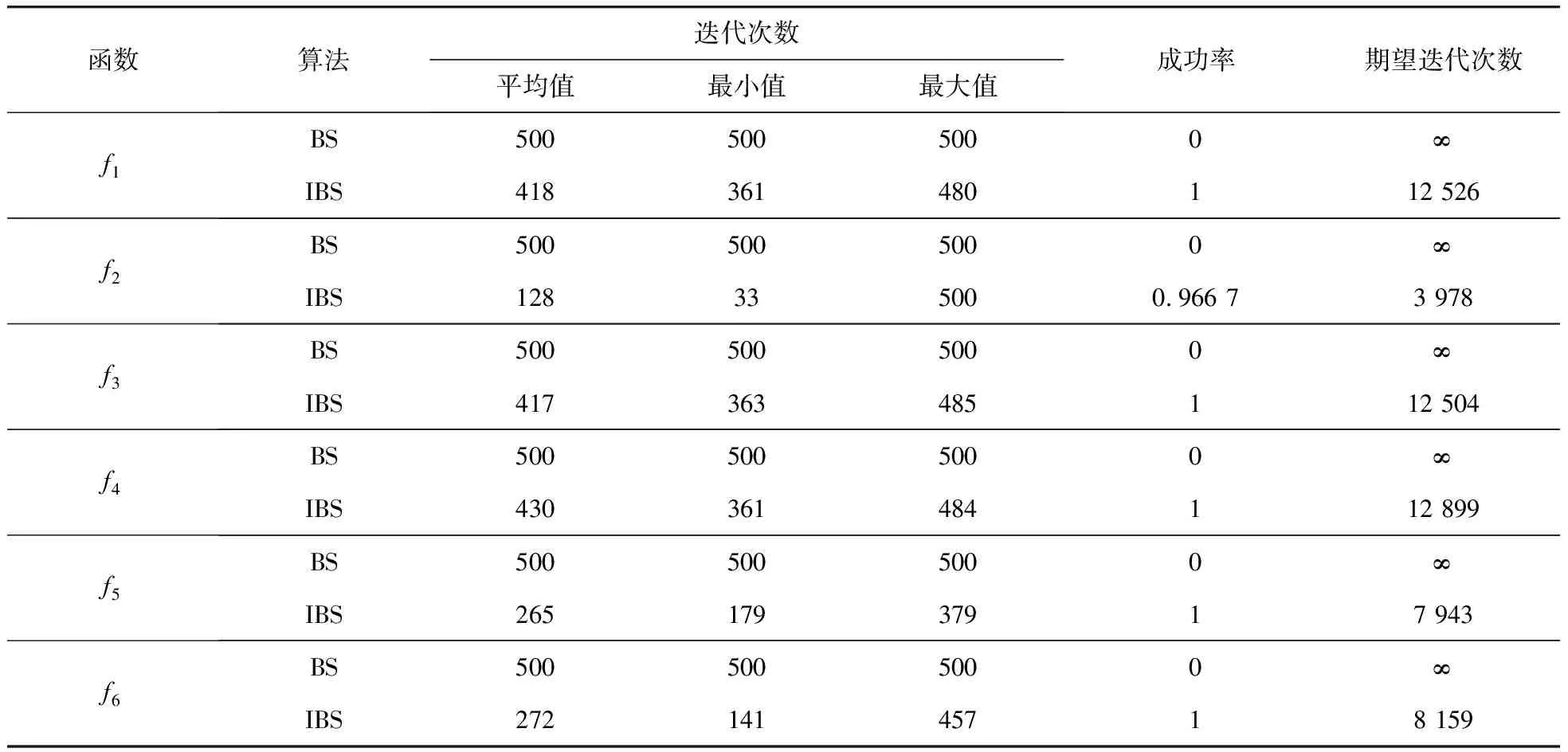
4 结论
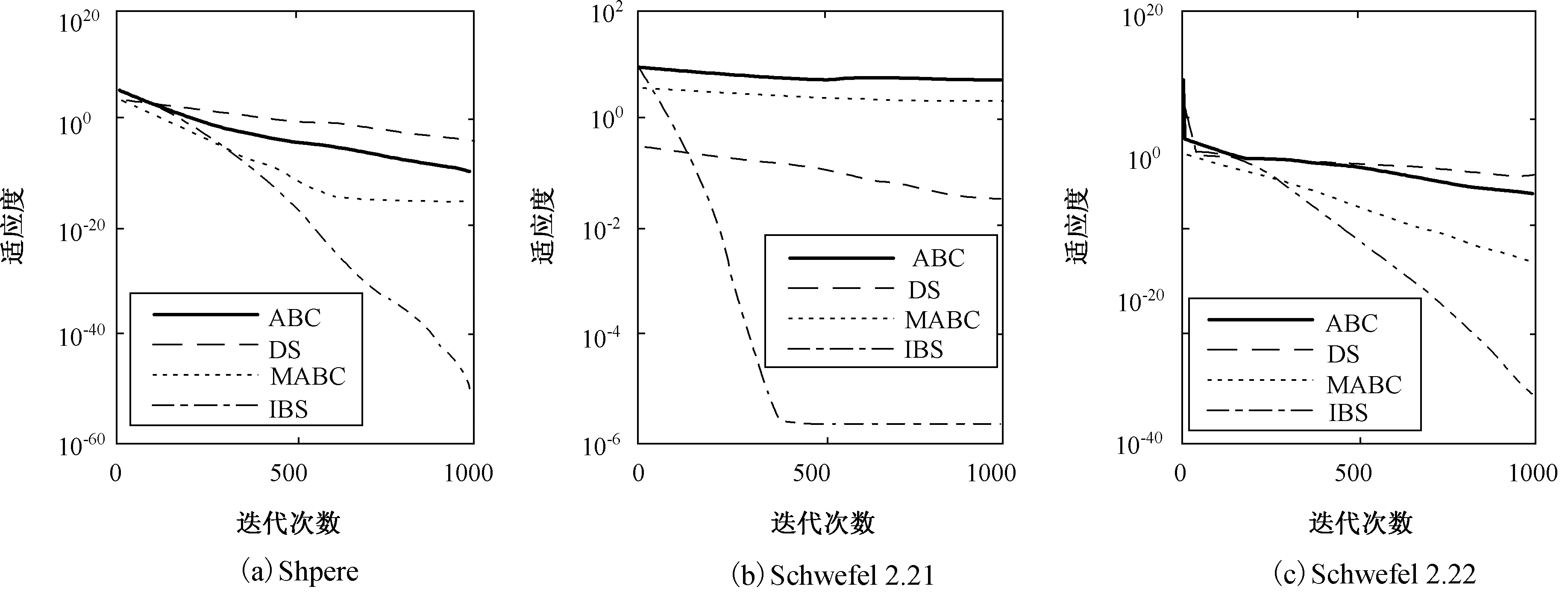
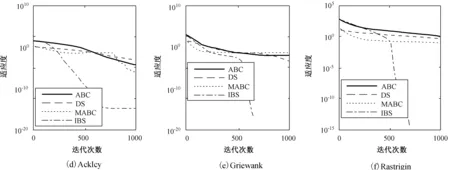
Fig.3 Convergence curves of ABC,DSA,MABC and IBS algorithms

