深空探测器动态约束规划中的外延约束过滤方法研究

姜 啸，徐 瑞，陈俐均

（1.北京航天控制仪器研究所，北京 100854；2.北京理工大学深空探测技术研究所，北京 100081；3.深空自主导航与控制工业和信息化部重点实验室，北京 100081）

引 言

深空探测器自主规划调度是利用人工智能方法，在探测器上建立远程自主系统，探测器能够合理地安排动作序列、分配星上资源，从而完成任务目标。它的目的是在不依赖或者少依赖外界信息注入或控制的情况下，能够准确地感知自身的状态和外部环境，并根据这些信息做出恰当地决策，自主地控制探测器完成各种任务。

深空探测器自主运行和传统的遥测遥控方式有很大区别[1]。传统的遥测遥控方式由地面生成指令并上传，管理探测器的运行。探测器缺乏决策能力。自主运行的探测器能够进行决策和自我管理，提高了探测器处理故障和突发事件的速度，降低了对地面站资源占用。随着我国对外太空探索的不断拓展，深空探测任务在逐年增加，提高自主运行水平是探测器发展的主要趋势。

目前，对于深空探测器的任务规划和调度的研究，通常将探测任务的调度过程和探测器活动的规划过程分别处理：①倾向于探测器任务调度问题研究，仅将探测器作为资源集合进行建模，然而并没有考虑到探测器上各活动之间的约束关系，例如为DATACHASER（STS-85 的搭载飞行试验）有效载荷开发的DCAPS（DATA-CHASER 自主规划与调度）系统[2]、法国沃瑞蒂安（Veridian）公司设计开发的GREAS（Generic Resource，Event and Activity Scheduler）系统[3]等；②倾向于探测器任务规划，通常没有考虑规划任务与探测器活动之间的约束关系，例如美国喷气推进实验室（Jet Propulsion Laboratory，JPL）开发的自主规划与调度（Autonomous Planning and Scheduling ENvironment，APSEN）系统[5-6]、连续活动规划调度执行和重规划（Continuous Activity Scheduling Planning Execution and Replanning，CASPER）系统[7]、美国国家航空航天局（National Aeronautics and Space Administration，NASA）开发的科学规划互动的知识环境软件（Scientific Planning Interactive Knowledge Environment，SPIKE）系统[8]等。这2 种方式均不利于兼顾探测器规划与调度的过程。

从探测器的实际任务生成和运行过程来看，存在大量复杂的约束，如探测任务对探测器载荷活动的需求约束、探测器活动之间的时间约束[9]、资源约束[10]等，需要对探测任务的调度过程及探测器上活动的规划过程进行融合[11-12]。但考虑到规划和调度过程的融合，需要对存在的大量复杂约束条件进行检查，不可避免地严重降低算法的效率。

深空探测器任务规划和调度方案的制定，需要考虑探测任务及探测器活动中存在的多类型复杂约束。但目前对探测器任务规划和调度的研究多采用约束较少、探测器活动规划过程与探测任务调度过程分离的方式。对于具有复杂约束的深空探测器任务，将规划和调度过程同时考虑，其约束处理和规划调度算法都具有复杂性，还需要进行深入的研究。

为解决这些问题，本文从约束处理的角度入手，将智能规划理论与约束可满足技术相结合，采用约束可满足技术提高深空探测器的约束处理能力，在可编码为约束可满足问题（Constraint Satisfaction Problem，CSP）的规划研究基础上[13]，研究多层约束规划模型中约束的动态特征，提出了基于动态约束表的外延约束快速过滤算法，根据领域信息中活动间的冲突性判定对新加入的活动进行分类，并对于约束表中变量进行一致性检查。结果表明该算法能够有效地降低约束处理中无效约束检查次数，降低问题处理过程中的算法回溯，提高规划的效率和成功率。

1 深空探测活动约束分析

在规划过程中，每当有新活动加入时，使用约束网络的一致性[13]检查新加入的活动是否满足已有部分规划的一致性。然而，在探测器任务规划过程中也可以使用探测器本身固有的先验知识进行检查，通过分析探测器的规划领域信息，设计更加高效的领域相关约束削减算法。深空探测器规划活动约束的特性包括以下2个方面。

1）规划过程中活动逐步添加

规划的过程即逐步选择活动并检查约束的过程。由活动的定义可知，星上活动一般由特定的子系统执行（例如拍照活动绑定于相机系统、加热活动绑定于温控系统），在添加活动的过程中，可以逐步计算新添加活动对约束网的影响。

2）部分活动间具有冲突关系且冲突关系仅限于本层活动之间

规划中动作可编码为CSP中的外延约束[14]，而动作的一致性由外延约束的变量决定，当满足约束一致性的相同变量取值发生冲突时，对应的约束（即活动）之间也产生了冲突关系。同时，编码为CSP的规划问题为多层变量模型，不同的变量层为具有相同变量集合的副本。同层之间由于对相同变量的赋值争夺能够产生约束冲突，而不同变量层间由于不存在变量赋值争夺，不会产生约束冲突。因此对于活动约束间冲突关系的查考，应该根据多层变量的模型逐层进行。

通过对探测器约束网络一致性检查进行约束过滤与削减的目的在于删除变量值域或约束赋值中冗余的取值，从而减小其搜索空间。约束过滤削减的前提必须保证探测任务转化的CSP 在被削减后仍为等价的CSP，即两者具有相同的变量集与相同的解集。

定义1：一个约束可满足问题P=(Z,D,C)被削减至P′ =(Z′,D′,C′)当且仅当

-P与P′等价；

-D′中每个变量值域为D中对应值域的子集；

-C′中约束的限制范围大于或者等于C，例如满足C′的所有赋值对均满足C。

其中：Z代表CSP 的变量集；D代表值域集；C代外延约束集；solution_tuple代表该CSP的约束解；符号定义P至P′的削减关系为reduce(P,P′)。

CSP的削减包括变量的值域削减和约束的可行赋值对削减两部分。在值域中一个取值是冗余的，当且仅当该取值不属于任意解集，可以通过形式化描述为

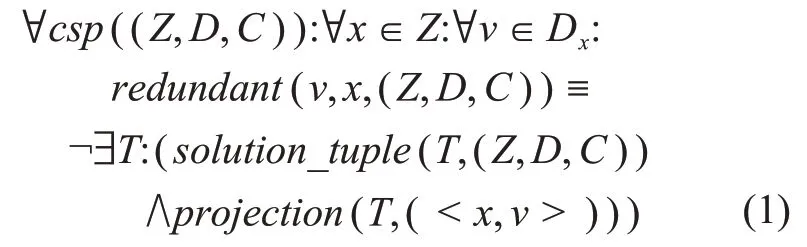
其中：projection代表解集T包含赋值对＜x,v＞。这类取值被称为“冗余的”，因为删除该取值不会影响对应CSP的任何解。

同理，约束CS中的一个赋值对是冗余的，当且仅当任何解集都不包含该赋值对

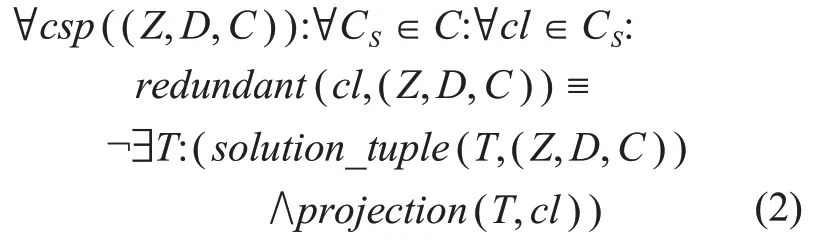
2 动态约束集构建

通过对深空探测任务模型分析可知，规划中动作之间存在明显的互斥关系（即2 个动作不能同时发生）。2个动作发生互斥/冲突分为以下3种情况。

动作冲突判定1：动作a与动作b的前提条件互斥。例如，“探测器降轨”动作的前提条件探测器位于高轨位置，而“着陆器分离电缆切割”动作需要探测器在低轨执行该操作，这个动作由于前提条件的矛盾而产生互斥，不能同时操作。

动作冲突判定2：动作a的后续状态/前提条件与动作b的前提条件/后续状态互斥。例如，动作“探测器升轨”导致探测器升至高轨位置，而动作“对行星表面拍摄”需求探测器维持在低轨位置。当探测器执行升轨动作后，升轨产生的后续状态将删除“对行星表面拍摄”动作的前提条件而导致拍摄动作不能执行，因此这2个动作不能同时执行。

动作冲突判定3：动作a与动作b的后续状态互斥。例如，“探测器降轨”动作导致探测器降至低轨位置，而“探测器升轨”动作导致探测器升至高轨位置。两个动作的前提条件可以相同，但动作执行的结果显然相互矛盾，表明由于后续状态矛盾而产生互斥不能同时操作。

对深空探测任务编码时将动作编码为约束的形式，于是动作之间的互斥转化为约束间的互斥。对于具有多层变量的CSP，每一层的约束主要由动作约束组成且这些约束存在互斥关系不能同时得到满足。因此在规划执行前需要对约束进行削减，生成内部不包含互斥关系的约束集合。

构建动态约束集主要考虑以下要点：①每个动态约束集合的编号等于对应的层号；②动态约束集内部的约束是非互斥的；③对动态约束集合进行操作时，新加入的约束不能改变已有变量的赋值关系；④由于规划中非互斥的动作可以同时执行，同层不互斥的动作约束可以同时满足。

基于上述动态约束的要点，设计构建动态约束集的算法如图1所示。

图1 动态约束集构建方法Fig.1 Construction method for dynamic constraint set

算法中layer k表示模型中的k层约束。CSP 中变量在每层中均具有相同的数据结构，在变量选择过程中，动作的前提条件总要先于后续状态进行选择。因此，约束集的层数编号可以等于前提条件变量的层数，避免了约束集分层的混乱，这里称动作的前提条件变量为驱动变量，后续状态变量为响应变量。

算法中，函数isconsisitent（）是判定当前动作约束能否加入动态约束集的核心。根据约束集构建要点，考察该约束是否与其它约束产生冲突。动作约束的驱动变量代表该动作的前提条件，若两个动作约束具有相同的驱动变量，但相同的驱动变量具有不同的赋值，可以认为这个动作的前提条件互斥。根据冲突判定1，前提条件互斥的两个动作互斥。

若两个动作约束的前提条件不发生冲突，则需要根据冲突判定2和3进一步考察。根据之前对约束表特征的研究，表头中变量可分为可变量与不变量，分别反映在相邻层之间该变量的变化情况。本文根据驱动变量的变化情况分类讨论，可分为表1 中的4 种情况。

表1 CSP中动作约束的互斥关系判定Table 1 Mutual exclusion determination of action constraints in CSP

在第1 种情况中，2 个约束中的驱动变量赋值相同，但是C1中驱动变量为可变量，C2中的驱动变量为不变量，显然对应的响应变量赋值将不会相同。这代表外延约束C1与约束C2的后续状态互斥，符合互斥判定3，因此两个约束互斥。在第2 种情况中，两个约束中的驱动变量具有可变量，因此需要进一步考虑对应的响应变量是否相同才能判定约束C1和C2是否互斥。

图2 多层结构CSP相邻层赋值示意Fig.2 Adjacent layer assignment of multilayer CSP structure

若多层结构中CSP 的赋值如图2 所示逐层进行，那么当前层只有驱动变量的赋值有可能与之前的响应变量赋值产生冲突。对于冲突判定2只需考察驱动变量即可。针对动态约束集构建要点3，若约束中的驱动变量取值范围与已有赋值对冲突，则该约束不能加入动态约束集合；反之，该约束可以加入动态约束集合。

3 基于动态约束集的快速过滤方法

3.1 算法设计

由于外延约束自身表达直观以及对可行解的枚举特性，外延约束自然地应用于配置问题（Configuration Problem）中。工程中的各种资源相容性配置问题，可以很直观通过列表的形式表达出来。例如，在k个卫星中组合选择构成星座的问题，通过列表可以根据不同标准枚举所有的可行方案。外延约束中的数据同样可以很容易通过数据库获取，数据库查询的结果有时也表现为数量表的形式。在文献[15]中介绍了数据库处理与外延约束可满足具有很紧密的理论联系。

对探测器的规划问题进行约束削减，必须保证最终的约束规划为弧一致的状态。结合CSP中的点一致与弧一致，对外延约束中的数据结构进行了定义，提出了基于动态约束集的快速表过滤算法。

在深空探测任务中，动作约束表的解集通常成组出现。例如，深空探测采样任务动作约束表如表2所示，若赋值对＜rock,rock1 ＞被剪枝后，表2 中的赋值解{1,2,5,6}由于不再满足弧一致同样需要移除约束的可行解集。

表2 探测器采样任务动作约束表Table 2 Action constraint table sampling task

针对深空任务中可行解成组出现的特性，本节设计基于动态约束集的外延约束快速过滤算法，通过将约束表中成组的可行解集集中管理，便于对算法进行搜索和回溯管理，伪代码如图3 所示。对于图3算法中scp（c）代表外延约束中组成表头的变量集合，定义table（c）为包含外延约束c中所有可行赋值解的集合。

图3 外延约束快速过滤算法伪代码Fig.3 Pseudo code for filtering algorithm of extensional constraint

对于n元变量集合以及对应的n元赋值集合τ{a1,…,an}，每一个赋值ai可以定义为ai=τ[xi]。因此一个外延约束的元数等于scp（c）的大小。

算法在第1步、第8步以及第15步通过循环检查移除未赋值变量中的冗余值域。其中第1 步中的past（P）代表当前CSP 中已被实例化（赋值）的变量集合。由于在算法开始执行时，还没有赋值对被证明为弧一致，步1、步2 中将gacValue初始化为空值。在第4步至第13步的循环中对当前约束C中所有的解集进行处理：若解τ被证明为可行的（第7 步isValidtuple（ ）），则第 9 步、第 10 步记录τ中所有的赋值；若τ不可行，则将τ移至表的底层并修改current index与search level的数据。当该循环结束后，约束中所有的解集都进行了处理，x中所有的不被支持的赋值都被剪枝移除。 此时Unsupport=dom/gacValue。

第17 步对CSP 中削减后新的值域进行了更新，并18 步检查x的新值域是否为空。若x的值域为空，则算法返回不一致标志；若x的值域不为空，返回新的值域并可用于进一步的约束处理。

算法中第1步、第4步以及第15步中循环的时间复杂度分别为O(r')，O(r')，O(rt')，O(r'd)，其中r'=|scp/past|代表了scp中未实例化的变量数目。t'代表c的元数。因此对于任意约束c，在最恶劣情况下算法的时间复杂度为O（r'd+rt'）。

3.2 算法分析

以表2为例，算法的通用数据结构如图4所示。其中：position[i]代外延约束表中第i个可行的解集。Current index标志当前表中最后一个可行的解集。在图5 中， 当前最后的可行解为position[8]={rock2robot loc2 0right1}。

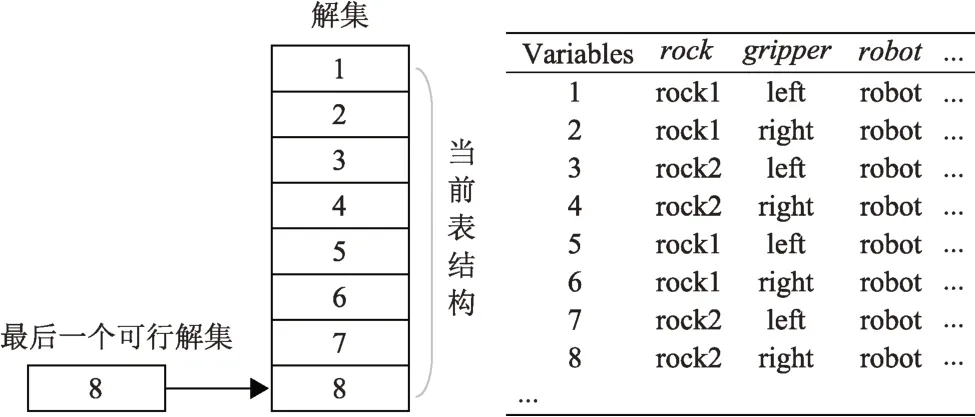
图4 外延约束快速过滤算法数据结构Fig.4 The data structure of the extensional constrained filtering algorithm

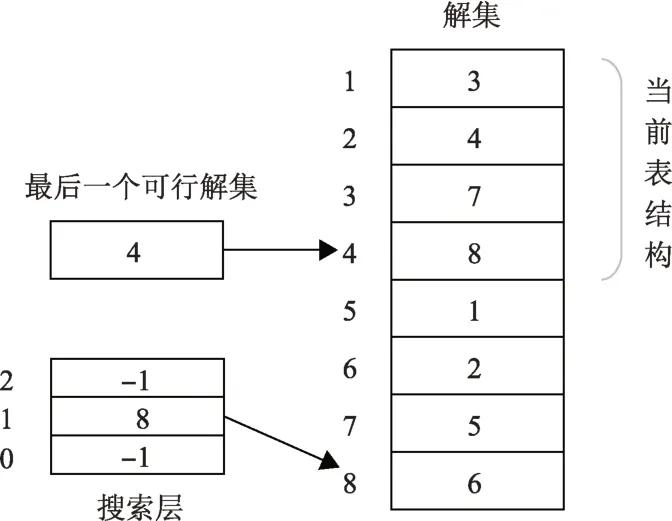
图5 外延约束快速过滤算法数据结构Fig.5 The data structure of the extensional constrained filtering algorithm

假设在规划活动中赋值对＜rock,rock1 ＞被剪枝，则表中的赋值解{1,2,5,6}由于不再满足弧一致被移除。将无效解移至表的底端后当前表的数据结构如图6所示。

search level[i]=j记录在第i层的削减操作中，约束表中第j个赋值解为第一个无效解。在上面的例子中，在第0层没有进行削减操作，因此search level[0]记为-1；在第1 次削减操作中第1 个无效解记录在约束表的第8 层，因此search level[1]= 8。若再次进行约束削减，例如移除无效赋值对＜gripper,left＞，则表的数据结构如图7所示。

在算法控制过程中对约束表中有效解/无效解进行区分保存不仅有利于数据的储存与搜索，在算法回溯时也同样提供了便利。上面的例子中，当动作约束表需要分别对赋值对＜gripper,left＞，＜rock,rock1 ＞进行回溯时，仅需修改current index与search level的指针标志，即可得到图7中的结果。注意到进行算法回溯后position表中存储的数据顺序与原表中有所不同。由于表中数据在初始存储时并未采用特定顺序排序，对表中数据的搜索又采用枚举遍历的方式，数据存储顺序的改变并不会对算法的搜索产生影响。

图6 外延约束过滤算法数据结构Fig.6 The data structure of the extensional constrained filtering algorithm

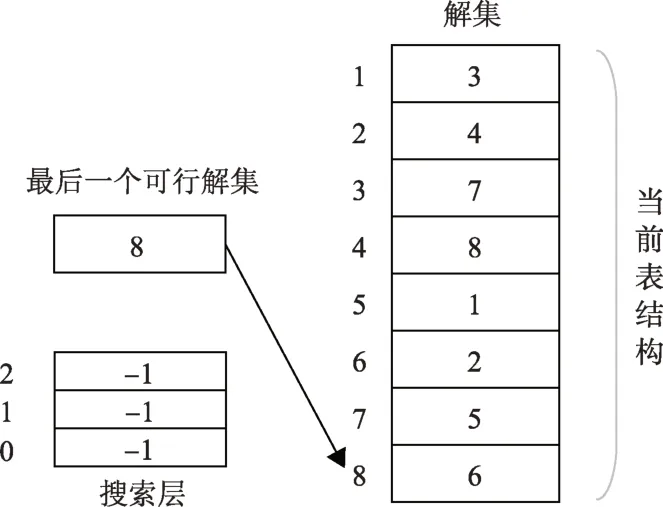
图7 外延约束过滤算法数据结构Fig.7 The data structure of the extensional constrained filtering algorithm

4 仿真实验

为了验证本文提出的过滤算法对整体规划效率的影响，仿真实验环节采用CSP 中常用的一般弧一致（General Arc Consistency，GAC）算法[16]与基于动态约束集的外延约束快速过滤算法（后文简称动态约束集算法）进行对比。在算法仿真实验中选取4种不同的规划任务Rover、Satellite、Driverlog、Zene，并通过计算机随机生成初始数据考察规划中处理的约束数量，在统一的前向搜索方法下搜索时间，分别对两种约束过滤方法进行比较分析。实验的环境配置为Intel Core i5-2450 CPU（2.5 GHz），4GRAM，Win7 操作系统，编程语言为C/C++语言。

图8 记录了不同任务，不同变量数下基于动态约束集的快速表过滤算法与GAC 算法在探测器规划任务中处理的约束数量。由于在约束可满足的处理过程中对于问题的削减同样会占用算法的运行时间，当削减算法设计不当时将严重影响搜索效率。对比算例中GAC 算法并没有考虑规划问题中活动层面的冲突，由图8 可以发现，GAC 算法考察了大量冗余的冲突约束，因此也对大量的冗余变量进行了值域削减处理，占用了算法大量的时间。而将约束层面的冲突降至变量层解决，部分变量在不同约束的限制下被过度削减到值域为空，导致算法产生回溯。而本文提出的快速过滤外延约束算法在对约束的预处理过程中根据规划的领域信息将约束分类，减少了需要处理的约束数量，由图8 中可以发现，在对于不同变量数的问题规模时，处理的约束数均少于GAC 算法。

图8 处理约束数对比Fig.8 Comparison of processing constraints

表3～6记录了上述4个算例在约束求解中分别产生的规划时间对比。从计算结果可以发现，在相同搜索算法框架下，由于快速外延约束过滤方法产生更好的过滤效果，从而降低了搜索时变量的处理规模，减少了搜索用时。同时，由于快速外延约束过滤方法需要提取规划问题中的领域信息引导削减过程，随着问题规模的增加快速外延约束过滤方法能够更加便利地利用领域信息，提高规划效率。

为了直观比较过滤算法对成功率的影响，对固定数量变量，在初值变化的情况下通过50 次实验统计进行对比。深空探测器在任务规划与调度过程中，由于约束网络通常会出现较多的变量，因此选择了变量的数量为100进行实验，统计结果如表7所示。

根据统计数据可知，在前向搜索算法框架以及变量数量为100的前提条件下，基于动态约束集的外延约束快速过滤算法的规划成功率较GAC 算法有了进一步的提升。因此在具有大量变量的约束规划模型中，快速表过滤算法更能够稳定地获得规划解，更适用于复杂的深空探测器系统。

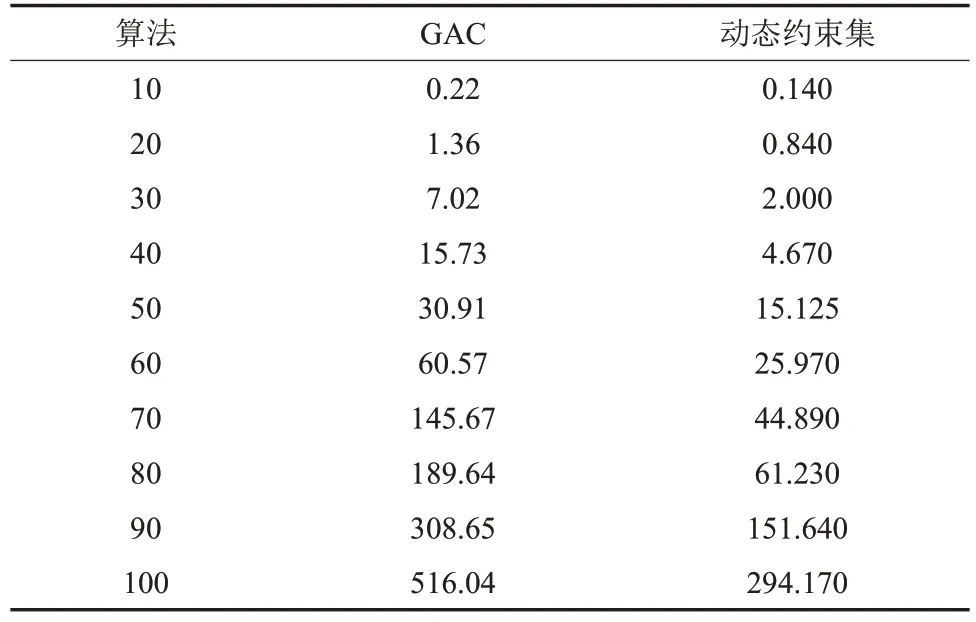
表3 算例1规划时间对比Table 3 Planning time comparison of example 1 s

表4 算例2规划时间对比Table 4 Planning time comparison of example 2 s

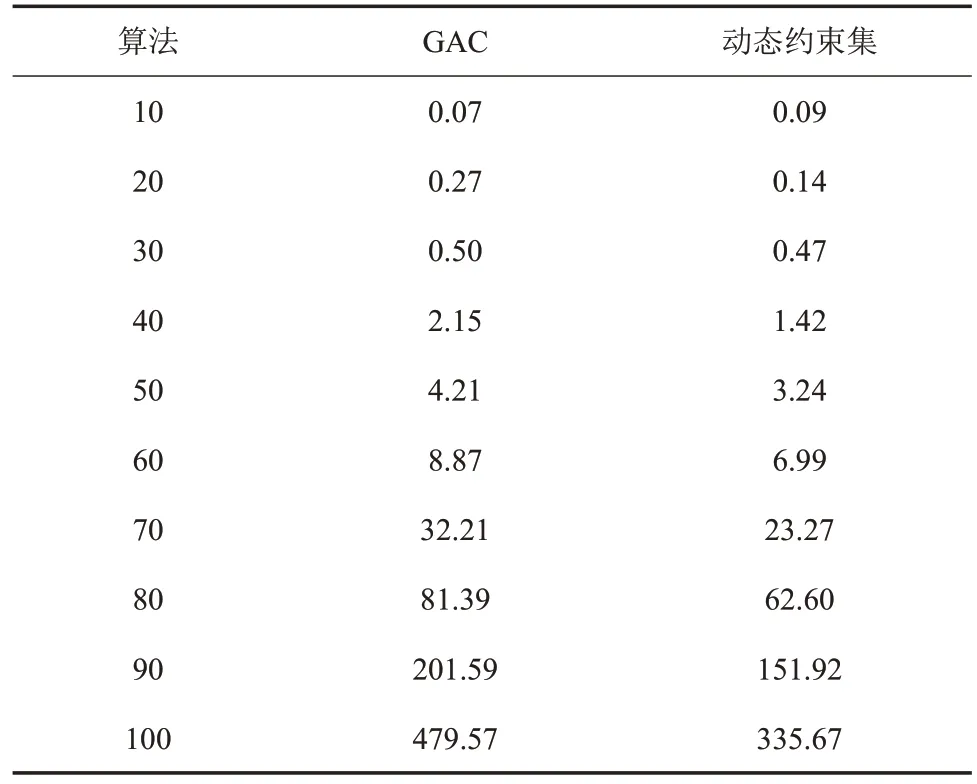
表5 算例3规划时间对比Table 5 Planning time comparison of example 3 s

表6 算例4规划时间对比Table 6 Planning time comparison of example 4 s

表7 深空探测器任务规划与调度成功率对比Table 7 Comparison of mission planning and scheduling success rate

结合对比结果，表8进一步对比不同方法生成的解的质量，评价标准包括完成任务所需时间以及规划中的空闲时间。通过对比分析可以直观地反应不同规划解安排规划活动的紧密程度。在不同算例的对比中，本文提出的动态约束集算法具有较好的任务完成时间与最小的空闲时间，表明在规划解中规划活动安排较为紧密，在相同规划周期中能够完成更多的规划任务。

表8 解质量对比Table 8 Quality comparison of different methods s

5 结 论

本文在分析深空探测器约束规划模型特点的基础上，提出了一种分层变量的动态约束集构建方法，并设计了外延约束过滤算法。该算法对活动外延约束进行分析，根据领域信息中活动间的冲突性判定对新加入的活动进行分类，从而形成一致性的约束集合。

对于约束表中变量一致性检查，设计了快速表过滤算法，通过对变量的聚类管理，能够有效地提高一致性检查以及问题回溯的效率。最后的算法仿真实验表明相较于GAC 算法，基于动态约束集的快速过滤算法能够有效地降低约束处理中无效的约束检查数目，降低问题处理过程中的回溯次数。