“火卫1”轨道预报与动力学分析

高梧桐，谢 攀，鄢建国

（1.武汉大学测绘学院，武汉，430070；2.上海卫星工程研究所，上海，201100；3.武汉大学测绘遥感信息工程国家重点实验室，武汉 430070）

引 言

“火卫1”是火星两颗自然卫星中质量较大的一颗，自1877年被发现以来，人们对“火卫1”进行了许多研究建模与观测。现有资料表明[1]，“火卫1”质量为1.0659× 1016kg，平均半径为11 km。轨道周期约为0.318 9 个地球日，平均轨道速度达2.138 km/s。近年来火星及其卫星的探测成为各国航天任务的热点。2003年，欧洲航天局（European Space Agency，ESA）发射的“火星快车”（Mars EXpress，MEX）进行了飞越“火卫1”探测并收集了大量有价值的数据[2]。我国首次独立自主的火星探测任务将于2020年进行，任务期间有可能开展“火卫1”飞掠测量。日本宇宙航空研究开发机构（Japan Aerospace Exploration Agency，JAXA）也已经确定火卫探测任务及“火卫1”采样返回计划MMX（Martian Moons eXploration）[3]。更长远来说，美国国家航空航天局（National Aeronautics and Space Agency，NASA）计划在21世纪30年代将人类送往火星[4]。探究“火卫1”的轨道，对于未来的火星探测有着重要意义。

由于“火卫1”轨道的重要性，国际上多个机构开展了这方面的研究。目前“火卫1”历表可以从由喷气动力实验室（Jet Propulsion Laboratory，JPL）的火星卫星星历MAR097、俄罗斯的EPM2017 和法国的INPOP17a 获取。MAR097 星历是JPL 发表的火星卫星星历[5]，通过对火星卫星的数值积分，使用地球观测数据和探测器影像观测数据进行拟合。该星历的动力学模型中主要为火星重力场模型MGS95J[6]（包括8 阶带协项与5 阶次田协项），“火卫1”和“火卫2”的互相影响，太阳、地月系统、木星和土星的摄动，“火卫1”的天平动，“火卫1”引起的火星潮汐。但由于计算软件限制，并未使用重力场模型MGS95J对应的火星自转模型，而是使用了对应的ICRF（International Terrestrial Reference Frame）参考框架，计算过程中通过星历DE421 获取太阳、行星及其卫星的位置和常数。

EPM（Ephemeris of Planets and the Moon）是俄罗斯科学院应用天文学研究所（Institute of Applied Astronomy of the Russian Academy of Sciences，IAARAS）发表的一套高精度星历数据集[7]，目前EPM最新版本为EPM2017及其加长版本EPM2017H，包括太阳及其行星（包括冥王星）、各行星卫星、小行星等星历数据，涵盖时段分别为1787-2214 和10107BC-AD3036。 EPM2017 （H）参考系选取ICRF2，定向精度高于0.2 mas，时间系统选取质心动力学时（Barycentric Dynamical Time，TDB），在动力学模型方面，引入了太阳扁率、301 颗大型小行星、30 颗大型外海王星天体，小行星带、柯伊伯带等摄动影响。行星星历部分，共解算了约270 个参数。通过IAARAS 官网的星历计算服务[8]，选择EPM2017星历，可以计算“火卫1”的星历。

INPOP17a 是由法国天体力学与星历计算研究所（Institute of Mechanics Celestial and Calculation of Ephemeris，IMCCE）发表的行星及卫星星历[9]，它提供各大天体在ICRF（International Terrestrial Reference Frame）坐标框架下轨道数据和TT-TDB 时间转换参数。INPOP17a 在火星星历部分拟合了当时最新的MEX、Mars Odyssey 探测器的观测值信息，并在动力模型上引入了168颗小行星的摄动影响。与EPM一样，通过IMCCE 官网计算服务[10]，以INPOP17a为行星星历，可以获取“火卫1”的星历数据。

本文结合最新的“火卫1”摄动力模型，通过高精度数值积分方法计算“火卫1”的轨道，并将计算结果与多个历表进行验证，确保模型的精度和可靠性。通过这一工作，可以分析不同的摄动力源对“火卫1”轨道的影响，将对后续“火卫1”探测任务的开展提供参考。

1 积分器及动力学模型

本文主要通过对“火卫1”运动方程进行数值积分来实现对“火卫1”的轨道预报。积分过程中初始状态向量从现有星历中获取，方法采用精度较高的Rouge-Kutta-7(8)积分器[11]进行起步，然后使用计算性能较好的Adams-Bashforth-Moulton 积分器[12]进行后续积分。

经对“火卫1”的受力分析可知，中心天体火星的引力是“火卫1”受力的主要来源，计算过程中首先考虑了最基本的质点模型，但是火星内部质量分布并不均匀，形状也不规则，考虑非球形摄动，将扰动位函数进行球谐展开，得到[13]

其中：Re为火星的半径；为完全正规化的二阶勒让德函数；r、ψ、λ为“火卫1”在火星固定坐标框架下的3个球坐标分量；为完全正规化后的重力场模型球谐系数。

对于中心天体以外的天体，其“火卫1”的引力摄动用质点模型表示。引入了潮汐模型，考虑火星的二阶固体潮Love 数，对于某一质量为Mj、半径为ae的摄动天体，在火星上产生固体潮，对“火卫1”的引力位函数为[14]

其中：r为“火卫1”相对火星的距离；rj为“火卫1”相对摄动天体的距离。

另外，若视“火卫1”运行轨道为圆轨道，某一质量为Mj的天体，受广义相对论效应的影响，对卫星的引力加速度产生相应的修正[15]为

相对论效应修正量等于该天体对“火卫1”的引力加速度与3v2/c2的乘积，对于一般的卫星，3v2/c2约为3× 10-10，考虑足够长时间时，相对论效应引起的误差不容忽视。

该算法参考时间系统为以太阳系质心为中心的TDB 时间系统，起始时刻为J2000.0（2000－01－01 12:00:00）。参考框架选取火星惯性系J2000，计算火星重力场过程中涉及到的火星固定坐标系，由对应的重力场模型中给出的火星自转模型求得。摄动天体的位置通过行星星历DE430[16]获得。火星和“火卫1”的质量和半径从对应重力场模型获取。此外，其它天体的质量、半径等常数，UTC 到TDB 时间转换过程中的闰秒数据，以及用于对比的“火卫1”的星历也从对应的SPICE Kernel 文件读取，这些数据均可在NASA的NAIF机构官网[17]获得。

2 动力学模型影响分析

对“火卫1”轨道计算时，所引入的动力模型越完善，计算效果越好，但同时计算时间成本和空间成本随之增大。数值积分时，既要尽可能保证力模型的全面性，又要考虑计算性能和效率。本节在考虑某项动力学模型和不考虑该模型的情况下，在一段时间内计算各自的轨道位置，由3 个位置分量的差异dx、dy、dz，计算位置差异dr，分析其影响量级，进而考虑是否引入该模型。

2.1 重力场阶数

随着采用重力场模型阶数的增大，轨道预报结果精度将会提高。但是对于每一步积分求值，重力场模型计算的时间复杂度是O(n2)，其中n为重力场阶数。应合理选择重力场模型的阶数，在合理的精度下，控制计算的时间成本。计算过程中选取重力场模型MRO120D 及其对应的火星自转模型[18]进行重力场的计算，最高阶数计算到20 阶，后续阶次的增大对计算结果没有影响。火星引力常数为42 828.375 815 756 1 km3/s2，参考半径为3 396 km。为确保中心引力模型的一致性，算法同时适配了一阶重力场模型，即将中心天体视为质点的重力模型，同时比较了引入重力场模型与质点模型对计算结果影响的量级。试验过程中随机选取1982－1992 和2000－2010 两个时间段，在不同阶数重力场模型下计算轨道结果，并与MAR097星历比较，计算不同阶数10年最大距离误差dr，结果如图1 所示。

图1 不同阶数MRO120D重力场模型引起的最大轨道误差Fig.1 Max distance difference caused by MRO120D gravity field model in different degrees

两个时间段的比较结果具有一致性，均说明1阶重力场模型（质点引力模型）能够对“火卫1”产生数千千米的轨道偏差，因此实际计算过程中不能简单将火星视为质点。在重力场模型6阶以后距离误差的量级便稳定下来，10 阶以后重力场计算结果的差异仅在几米到十几米。考虑计算成本，重力场模型阶数选择6～10阶即可。

2.2 N体摄动

本节比较了太阳及除火星以外各天体系统的摄动对“火卫1”轨道的影响，比较时段为10年。首先在两次积分过程中，分别引入和不引入太阳的引力摄动，比较太阳摄动对“火卫1”位置的影响，结果如图2所示。

可以看到，在10年这一长周期的积分时段内，太阳摄动引起的“火卫1”轨道差异最高可达30 km，并随时间呈线性增长。曲线放大后，可以发现存在振幅为数千米的高频振荡。因此可以得到结论，太阳摄动无论在10年的长周期，还是在较短的时间段内，都会对“火卫1”的轨道产生不可忽略的影响。

图2 太阳摄动引起的轨道误差Fig.2 Distance difference with and without considering perturbation of Sun

按照相同的思路，对太阳系各行星系统（包括其卫星）摄动对“火卫1”轨道的影响进行分析，需要注意的是，各行星系统的位置矢量指向的是对应的行星系统质心，而非单个行星的质心，质量也应考虑行星与卫星的质量总和。对各行星系统的引力摄动影响分析结果如图3所示。结果表明，在10年的时间尺度计算“火卫1”轨道，行星系统引力摄动引起的轨道差异量级仅在几米到十几米不等，大多数摄动天体的作用可以忽略。而太阳摄动引起的距离差异能够占所有三体摄动的99%以上，因此，计算过程中必须要考虑太阳的摄动。对于其它天体摄动，在长时间段内引起的距离误差量级都是可以忽略的，是否引入可以依照差异量级的大小和考虑摄动模型的完善性进行选择。

图3 太阳系及其他行星系统摄动引起的轨道误差Fig.3 Distance difference of other planets in solar system

2.3 潮汐摄动

对于每一个天体引起的潮汐模型的分析，与N体摄动分析方法一致。由于太阳与“火卫1”是火星固体潮汐摄动的主要来源[19]，因此在潮汐模型中不再引入其余天体。在考虑火星二阶“Love 数”的情况下，太阳和“火卫1”使得火星固体部分产生弹性形变，进而改变了火星的质量和重力场分布，最终对“火卫1”轨道产生的影响如图4 所示。由图4 可知，太阳和“火卫1”固体潮汐在10年的时间段对“火卫1”位置的影响最大分别为300 m和75 m左右，要大于行星系统的摄动引力影响。从误差大小来看，可以在保证计算效率的前提下引入太阳和“火卫1”的潮汐影响。

2.4 相对论效应

一般来说，天体相对论效应产生的对卫星的引力修正项的大小取决于天体的施瓦西半径（2GM/c²）和卫星的速度。所以，与N体摄动、潮汐摄动一样，所有对“火卫1”产生相对论效应的天体中，太阳占主导作用。太阳引起的相对论效应对“火卫1”轨道的影响结果见图5。在短时间内相对论效应引起的误差量级可以忽略，但是对于10年的积分间隔，相对论效应将会对“火卫1”轨道产生最大5 km 的影响，误差随时间大致线性增长。综上所述，最终的轨道预报模型，采用的动力模型及参数如表1所示。

图4 太阳和“火卫1”潮汐引起的轨道误差Fig.4 Distance difference caused by tidal effect of Sun and Phobos

图5 太阳相对论效应引起的轨道误差Fig.5 Distance difference caused by relativity effect of Sun

表1 “火卫1”轨道预报采用的动力模型及参数Table 1 Force models and parameters in orbit prediction of Phobos

3 星历对比

本节将计算出的“火卫1”轨道与3 种星历进行差异比较，分别选取JPL 的MAR097 火星卫星星历，以及由俄罗斯EMP2017 和法国INPOP17a 求得的“火卫1”星历。比较过程中，首先由从各自星历中获取初始状态向量，分别计算轨道数据，并与对应星历相比较，计算距离差。其次，将状态向量转换为轨道根数（半长轴SA、离心率E、轨道倾角I、升交点赤经RAAN、近地点角距AOP 和平近点角MA），再分别做差比较。利用上述的动力模型及积分器，设定初始时间为1982－03－26 UTC，从3 种星历中获取的初始状态向量如表2所示。

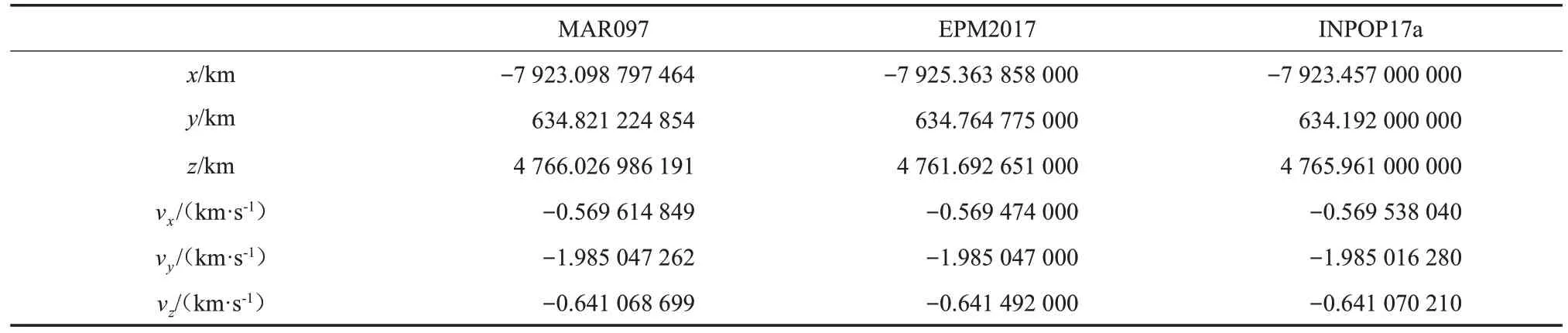
表2 “火卫1”1982-03-26 UTC时刻下在3种星历中的状态向量Table 2 State Vectors of Phobos in three different ephemeris at 1982-03-26 UTC

与MAR097 星历比较时，首先取一年的积分时长，比较短期内的距离误差与轨道根数误差，评价该算法模型的精度（结果见图6 和图7）；再取10年的积分时长，验证模型的稳定性（结果见图8 和图9）。按照同样的方法，分别比较其轨道距离差异和轨道根数差异，对“火卫1”轨道预报模型进行进一步验证（结果分别见图10～11和图12～13）。

图6 与图7 的结果表明，该模型在1年内的轨道计算结果与MAR097 星历相比，最大距离差异为900 m 左右，误差图像高频振幅也随时间缓慢增长，而轨道长半轴的差异不超过±0.25 m，其余轨道根数的差异量级也足够微小。将散点放大后可以发现，轨道倾角、升交点赤经两个轨道根数中，高频部分相对的振幅较小且随时间变化不大，而长半轴、离心率、近地点角距和平近点角的误差图像的振幅随时间线性增长。

图6 与MAR097相比1年轨道距离误差Fig.6 Distance difference in 1 year compare with MAR097

图7 与MAR097相比1年轨道根数误差Fig.7 Orbital difference in 1 year compare with MAR09

通过图8 和图9 可知，将比较时段拓展到10年，最终距离误差与一年的结果相比，误差增长趋势基本一致，图像振幅逐渐减小，最大距离差异为8 km 左右。10年的轨道根数差异中，轨道倾角和升交点赤经差异开始呈现出周期性变化趋势，差异都大致收敛在±10-5量级内，而长半轴、离心率、近地点角距和平近点角在误差图像的增长趋势上与1年的比较结果相一致，仅在数值上相比有一个量级的增加。

图8 与MAR097相比10年轨道距离误差Fig.8 Distance difference in 10 years compare with MAR097

图9 与MAR097相比10年轨道距离误差Fig.9 Orbital difference in 1 year compare with MAR097

图10 与图11 为模型计算结果与星历EPM2017在10年内的比较结果，与MAR09710年的比较结果有所不同的是，计算结果与EPM2017 的轨道距离误差幅度变化较大，一年内差异达到了5 km，但是基本不随时间增长，逐渐收敛。轨道根数中，近地点角距的误差图像呈现出周期性变化的趋势，图像中高频振幅逐渐增大，与MAR097 对应的图像存在差异。从数值上来看，长半轴、离心率、近地点角距和平近点角的差异与MAR09710年轨道根数比较结果相似，都在同一量级，但是升交点赤经和轨道倾角的差异增大了两个量级。

图10 与EPM2017相比10年轨道距离误差Fig.10 Distance difference in 10 years compare with EPM2017

图11 与EPM2017相比10年轨道距离误差Fig.11 Orbital difference in 1 year compare with EPM2017

图12与图13为模型与星历 INPOP17a 在 10年内的比较结果，其无论是轨道距离差异还是轨道根数差异都与MAR097的比较结果相似，差异也都随时间大致呈线性增长。其根本原因是MAR097 中“火卫1”星历信息与INPOP17a 求得的“火卫1”星历互相差异本身就十分小，在10年内不到2 km，而且误差也不随时间增长，呈收敛趋势。

可以看到，该数值模型得到的“火卫1”轨道预报结果与MAR097、EPM2017 与INPOP17a 三种星历对比，10年内距离误差在10 km 以内。对比分析可知，计算结果对JPL 星历MAR097 的拟合效果最好，误差最小。主要原因是在动力学模型计算过程中涉及到的各天体的位置信息都从JPL 星历DE430 中获取。若要进一步对星历EPM2017 和INPOP17a 进行拟合，可以改为从其各自对应历表获取其他天体位置信息。

图12 与INPOP17a相比10年轨道距离误差Fig.12 Distance difference in 10 years compare with INPOP17a

图13 与INPOP17a相比10年轨道距离误差Fig.13 Orbital difference in 1 year compare with INPOP17a

为了比较模型计算结果的精度，图14 比较了以上3 种星历各自之间在10年相同计算时段下“火卫1”轨道的位置差异，可以看到，不同星历之间1年内便出现了数千米的距离差异。但由于这些星历都使用了实测数据对“火卫1”进行精密定轨，所以其相互间的差异不会随时间增长，并且在观测数据密集的时间段误差相对较小。从数值上来看，差异最大的是EPM2017 与INPOP17a，最大值6 km，最小值的是MAR097 与INPOP17a，仅为1.6 km。这是因为INPOP 系列星历本身就与JPL 的DE 系列星历在观测资料方面体现出较好的一致性，所以计算出来的火卫一星历与MAR097 相差较小。而EPM2017 与其他两者差异较大，这可能是观测值数据处理和加权方案的不同引起的。

在未引入观测值的条件下，该轨道预报模型的计算结果，在不同时段与不同来源的星历比较后体现出的差异，和星历自身之间的差异性相比，量级一致，仅在数值上稍大。可以充分说明该模型的预报结果在短期具有足够的精度，长期也有一定的可靠性。

图14 星历MAR097，EPM2017和INPOP17a之间的“火卫1”轨道距离差异Fig.14 Distance difference between MAR097，EPM2017 and INPOP17a

4 结 论

本文通过对“火卫1”的动力学影响分析，确定了数值积分计算“火卫1”轨道的动力模型，最终与不同星历进行了比较分析。可以得到结论，该算法模型计算和预报“火卫1”的轨道是切实有效、可靠的。实验结果也存在需要改进的地方。从长时段的星历比较结果来看，只利用动力模型计算出的数值结果和真实星历存在10 km左右的差异，其中重要的原因是数值积分本身的误差累计。真实星历在数值积分的同时使用了许多对“火卫1”的观测值信息，对卫星轨道进行改正，有更良好、稳定的精度[20]。在动力模型部分，后续考虑“火卫1”的天平动有望取得更好的计算结果[21]。

“火卫1”的轨道预报，可用于研究其轨道的性质及其随时间的变化。接下来的工作将以此为基础，结合对“火卫1”的观测信息，特别是火星快车飞掠期间观测的大量针对“火卫1”的影像数据，建立高精度的星历。现有的火卫历表尚未处理这一数据。联合“火星快车”地面深空站数据、“火星快车”对“火卫1”的影像数据、地基“火卫1”影像数据，进行“火星快车”和“火卫1”联合定轨，有望进一步改进“火卫1”的轨道精度，进而在未来的“火卫1”探测任务中发挥重要的作用。