火星车双向抽展式转移坡道展开原理及特性分析
马 超,刘 卫,满剑锋,刘 飞,潘秋月,陈 明,姜生元
(1.哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨 150080;2.北京空间飞行器总体设计部,北京 100094)
引 言
火星是太阳系八大行星之一,是太阳系中各方面条件与地球最为相似的行星。火星上是否有水源,火星是否有生命的存在,人类能够移民火星吗?长期以来,火星对人类有着特殊的吸引力。美国国家航空航天局(National Aeronautics and Space Administration,NASA)、欧洲航天局(European Space Agency,ESA)和印度空间研究组织(Indian Space Research Organization,ISRO)都已成功向火星发送了探测器甚至是登陆车,目前已有超过30 枚探测器到达过火星,并向地球发回了大量的数据[1-6]。火星成为除地球以外,人类了解最多的行星。受天体运行规律的约束,每26个月才有1次火星探测有利发射时机,2020年前后,有4次火星探测任务发射,将在国际上将迎来火星探测的高峰[7-8]。
中国首次火星探测任务将于2020年左右实施,一步实现“绕”“着”“巡”的目标。着陆器在火星表面软着陆时存在诸多得不确定性,是任务的重大难点之一[9]。火星车着陆火星表面后,需要从着陆平台通过坡道机构转移至火星表面。由于着陆局部区域地形地貌的随机性[10],要想实现火星车的安全转移,对坡道机构提出了转移平缓、适应地貌、轻量化等方面苛刻要求,坡道长度将超过着陆平台包络尺寸的1.5倍。转移坡道的紧凑布置、驱动共用、可靠展开等问题,成为火星车转移坡道设计的关键[11]。
1 双向抽展式转移坡道
根据我国火星车性能指标及对预定着陆区域的预估,要求在最极端的着陆工况下(地面坡度± 15°,着陆平台姿态倾角±6°,地面凸起或凹坑≤200 mm)坡道所提供的最大转移坡道角≯30°,经过计算坡道长度应≥4 860 mm,受着陆平台包络直径3 000 mm的限制,坡道在着陆平台安装方式需要采用折叠或两折重叠布置[12],本文提出一种双向抽展式转移坡道,安装在火星车两侧车轮的正下方,单侧坡道由根/末梯组件组成且左右重叠布置,与着陆平台之间通过导向辅道组件提供直线导轨约束。当着陆器软着陆后,动力绳轮组件中的卷筒开始回转,驱动两侧坡道按照先外梯后内梯的顺序直线展开,展开到位后摆转触地,等待火星车转移,坡道初始状态如图1所示,展开状态如图2所示。
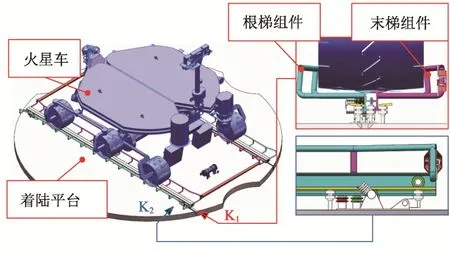
图1 双向抽展坡道初始状态示意图Fig.1 Schematic diagram of the initial state of the two-way
2 抽展原理分析
2.1 抽展动作流程
双向抽展式转移坡道方案,基本动作工作流程如图3所示。
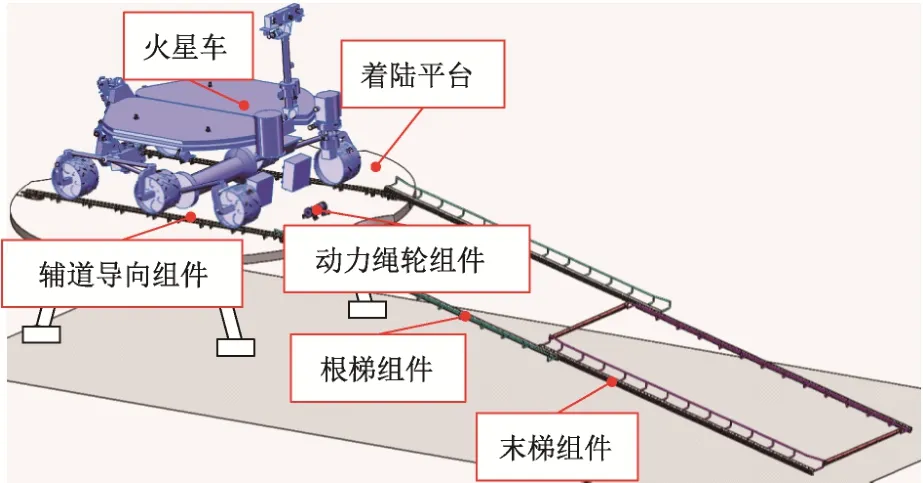
图2 双向抽展坡道展开状态示意图Fig.2 Schematic diagram of the unfolding of the two-way ramp
2.2 绳轮抽展原理
根据航天轻量化、低功耗、电接口数量尽量少等设计原则,确定了单电机卷筒同时拖动两侧坡道抽展。为满足双向可选抽展的要求,绳轮系统布局及抽展原理如图4所示。
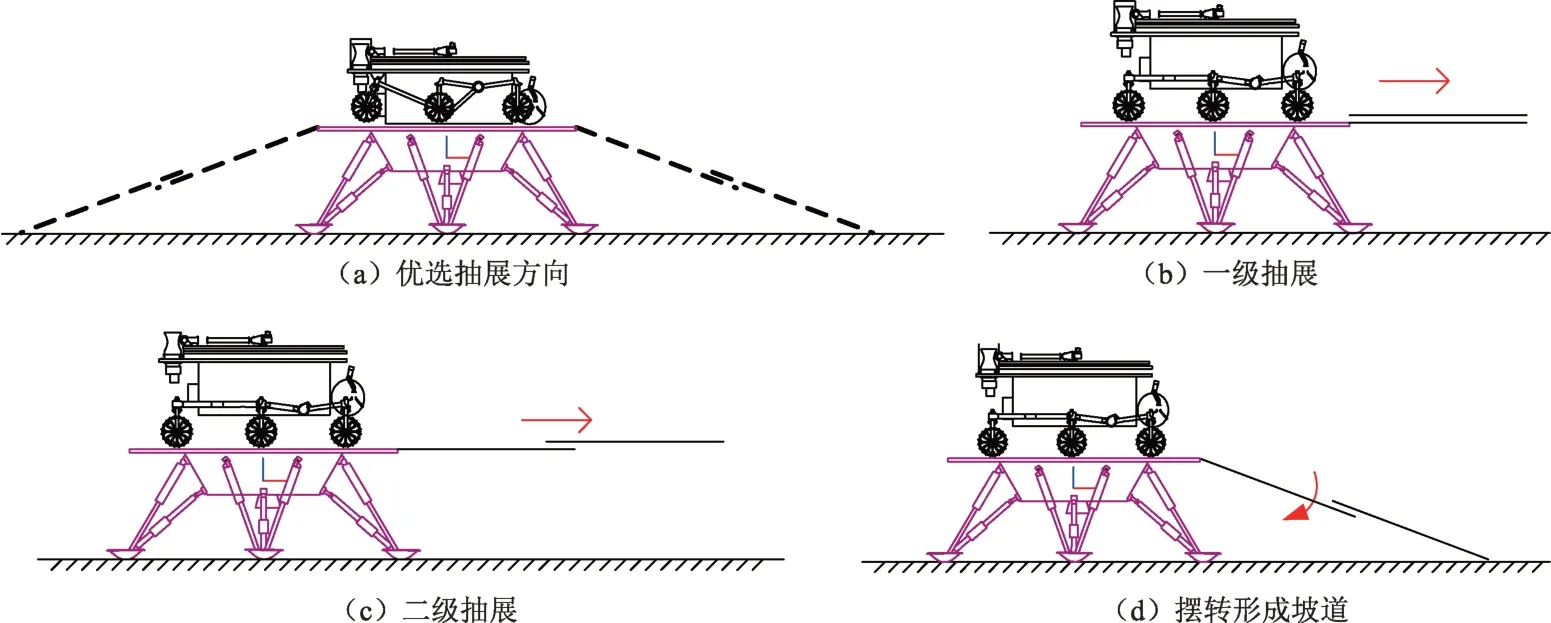
图3 双向抽展式转移坡道方案动作流程图Fig.3 Flow chart of two-way draw-out transfer ramp scheme

图4 单侧坡道绳驱抽展原理Fig.4 Principle of single-sided ramp rope drive
3 坡道展开特性分析
根据电控式双层抽展坡道方案工作原理及动作流程,建立坡道展开过程力学模型,依次分析坡道处于不同展开姿态时系统负载的变化趋势,为后续系统组件的详细设计提供参考依据。
3.1 电控双层抽展坡道简图与力学参数释义
由于展开坡道属于沿Z向对称结构,因此进行展开过程受力分析时,可将系统结构简化成如图5所示的单侧坡道力学模型。
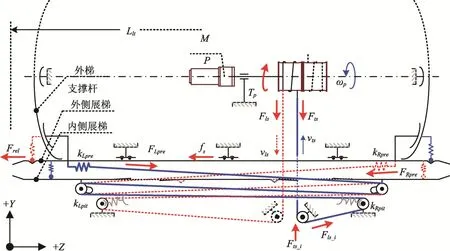
图5 电控双层抽展坡道受力分析图Fig.5 Stress analysis diagram of electronically controlled double-layer pumping ramp
根据双层抽展结构可知,伺服电机通过驱动缠绕在卷筒上的绳索抽展位于着陆平台两侧的坡道组件,抽拉绳索末端分别与外侧末梯两端通过弹簧kpre相连,以提供抽拉预紧力Fpre。图5 中假定坡道的优选展开方向为+Z向(右向),驱动电机MP以转速ωP沿+Z向逆时针旋转(遵循右手定则),蓝色粗线表示电机抽拉绳索、红色虚线表示送拉绳索。
末梯在收拢状态下由两根末梯支撑杆通过力控锁销连接双侧坡道,在选择展开方向(+Z向)后,电机需先通过绳索驱动末梯脱离左侧末梯支撑杆锁合力Frel,在随后的双侧末梯共同抽展过程中,末梯仅需克服其自身与导向辅道间的摩擦力fs。抽拉绳索在与末梯相连时需通过若干滑轮组导向,经过第i个滑轮前后的负载分别为紧边拉力Fts_i、松边拉力Fls_i。通过卷筒两端的绳索拉力分别为紧边拉力Fts、松边拉力Fls,卷筒驱动负载为Tp。
3.2 电控双层抽展坡道展开过程受力分析
由电控式双层抽展坡道展开流程知,电机驱动卷筒缠绕抽拉绳索依次实现一级抽展、二级抽展以及末梯俯仰3个过程,系统在3个过程中的受力分析分别如图6~8所示。
在一级抽展过程中,电机的驱动负载主要来自抽拉绳索与导向滑轮间摩擦力以及内/外坡道与导向辅道间的摩擦力。在二级抽展过程中,电机的驱动负载由内/外坡道与导向辅道间的摩擦力改变为内、外坡道之间的摩擦负载。当末梯开始做俯仰展开时,电机需要克服俯仰展开铰链kRpit反力。为了确保各动作环节依次进行,需要保证展开铰链提供最大负载,因此将第3种展开状态作为分析电机负载的极限条件进行力学分析。

图6 一级抽展过程受力分析图Fig.6 Stress analysis diagram of the first stage drawing process
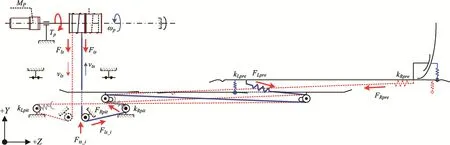
图7 二级抽展过程受力分析图Fig.7 Stress analysis of the secondary pumping process

图8 坡道摆转过程受力分析图Fig.8 Stress analysis of the slope swing process
电控绳轮组件如图9所示,主要由电机减速器组件、驱动卷筒、抽拉绳索、导向滑轮以及预紧弹簧组成,在计算系统负载前需要针对各组成部分依次开展单元力学建模。
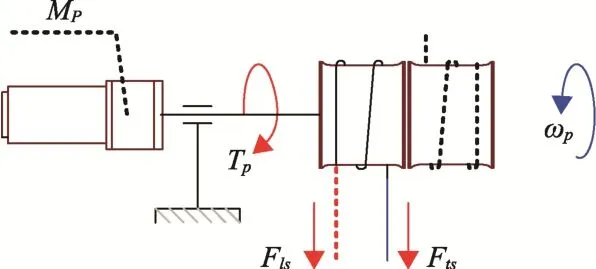
图9 伺服电机驱动卷筒组件受力分析图Fig.9 Force analysis diagram of servo motor driven reel assembly
假设电机输出轴匀速转动,整个驱动过程时刻处于准静态状态,对驱动单元建立力学关系式为
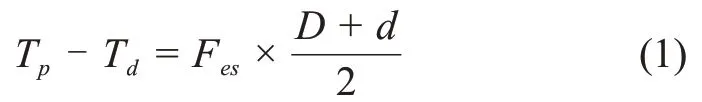
其中:Tp为电机驱动力矩;Td为轴系阻力矩;Fes为加载钢丝绳驱动力;D为卷筒直径;d为钢丝绳直径。
实际计算过程中,轴系阻力矩所带来的影响很小,此处可以作为电机转矩计算时所预留的裕度。抽拉绳索的驱动力来源于绳索与卷筒的摩擦,即绳索两端的拉力差为

其中:Fts为钢丝绳紧端拉力;Fls为钢丝绳松端拉力。
由摩擦传动中欧拉公式,可得松、紧端拉力的关系。

其中:f为卷筒与钢丝绳的摩擦系数;N为钢丝绳在卷筒上缠绕的总圈数;α0为钢丝绳在卷筒上缠绕一圈的包角;α为钢丝绳在卷筒上的包角。

图10 滑轮传动模型Fig.10 Pulley drive model
滑轮传动与摩擦传动情况类似,区别在于钢丝绳在滑轮上仅缠绕一圈,相应的也由式(3)可以求出滑轮的紧边拉力、松边拉力。
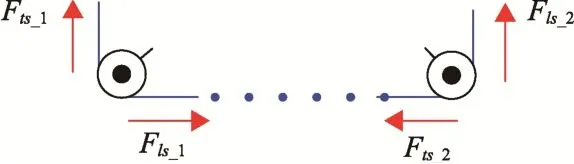
图11 滑轮传动力作用关系Fig.11 Pulley drive force relationship
对两个传动链相邻的滑轮来说,前一个滑轮的的紧边拉力等于后一个滑轮的松边拉力,以此类推拉力由卷筒驱动力一直传递到负载作用模型上。
对绳轮传动系统中,有如下关系式成立

由于抽拉绳索将依次通过5个滑轮缠绕到驱动卷筒上,因此根据欧拉公式及式(4)有

其中:各滑轮包角为α1=α2=π/2,α3=α4=α5=π。
则由式(3)和(5)可得,作用在外侧末梯上的抽拉力为
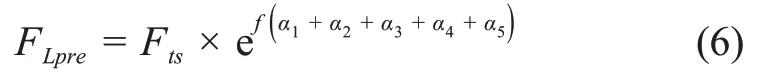
同理可得作用在外侧末梯上的松拉力为

其中,各滑轮包角为α6=α7=π/2,α8=α9=α10=π。
则将式(6)(7)及(3)代入(2)可得电机驱动力为
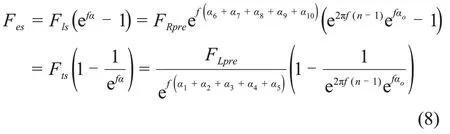
当系统处于一级抽展过程时,双梯与导向辅梯间的摩擦阻力满足关系为

则将式(6)、(7)及(9)代入(8)可得在该阶段单机驱动负载为
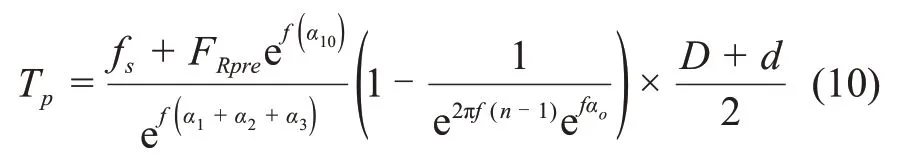
当系统处于二级抽展过程时,末梯与根梯间的摩擦阻力满足关系为
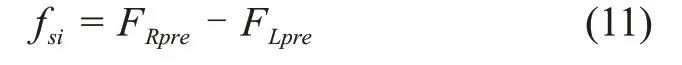
且Fts满足
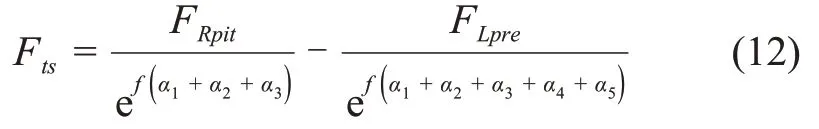
则将式(3)、(7)、(11)及(12)代入(2)可得在该阶段单机驱动负载为

当系统处于末梯俯仰过程时,俯仰铰链反力满足关系式为
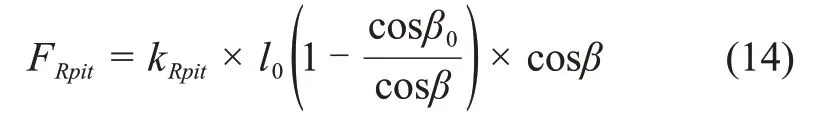
代入上式可得
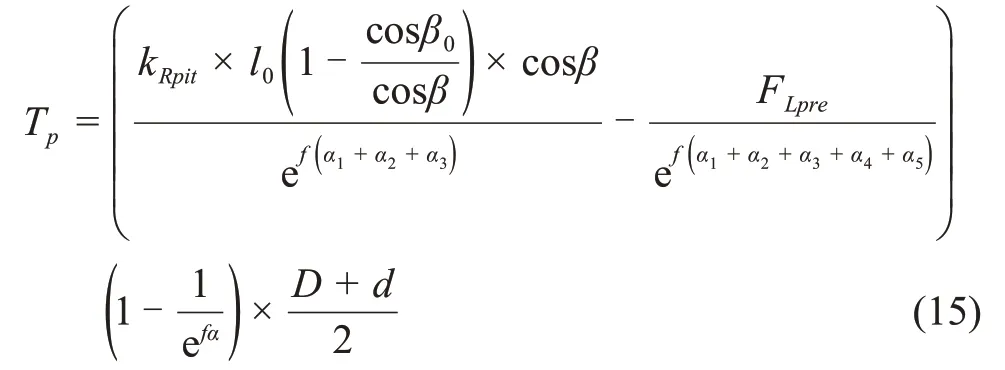
其中:l0为弹簧原长;kRpit为弹簧刚度系数;β0为弹簧初始姿态角度;β为弹簧工作状态角度。
3.3 抽展负载计算结果
通过力学模型参数式可以看出,抽展负载诸多参数都有关联。其中α、l0、β0、β、D和d可以根据空间布局、结构强度和工程经验初步确定。考虑驱动钢丝绳再抽展全程不得从滑轮和卷筒槽道脱离,可以初步给定Fls≥5 N,整个力学参数式子就有了初始条件。但是摩擦系数f和弹性系数k不可预知,跟加工制造、外购件质量以及使用环境等因素都有影响,所以需要初步确定两个变量的取值范围,利用Matlab 绘制展负载与摩擦系数和弹性系数的关系曲线如图12所示。
从图12 关系曲线可以看出,在摩擦系数取0.01~0.3,弹性系数取1~10 N/mm,可求得Fts1、Fts2和Fts3分别等于140.8 N、135.6 N和268.1 N,Tp1、Tp2和Tp3等于21.19 Nm、20.40 Nm 和40.35 Nm。得到的基本规律为Fts2<Fts1<Fts3,Tp2<Tp1<Tp3,由于抽展开始坡道接触的滑轮最多,所以比第二级抽展负载要大,最后临近摆转的时刻坡道整体外伸出平台,重力弯矩加大了对最后几个滑道的正压力所以负载最大,理论计算与实际仿真规律相符。

图12 抽展负载与摩擦系数和弹性系数的关系Fig.12 Relationship between pumping load and friction coefficient and elastic coefficient
4 抽展试验验证
4.1 火星重力模拟
火星重力环境约为地球重力的3/8,由于坡道抽展速度较低(约为634 mm/min),综合考虑试验成本和实施便捷性,采取了气球悬吊法进行火星重力环境模拟,系统方案如图13所示。
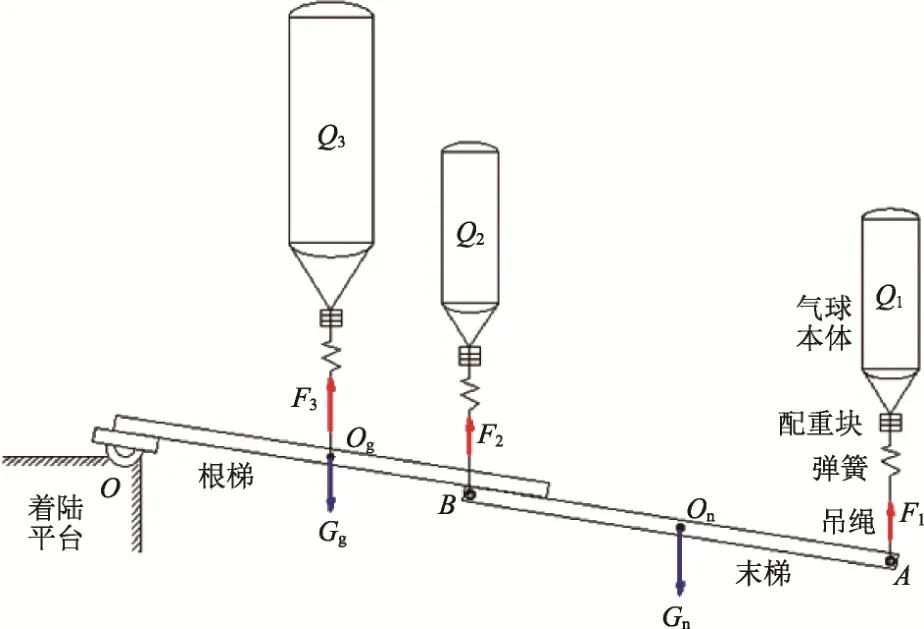
图13 3/8 g气球悬吊系统Fig.13 3/8 g balloon suspension system
对+Y和-Y侧根/末梯组件进行了实际承重,并计算出5/8 g补偿力如表1所示。

表1 根末梯5/8 g补偿力统计Table 1 statistic of the 5/8 g compensation force at the end of the ladder
4.2 测试系统搭建
为了测试坡道机构在展开过程的全程抽展阻力、摆转成道角度、抽展时间、抽展同步性、驱动效率等参数,除了产品自身的角位移传感器和行开以外,在测试平台上新增了张力计、拉线编码器、电压/电流计等传感器,具体布置位置见图14。
4.3 抽展阻力测试
在平姿和仰姿14°两种工况下,利用1 号/3 号张力计分别测试+Y/-Y侧坡道向+Z方向抽展的阻力,测试结果如表2所示。

图14 展开试验测试平台传感器布局Fig.14 The sensor layouts of the unfolds the bed-test platform
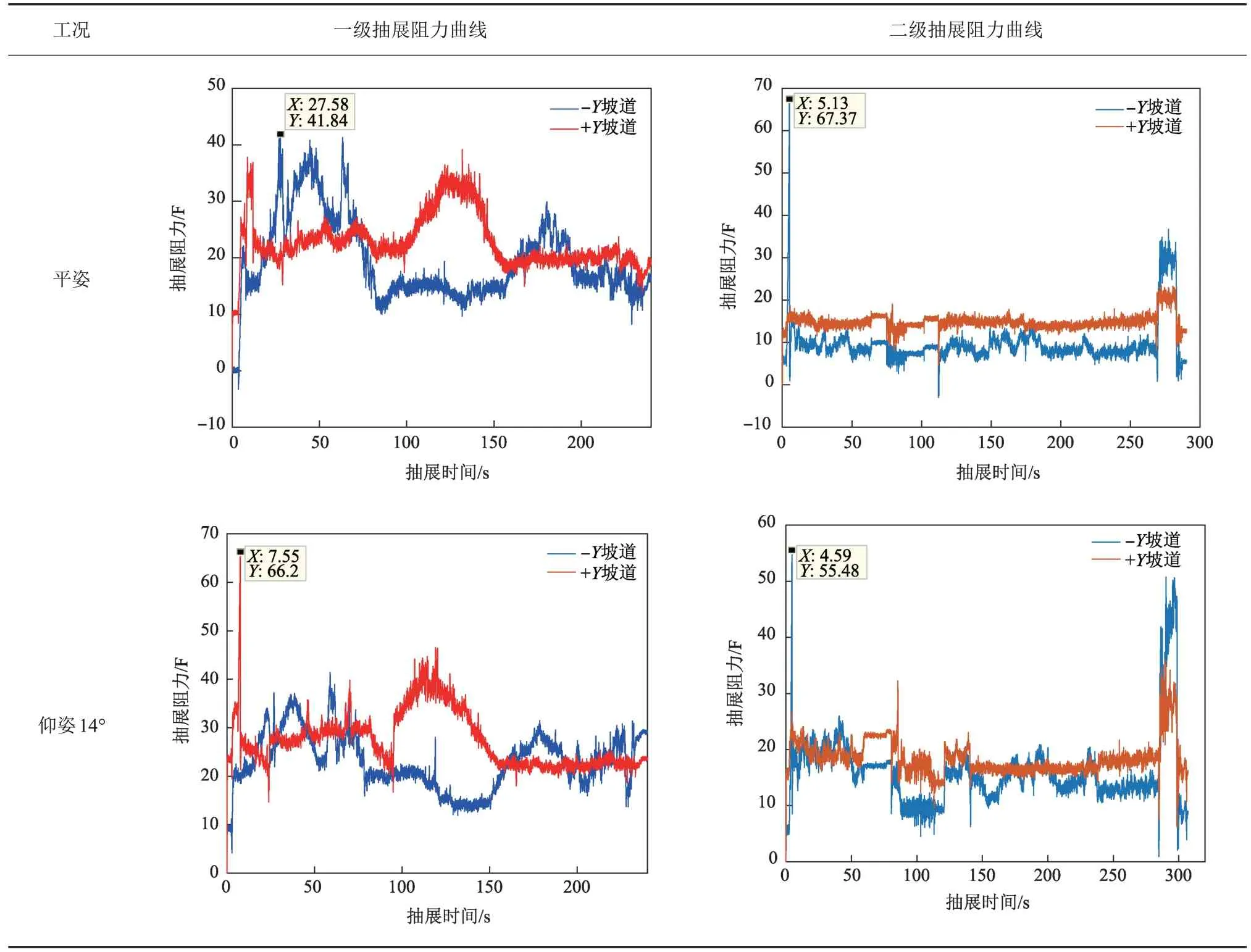
表2 抽展阻力曲线Table 2 The curve of pumping resistance
4.4 驱动裕度分析
根据抽展阻力数据,测试结果如表3~4所示,2种工况下的抽展阻力远小于额定驱动力300 N的设计值,驱动裕度最小值为2.5,满足航填驱动裕度规范1.5的要求。

表3 一二级抽展阻力裕度Table 3 The resistance margin of first and second level drawing

表4 摆转临界态抽展阻力裕度Table 4 Swinging critical state draw resistance margin
5 结 论
针对着陆器包络限制,提出一种重叠布局的双向抽展式火星车转移坡道方案,解决了大展出比、驱动共用、可靠展开等关键问题,对其展开原理及力学特性进行分析,并开展了模拟火星重力环境的展开试验,可为我国火星车转移坡道设计提供参考。

