地月空间信息网络链路分配算法研究

刘冰怡，王璐琦，郭 薇，朱维各

（1.上海交通大学区域光纤通信网与新型光通信系统国家重点实验室，上海 200240；2.上海卫星工程研究所，上海 200240）

引 言

对月球的探测是人类向深空迈出的第一步。早在20世纪60年代，美国和前苏联就开始了一系列对月球的探测活动。从21世纪初开始，许多国家也纷纷开展各自的探月研究项目，深空探测也被列为中国21世纪发展战略之一。

2018年5月21日，中国发射了“鹊桥号”卫星，该卫星围绕月球背面的地月拉格朗日点运动，采集到的月球背面的科学数据，由“鹊桥号”中继，以点对点的通信方式，通过星地链路回传到地面站。当地面站随着地球自转运动到与鹊桥号卫星不可见的位置时，通信链路中断。在通信链路中断时间段内，鹊桥号采集到的数据将无法回传。由此可见，该地月通信架构无法满足面向月球的全时域、多节点、全覆盖的通信要求[1-2]，无法支持未来日益复杂的人类探月活动所带来的遥测、遥控、导航、语音等通信类业务。

孙晨华等[2-3]指出，由多颗月球中继卫星、地球中继卫星和地面站组成的地月空间信息网络在对星球的覆盖范围、测控时间、传输可靠性、节点冗余性等方面较其它地月通信架构更有优势。然而基于该架构下，目前并没有研究具体指出应该构建一个怎样的地月空间信息网络拓扑。

在设计卫星网络拓扑时，通常关心的性能指标有网络的平均点到点通信延迟（在卫星网络中，传播时延是产生通信时延的主要因素[4]）、网络连通性等。本文设计的地月空间信息网络旨在为地球与月球之间的通信类业务提供远距离中继服务，主要关注地月之间的通信质量。因此，在设计网络拓扑时，选择平均月球中继卫星节点到地面站的路径距离来计算该网络的平均传播时延，并以最小化该平均距离为优化目标，以满足未来地月遥测、遥控、语音和视频等实时通信类业务的需求。同时为了使该网络能够为地月之间提供持续通信，设计拓扑时还应满足月球中继卫星与地面站之间的连通性约束，即每颗月球中继卫星总存在一条到地面站的连通路径。

因功率、重量和成本等因素的限制，每颗卫星所允许携带的通信终端数目是有限的（建立一条链路的同时需要占用该链路两端节点上各一个通信终端），但是能够与这些卫星建立通信链路的节点数目往往超过其所携带的终端数目。因此，如何分配每个卫星节点上有限的通信终端建立链路，从而构建一个性能良好的地月空间信息网络拓扑，成为了一个有意义的研究问题。

本文所研究的网络拓扑设计问题即通信链路的分配问题。对此，针对由多颗月球中继卫星、地球中继卫星和地面站节点组成的地月空间信息网络，本文设计了两种链路分配算法：基于竞争决策思想的链路分配算法（Link Assignment Algorithm Based On Competitive Decision，LAA-CD）和基于模拟退火法的链路分配算法（Link Assignment Algorithm Based On Simulated Annealing，LAA-SA），旨在解决地月空间信息网络卫星通信终端数目有限情况下的链路分配问题。算法以最小化平均月球中继卫星节点到地面站距离为优化目标，在保证月球中继卫星与地面站连通性的同时，每颗卫星所连接的链路数目不超过其携带的通信终端数目。

在地月空间信息卫星网络中，卫星与卫星、卫星与地面站之间的可见性随着地球自转和卫星运动而不断变化，只有当两个节点彼此可视时，才有可能建立链路。因此，每个节点将会随着与其可视的节点集合的变化而动态地建立和删除链路。为了便于为一个动态的网络设计拓扑，将一段时间内的网络划分为若干个时隙如图1（a），时隙的划分由可见关系的变化触发，一个时隙内所有节点之间的可视关系不发生变化。图1（b）分别对应图1（a）中时隙i和时隙j下的可视关系，虚线表示节点之间可视，当S3 运动到与S4可视的位置时，即进入一个新的时隙。

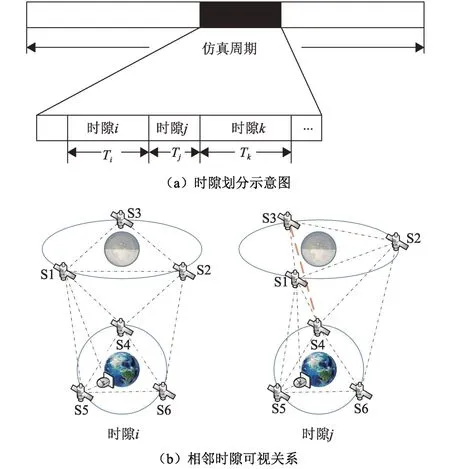
图1 时隙的划分Fig.1 Division of time slots

1 相关研究

目前，网络链路分配问题的研究对象主要包括某些具有高动态性的网络（如Ad Hoc 网络、传感器网络）和近地卫星网络。在以Ad Hoc 网络或传感器网络为研究对象的拓扑设计研究中[5-7]，拓扑设计的优化目标通常为提高网络连通性、降低能耗等。文献[8]以最小化地面站管理资源为优化目标，提出了一种基于烟花算法的链路分配算法，但是没有考虑卫星终端数目的约束；Lansard等[9]针对由低轨、中轨卫星组成的网络，介绍了距离优先的贪婪链路选择策略；Liu 等[10]中要求将每颗卫星上所有的终端都用于建立星间链路，提出了一种基于拓扑图完美匹配模型的链路分配算法；Tan等[11]提出了一种通过为可视的卫星之间随机分配星间链路，直到被通信终端的占用率达到某个给定值的链路分配算法；NOAKES 等[12]以保证网络拓扑整体的连通性为目标，设计了一种针对动态卫星网络的链路分配算法，根据网络状态的变化决定链路的建立和连接；Harathik等[13]针对具有两个轨道平面，并且两个轨道平面上的卫星数目相同的卫星星座，以最大化通信终端的利用率为优化目标，研究了当卫星的可视节点数目多于其星载通信终端数目情况下的链路分配问题；Watts 等[14-16]的链路分配算法均以平均点到点距离最小为优化目标，但是都没有考虑到该方法实际情况下卫星上终端数目的约束，且计算平均点到点距离最小的优化目标并不适用于地月通信场景；Fraire 等[17]的算法虽然能够提高拓扑的连接密度，但是仍然不能保证网络的连通性；Huang等[18]针对DTN（Delay Tolerant Networks）卫星网络，考虑到卫星节点可视关系动态变化的特点，以最小化连接数为优化目标设计拓扑，但仍然忽略了通信终端数目的约束。

上述链路分配相关研究并没有综合考虑卫星网络拓扑设计问题中的多个因素，如平均时延、卫星所携带的通信终端数目限制、连通性等，且在平均时延和连通性的定义上，地月空间信息网络拓扑不同于其他网络，本文关注的是月球中继卫星与地面站之间的平均距离和连通性，而非所有网络节点之间的平均距离和连通性。因此，以上研究中的算法并不适用于本文研究场景，需要设计一种针对地月空间信息网络场景的链路分配算法。此外，地月空间信息网络方面的研究大多关于卫星星座架构设计方面，具体拓扑设计的研究目前仍出于空白阶段。

2 基于竞争决策思想的链路分配算法（LAA-CD）和基于模拟退火法的链路分配算法（LAA-SA）

2.1 符号说明

地月空间信息网络链路分配问题中的参数和含义如下：

vstation：地面站节点；

Vm：月球中继卫星节点集合；

Ve：地球中继卫星节点集合；

m：月球中继卫星数目；

n：地球中继卫星数目；

N：每颗卫星允许携带的通信终端数目上限；

d(v)：卫星节点v的度数，即v所连接的链路的条数，v∈Vm∪Ve；

V：加权可视矩阵。当节点i和j彼此之间可视时，V(i,j)大小等于i与j之间的距离；反之，V(i,j)=∞；

G：网络拓扑矩阵。当为节点i和j之间分配了一条链路时，G(i,j)=V(i,j)；反之，G(i,j)= ∞；

a(i,j)：表明节点i和j之间是否连通。当i和j之间存在至少一条通路时，a(i,j)= 1，否则a(i,j)= 0；

p1(i,j)：节点i到j的最短路径；

dist(i,j)：表示p1(i,j)的距离；

h(i,j)：从节点i到j最短路径的跳数；

p2(i,j)：节点i到j的次短路径；

distsec(i,j)：表示p2(i,j)的距离；

n(v)：v∈Vm，表示月球中继卫星v到vstation的最短路径与其它月球中继卫星到vstation最短路径的公共节点数目。

2.2 数学模型

基于上述问题描述和符号说明，地月空间信息网络链路分配算法的优化目标可以表示为

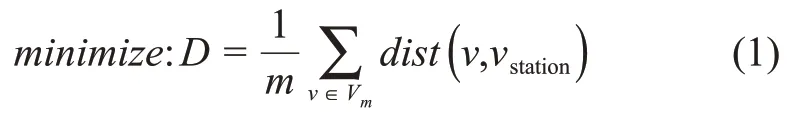
约束条件为

由于每颗卫星携带的终端数目是相同的，且链路是双向的，上述加权可视矩阵V和网络拓扑矩阵G均是一个大小为(m+n+ 1)×(m+n+ 1)的对称矩阵。利用Dijkstra 算法，可以计算出每颗月球中继卫星到地面站的最短路径距离。

约束条件C1 确保了网络的连通性，即每颗月球中继卫星都存在一条与地面站之间的连通路径；C2则是考虑到了卫星携带终端数目的限制，在设计算法的过程中需要保证每颗卫星连接不超过N条链路。

2.3 基于竞争决策思想的链路分配算法LAA-CD

在设计链路分配方案的过程中，为了减少月球中继卫星节点到地面站路径的平均长度，希望尽可能缩短每颗月球中继卫星到地面站的路径。当根据加权可视矩阵V计算出多个月球中继卫星到地面站对应的路径都经过某个卫星节点，以致超出其度数约束时，为这些路径所经过的节点之间分配链路显然是不合理的。如图2（a），假设卫星的度约束为4，图2中月球中继卫星S1、S2、S3到地球中继卫星S4的带箭头虚线表示它们到地面站的最短路径所需要经过的一段可视链路，黄色连线表示已经存在的链路，可见若按照每个月球中继卫星的最短路径向经过的节点之间分配链路，S4 将超出其度约束（称在节点S4 发生冲突），3颗月球中继卫星中必然将至少有一颗不能够与S4建立星间链路，该情况下各个月球中继卫星之间存在着对节点S4的竞争

图2 超出节点度约束情况示意图Fig2 Schematic diagram of exceeding the degree constraint

为了解决上述问题，设计了一种基于竞争决策思想[19]的链路分配算法LAA-CD。竞争决策算法模拟了一种多个竞争者竞争一个或多个资源的过程，按照优胜劣汰的决策原则使一部分竞争者获得资源而增加实力，另一部分竞争者失去资源而减弱实力甚至死亡。决策算法由以下几部分组成：①竞争力函数：代表竞争者对某种资源具有的竞争力；②决策函数：根据竞争力函数值的大小来决定把资源分配给哪一个竞争者；③初始格局——在某一轮竞争开始前各个竞争者对资源的占有情况。算法通常设计多个竞争力函数、决策函数和初始格局，共进行round（round=竞争力函数个数·决策函数个数·初始格局个数）轮竞争，最后根据目标函数选取较优解。

在本文的LAA-CD算法中，共有m个竞争者，即所有的月球中继卫星。初始格局下不为网络分配额外的链路，且a(v,vstation)= 0,∀v∈Vm，即在初始拓扑矩阵G下，所有竞争者都无法与地面站连通。可以根据每一轮的竞争力和决策函数，依次为每个竞争者分配资源，即为当前竞争者向拓扑矩阵G中分配的其最短路径所经过的链路。当然，在分配链路的过程中，需要保证每个卫星节点的度数不超过N，因此本算法中引入了一种可视关系删除的做法，在为每一个竞争者分配资源前，都需要找出当前d(v)=N的节点v和与v可视但是彼此之间未分配链路的节点u，并从当前的加权可视矩阵V中删除v和u之间的可视关系，如图2（b）。令V(v,u)= ∞，那么在为下一个竞争者分配资源时，将不可能另外分配一条与节点v相连的链路，避免了v超出度约束问题的发生。竞争结束时，每个竞争者都分配了一条到地面站的路径，且满足了约束条件C2，得到一种链路分配方案。

2.3.1 竞争力函数

本算法采用如下4个竞争力函数为

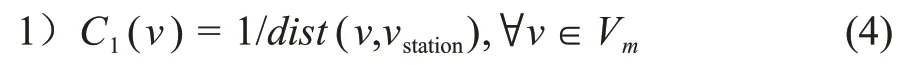
卫星节点v到vstation的最短路径的距离越小，竞争力越大，则越应该优先分配这条最短路径所经过的链路。

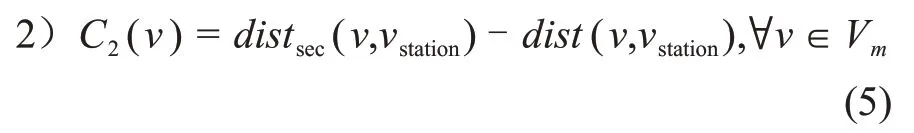
根据Yen算法分别求出次短路径与最短路径的长度，且二者差值越大，说明由于拒绝该竞争者的最短路径而增加的距离越大，因此可以考虑优先分配该竞争者的最短路径所经过的链路。

竞争者v到vstation最短路径与其他竞争者到vstation最短路径的公共节点数越少，那么在所经过的中间节点发生冲突的概率则越小，其竞争力可能更大。

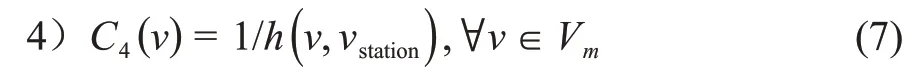
竞争者v到vstation最短路径的跳数越少，发生节点冲突的概率越小，竞争力越大。

2.3.2 决策函数

本算法采用如下两个决策函数

1）根据初始的加权可视矩阵V计算出每个竞争者的竞争力，按照从大到小排序依次向拓扑矩阵G中分配每个竞争者由加权可视矩阵V计算得到的最短路径所经过的链路；

2）每为一个竞争者分配最短路径后，根据更新的加权可视矩阵V重新计算剩余竞争者的竞争力，选择当前最具竞争力的竞争者分配资源，直到没有竞争者剩余。

2.3.3 算法流程

算法流程如图3所示。

图3 LAA-CD算法流程Fig.3 Algorithm flow of LAA-CD algorithm

2.4 基于模拟退火法的链路分配算法LAA-SA

文献[20]～[21]研究了在不考虑卫星终端约束下的卫星网络链路分配问题。模拟退火算法在得到一个新的解时，若新解的目标函数值优于旧解，接收新的解；反之，则以一定的概率来接受一个比当前解要差的解，从而有可能跳出局部最优解。接收较差解的概率为

其中：ΔD表示新旧解目标函数的差值大小；温度参数T在每一次迭代后，乘以某个小于1的降温系数逐渐减小。

当迭代次数达到上限或目标函数不再改善时，停止迭代。算法流程如图4 所示。在选择初始拓扑时，以任意顺序依次为网络中的卫星随机选择可视节点并建立链路。当某颗卫星的可视节点（且有空闲终端）数大于其空闲终端数目时，与该卫星所连接的节点数等于其空闲终端数目；当可视节点数小于剩余终端数目时，则与其所有可视节点建立链路；当某颗月球中继卫星与地面站可见时分配一条星地链路。然后通过分支交换的方式，如图5产生一个新的拓扑，并迭代若干次的退火过程。

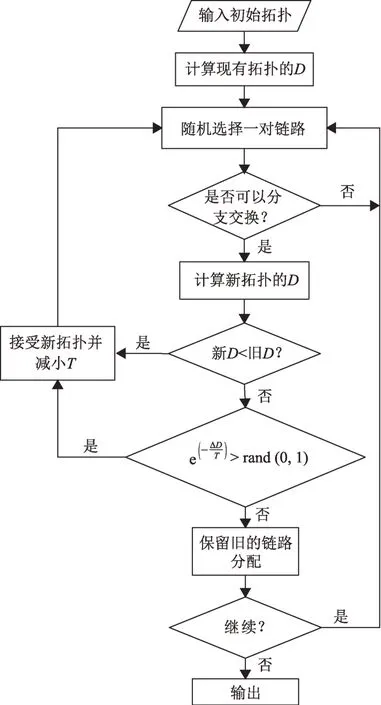
图4 LAA-SA算法流程图Fig.4 Flowchart of LAA-SA algorithm

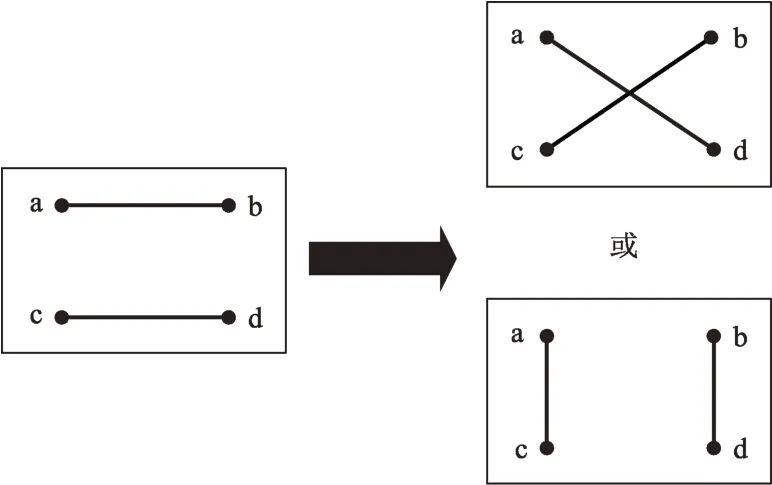
图5 分支交换Fig.5 Branch and exchange

3 实验仿真与分析

本节中对比分析了LAA-CD、LAA-SA 和LAA-greedy算法在月球中继卫星到地面站路径的平均距离D方面的性能。假设每颗卫星允许携带的终端数目上限N为4。在LAA-SA 算法中，根据多组参数设置下的实验结果对比，发现当设置退火前的初始温度为1 000、降温系数为0.99 且迭代次数为50 次时，能够得到最小的D在仿真时间段内的均值-D，因此选择在此参数设置下与LAA-CD 和LAA-greedy 进行对比。LAA-greedy 算法基于优先为到地面站路径距离较短的卫星分配路径的思想，依次为该最短路径所经过的节点之间分配链路

为了考察算法的有效性，同时保证中继卫星能够对月球表面和地球表面的全覆盖，选择了两种目前提出较为可行的中继卫星星座，如表1所示。

表1 卫星星座构成Table 1 Satellite constellations

6颗月球极轨道卫星的轨道参数[3]如表2中所示，4 颗围绕以地月拉格朗日点卫星围绕以L1、L2、L4和L5 为中心的Halo 轨道运行[22]，地球中继卫星星座包 含 3 颗 GEO 卫 星 ， 分 别 位 于 110°E、 10°W 和130°W。设置地面站位于北京 （N38°39′6.48″，E104°04′35.11″）。假设在进行分配链路前，位于同一轨道平面内的3颗卫星之间已经存在固定的星间链路，4颗地月拉格朗日点卫星之间连成一个环状，且GEO1存在一条到地面站的固定的星地链路。

选择未来2020年1月1日0点－2020年1月2日0点内的网络情况进行仿真实验。在一个时隙内，以15 min的时间间隔粒度对所有节点之间的距离进行采样（若该时隙时间长度大于15 min），最终得到仿真时间内各时隙起止时间点和采样时间点下的距离数据并计算。

表2 月球极轨道卫星轨道参数Table 2 Orbit parameters of polar orbit satellites

3.1 链路分配算法性能对比

1）基于月球极轨道星座的链路分配算法对比

在星座1 下，对比了3 种算法在月球中继卫星到地面站平均距离D方面的性能。仿真结果如图6所示。对LAA-CD、LAA-SA 和LAA-greedy 算法得到的D计算仿真时间段内的均值，得到的分别为 4.388 9× 105km、4.382 7× 105km 和 4.437 9×105km。

图6 星座1下LAA-CD、LAA-S和LAA-greedy算法性能Fig.6 Algorithm performances of LAA-CD、LAA-SA and LAA-greedy in Constellation 1

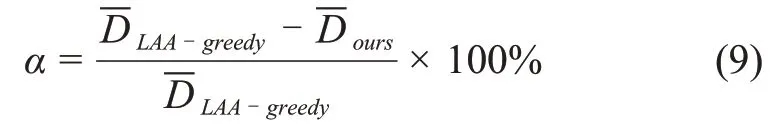
根据仿真结果计算可知，LAA-CD和LAA-SA算法得到的α分别约为1.1%和1.2%，可见LAA-SA 和LAA-CD 均优于 LAA-greedy，且 LAA-SA 算法略优于LAA-CD。

2）基于地月拉格朗日点Halo轨道星座的链路分配算法对比

分析实验结果发现，在两种星座下LAA-SA 和LAA-CD算法所的到的拓扑的月球中继卫星到地面站路径平均距离总是小于LAA-greedy。同时，横向对比本文提出的两种算法，发现LAA-CD算法在平均距离方面略大于LAA-SA算法，但是能够极大降低算法的时间复杂度，在星座1 下的算法运行时间约为LAA-SA的1/6，星座1下约为LAA-SA的1/13。这是因为LAA-SA算法需要随机选择一对链路进行分支交叉变换，并循环若干次后才能获得较优解，而LAACD 算法通过引入若干个竞争力函数和决策函数，使得算法能够更具有目的性、更高效地寻找到新的较优解。

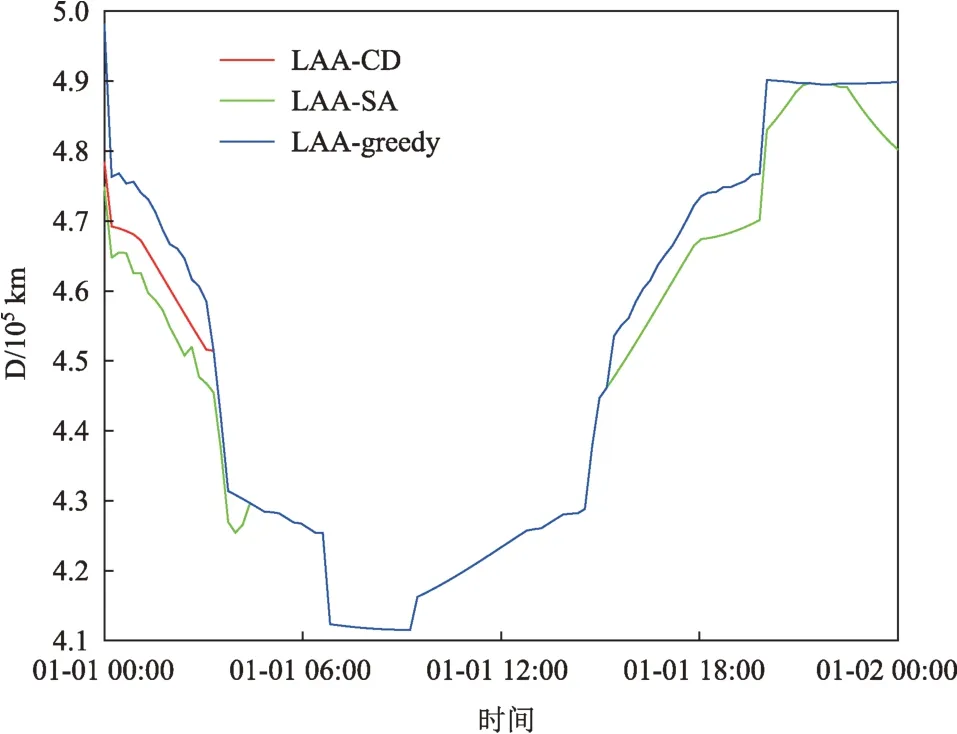
图7 星座2下LAA-CD、LAA-SA和LAA-greedy算法性能Fig.7 Algorithm performances of LAA-CD、LAA-SA and LAA-greedy in Constellation 2

3.2 卫星终端数目约束对算法性能的影响

上节的实验结果是基于所有卫星所搭载的通信终端数目均相同时的条件下得到的。然而，当每个卫星上的通信终端数目不相同时，本文提出的LAA-SA和LAA-CD算法是否仍然具有较好的性能呢？因此，本小节将主要考虑不均等的星上通信终端分配对算法性能的影响，分别在2种星座构成下对比了3种算法在月球中继卫星到地面站平均距离D方面的性能表现。

当某颗卫星上的某个或某几个通信终端出现故障时，如果此时把该条星间链路所连接的另一端的卫星上的通信终端关闭，这样很有可能会对网络的整体性能产生巨大影响，同时也是对星上通信终端资源的一种浪费，因此需要考虑重新进行链路分配。本小节侧重于如何在通信终端数约束不同的情况下分配链路。在星座1 中，随机选择2 个仅有2 个通信终端正常工作的卫星节点，和3个仅有3个通信终端正常工作的卫星节点，即随机产生2 个f(v)= 2，∀v∈Vm∪Ve的卫星节点和3 个f(v)= 3，∀v∈Vm∪Ve的卫星节点，剩下5个f(v)= 4，∀v∈Vm∪Ve的卫星节点。

根据仿真结果，在星座1下，三种算法得到的D的均值分别为 4.638 4× 105km、4.5514× 105km和4.9658× 105km，LAA-CD和LAA-SA算法的性能提升比率α分别约为6.6%和8.3%。类似的，在星座2下，分别为 5.258 7 × 105km、5.1331× 105km 和5.412 4 × 105km，LAA-CD 和LAA-SA 算法的性能提升比率α分别约为2.8%和5.2%。由此可见，在星载通信终端数目不等的情况下，本文提出的两种LAASA和LAA-CD算法仍然均优于LAA-greedy。

3.3 星座架构对比分析

两种星座的性能对比如表3。基于本文实验结果，可以得出以下结论：基于月球极轨道卫星的星座相比地月拉格朗日点Halo 轨道卫星星座，具有更短的平均月球中继卫星到地面站距离。

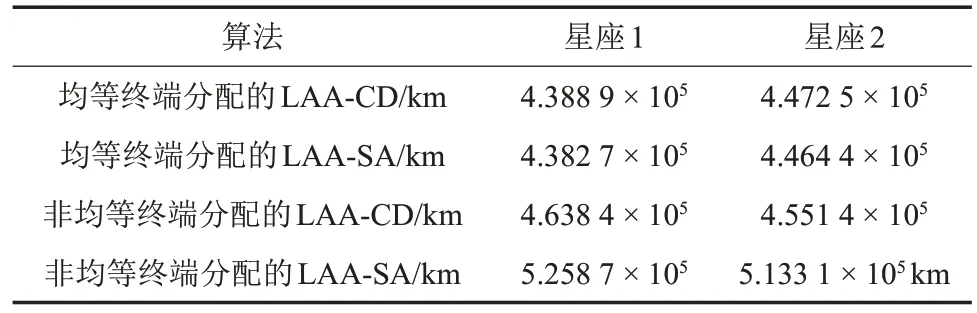
表3 两种星座下的性能对比Table 3 Performance comparison between two constellations

4 结 论

本文针对由多颗月球中继卫星、地球中继卫星和地面站组成的地月空间信息网络中，卫星可视节点数目多于所携带的通信终端数目时的拓扑设计问题，提出了基于竞争决策思想的链路分配算法LAA-CD和基于模拟退火法的链路分配算法LAA-SA，并与贪婪算法进行了对比。实验结果证明，LAA-CD与LAA-SA均比贪婪算法具有更小的平均月球中继卫星到地面站距离。同时，LAA-CD算法相比LAA-SA具有较低的时间复杂度，而LAA-SA算法能够得到更小的平均距离。通过实验对比两种星座架构，可以发现，若从降低地月通信时延的角度出发，构建一个基于月球极轨道卫星星座的地月空间信息网络拓扑更为合适，可为地月空间信息网络分配提供技术支持。