摭谈数学模型构建的教学策略
陈荔丹
摘 要:小学数学教学关注数学模型的建构,有利于促进学生数学思维的发展,凸显学生的数学思考能力及问题解决能力,提升学生的学科素养。教师可以帮助学生在问题情境中建模、在探索规律中建模、在归纳推理中建模、在数形结合中建模、在解决问题中建模。
关键词:数学模型;学科素养;构建策略
《义务教育数学课程标准(2011年版)》明确提出:模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。因此,在教学过程中教师应充分重视发展学生的数学模型思想,帮助学生初步构建各种形式的数学模型,架起数学基础知识与数学应用之间的桥梁,提高学生学习数学的兴趣和应用意识,训练学生的数学思维,发展数学素养。下面从几个视角就在小学阶段如何构建数学模型,与同行共同商榷。
一、在问题情境中建模
数学知识的形成是从生活实践活动中逐步积累的结果,从学生生活经验出发去理解学习内容是小学数学学习的重要特征。教學中,教师要有意识地根据教材内容,有针对性地创设有利于引发学生数学思考的教学问题情境,以激活学生处于休眠状态的原有认知,促使学生的思维处于上升状态,引发其问题意识和探究欲望。在问题情境中有机地渗透模型思想,让学生在实践、探究、运用等活动中梳理出问题模型,形成一种解题模型的技能,发展模型思维,从而实现数学认知更系统、更完整。当学生在实际问题情境中完成建模后,紧接着教师进行“去情境化”的数学活动,紧紧突显所学数学知识的本质属性,实现从生活数学向学科数学抽象,从而真正完成建模的过程。例如,“鸡兔同笼”问题最初的教学就是在问题情境中研究:笼子里有若干只鸡和兔。从上面数有8个头,从下面数有26条腿。鸡和兔各有几只?学生凭借生活经验,知道鸡有2条腿,兔有4条腿,再根据问题情境,通过列表尝试,不仅解决了问题,得到鸡有3只,兔有5只;还逐渐明白了鸡兔只数虽然在不断变化,但腿的条数是不变的,从而发现构建了“2×(鸡只数)+4×(兔只数)=总脚数”这个数量关系模型,有了这个数量关系模型,就为“鸡兔同笼”的方程解和其他类似的数学问题奠定了基础。
二、在探索规律中建模
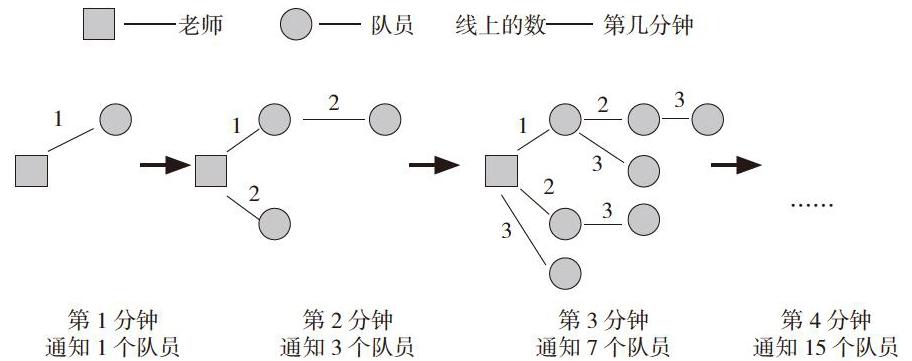
探索规律是小学数学知识结构的一项组成内容,在探索规律教学中,教师要重视让学生自己经历观察、猜想、分析、类比、抽象、概括、归纳等数学思维活动过程,在充分尊重学生主体作用的基础上,发挥教师的主导作用,把规律从具体的情境中抽象出一般模型,实现对抽象知识和数学思想、方法的理解与掌握,从而让学生把外化的行为与内在的思维活动结合在一起,在发现数学规律中完成建模,发展数学思考能力。例如,人教版五年级下册“打电话”教学,本节课重点是研究如何在最短时间内通知到所需的队员。学生先列举多种方案,然后通过观察、比较、类推、概括、抽象等思考活动,发现要使时间用得最少,就需要每个知道信息的人又立即通知别人,每个人都不能闲着。教学时,教师可以借助画图,运用数形结合的方法让学生直观形象地观察每分钟通知到的队员:
教师再引导学生对每分钟通知到的队员1、3、7、15……这组数列进行研究,并思考:为什么第1分钟只有1个队员知道,第2分钟就有3个队员知道……结合图画直观,学生很快会明白已接到通知的队员每人每分钟都再通知一个。最终发现:后1分钟接到通知的人是前1分钟知道信息队员的2倍再加老师也再通知的1个,也就是说,后1分钟接到通知的人是前1分钟知道信息队员的2倍加1,即第n分钟接到通知的队员和老师的总数是(n-1)分钟所有接到通知的队员和老师的总数的2倍。学生在探索“打电话”的规律中,构建了这种“倍增”的数学模型,训练发展了数学思维,为后续解决同类问题提供了思路与策略。
三、在归纳推理中建模
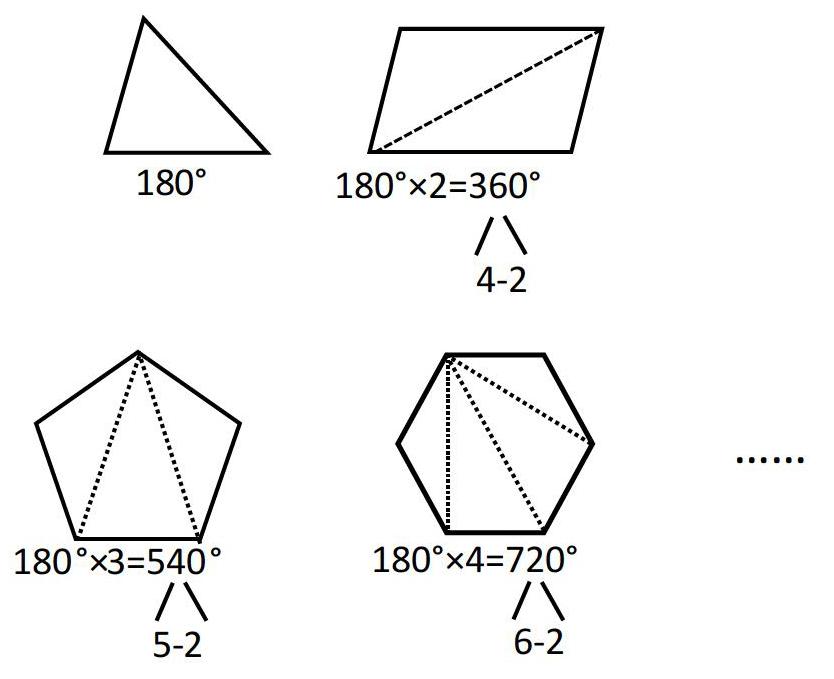
归纳推理是一种由个别到一般的推理,它是由一定程度的关于个别事物的观点过渡到范围较大的观点,由特殊具体的事例推导出一般原理、原则的解释方法。归纳推理建模,需理清要解决的问题,收集相关的信息、背景等,根据收集的材料,探寻要解决问题的相连认知基础。从似乎无规律的情况中抽取合适的内容,进行模型数据、形状以及其他资料的对比,进而找到规律,分析求解。最后进行模型的验证与应用,通过应用模型,查看其合理性,从而发展数学素养。例如,四年级下册求多边形的内角和(如下图):
学生从图中发现,要求解多边形内角和,原来是把多边形分割成若干个三角形,然后用三角形的内角和乘三角形的个数就行了,而多边形分割成的三角形个数是(边数-2),学生通过观察、分析、概括,归纳出:多边形的内角和是180°×(n-2),这个数学模型的建立就水到渠成了。
四、在数形结合中建模
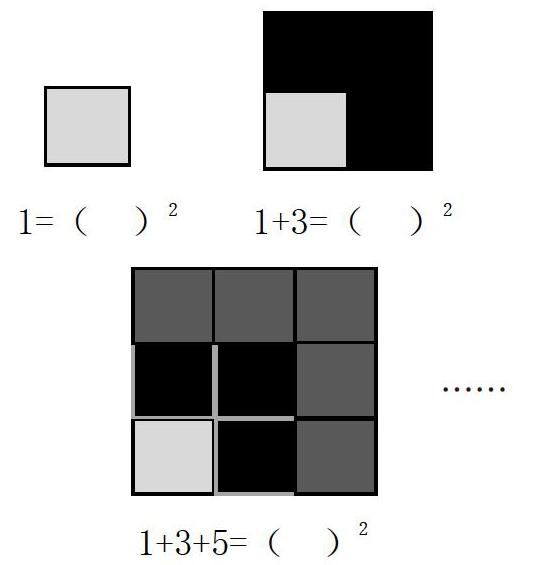
形的问题中包含着数的规律,数的问题也可以用形来帮助解决,数与形在一定条件下可以相互转化。数学学习中,学生通过数与形的相互结合,可以把抽象思维转换成形象思维,使复杂问题简单化、抽象问题具体化,借助图形发现数的规律,从而建立数学模型。例如,人教版教材六年级上册第107页例1:
教学这道题时,借助摆正方形,从形引入,让学生观察说出每次增加了几个小正方形,3个大正方形分别有几个小正方形,用加法算式是1,1+3,1+3+5……;用乘法表示是1×1=12,2×2=22,3×3=32……。接着引导学生把数与形相互对照,思考:算式左边的加数排列有什么特点?在图中分别表示什么?左边对应的右边平方数又是图中的什么?如果照这样摆下去,第4个、第5个……正方形分别要摆几个小正方形?用加法算式与乘法算式分别要怎样表示?最后组织学生分组讨论:第n个大正方形包含的小正方形数应该是多少?你发现了什么规律?通过数形结合的相互转换,学生就能直观、简单地构建1+3+5+……+(2n-1)=n2这个数学模型。
数与形中隐藏着许多非常有意思的规律,容易引起学生的探究兴趣,教师在教学时要充分利用机会,一方面,要培养学生积极的数学学习情感;另一方面,让学生体会数学思想的价值与魅力。
五、在解决问题中建模
学生在解决问题时,通常要经历根据数学问题情境、理解与简化问题信息、综合运用数学知识与技能、分析问题结构、概括其中蕴含的数量关系、建立解决问题模型的过程,最后运用建立的模型解决类似的数学问题,提高知识运用能力和数学应用意识,形成并灵活运用数学思想、数学方法和解题策略,发展数学思考能力。因而,教师在解决问题的教学过程,要强调基于数学建模理念下的数量关系分析,关注数学模型的建构,促进学生知识的同化与顺应,有效培养学生触类旁通、举一反三的数学能力。例如,这样几道应用问题:
(1)一块长方形地的周长是80米,宽是10米,长是多少米?
(2)小明买两套课桌椅花80元,已知每把椅子10元,每张桌子多少钱?
(3)甲、乙、丙三个人去植树,甲种80棵树,乙种10棵树,甲种的棵数刚好是乙、丙种的总棵数的2倍。丙种多少棵树?
上述几道题看似素材、内容各不相干,但学生通过解决问题,发现这几道题的题目结构、数量关系、解题策略是相同的,即它们都是已知两个数的和的2倍是多少与其中一个数,求另一个数的数学问题,解决这几道题用算术解都是80÷2-10,列方程式都是(x+10)×2=80。这样便建立起了此类问题的数学模型,再设计几道数量关系类似的问题让学生运用模型进行解答,发展了学生的应用意识和解决问题的能力,使其体验学习成功的快乐,提高学习数学的兴趣。
六、结语
小学阶段对于学生数学模型建构能力的培养,有利于促进学生数学思维的发展,凸显学生的数学思考能力及问题解决能力,提升学生的数学素养。构建数学模型,是帮助学生搭建数学基础知识与数学应用的桥梁,能有效促进学生类推、迁移等能力的发展,提升数学学科素养,它应该成为数学教育的重要方法。
参考文献:
[1]张海燕.数学建模思想在小学数学教学中的应用[J].现代教育,2015(10):88.
[2]陈 蕾.小学数学建模教学的三个关注点[J].上海教育科研,2013(8):92-93.

