一种搜索鲁棒的中国余数定理的多基线相位解缠绕技术*
蒋志彪,王 建,宋 千,周智敏
(国防科技大学 电子科学学院, 湖南 长沙 410073)
合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar, InSAR)是目前极具潜力的测绘技术之一,能够获得高分辨率和高精度的地形高程。同时多基线和多波段的InSAR技术进一步提高了InSAR 技术获取数字高程模型(Digital Elevation Model, DEM)的测量精度[1-2]。
目前,在多基线干涉合成孔径雷达信号处理步骤中,多基线相位解缠绕仍是干涉处理的关键和核心问题所在。在过去的几十年里,许多的多基线相位解缠绕方法被先后提出来[3]。文献[3]首次提出了一种基于聚类分析(Cluster Analysis, CA)的多基线相位解缠绕算法。文献[4]提出了以最大似然和最小二乘思想为基础的两种相位解缠绕方法。文献[5]提出了一种基线迭代的相位解缠绕算法,该方法通过不同基线之间的迭代,实现最终的相位解缠绕。1999年,Ferretti等将小波技术运用到相位解缠绕技术中[6],提出基于小波思路的相位解缠绕算法。随后,一些基于参数估计的多相位解缠绕方法也被相继提出来,这些方法以统计学为架构,如最大似然架构[7-8]和最大后验架构[9],但是这类以统计学为架构的多基线相位解缠绕方法都要求其干涉图数据是独立的,而且运算耗时比较大。在文献[9]的基础上,Ferraioli等为了进一步降低运算时间,提出了基于全变分(Total Variation, TV)模型和最优图割思路的优化算法[10]。
文献[11]首次将经典中国余数定理(Classical Chinese Remainder Theorem, C-CRT)运用到多基线InSAR相位解缠绕问题中,后来文献[12]对基于C-CRT的多基线相位解缠绕方法进行了应用推广,另外文献[13]将这一方法运用到了机载毫米波InSAR多基线相位解缠绕中,分析了基线构型误差和基线构型优化设计等问题。无疑,基于C-CRT的相位解缠绕方法较好解决了干涉相位欠采样处的解缠难题,然而该方法对噪声特别敏感,而实际中获取的干涉数据又不可避免地存在噪声,此问题的存在极大地限制了该方法在实际中的广泛运用。
值得注意的是,Xia等在中国余数定理方面进行了深入的研究,提出了一种鲁棒的中国余数定理[14],该方法通过搜索的方式来确定模糊数,故又称之为搜索鲁棒的中国余数定理(Searched-form Robust Chinese Remainder Theorem, SR-CRT)。该方法利用余数的冗余来鲁棒地恢复原来的数,因而具有较好的鲁棒性,故该方法广泛地运用于动目标检测、测距和频率估计等问题中[15-18]。
本文通过创新性地引入公因子,构建了新的同余方程组,将SR-CRT首次运用到多基线相位解缠绕中,并重点分析了其抗噪声性能。
1 中国余数定理原理
1.1 经典中国余数定理
设两两互质的正整数Γ1,Γ2,…,ΓL,且都大于1;a1,a2,…,aL为任意整数,n1,n2,…,nL为模糊数,一次同余方程组:
(1)
在0≤x<Γ≜Γ1Γ2…ΓL时,同余方程组有唯一解x,解的形式可以写成如下形式:
(2)

(3)

1.2 搜索鲁棒的中国余数定理
设正整数M1,M2,…,ML存在最大公约数C,且都大于1;r1,r2,…,rL为任意整数,一次同余方程组:
(4)
式中,正整数Mi满足
Mi=CΓii=1,2,…,L
(5)
考虑噪声时,即余数中存在误差,如
(6)
其中,Δri是余数误差。

(7)
式中,[·]表示四舍五入运算。模糊数ni是通过式(8)中的二维搜索方式求解,故称为搜索鲁棒的中国余数定理(SR-CRT)。

(8)
其中,
2≤i≤L
(9)
通过上述两种定理原理的对比可知, C-CRT要求同余方程组的模两两互质,而SR-CRT要求模之间具有最大公约数,且除去该最大公约数后所得的数都两两互质。
显然,两种方法对运用的同余方程组的模具有不同的要求,对于满足C-CRT进行相位解缠绕要求的基线数据,是否也可以通过SR-CRT进行相位解缠绕呢?
2 基于SR-CRT的相位解缠绕技术
对于上述问题,可通过人为引入一个公因子,构建新的同余方程组,使之满足SR-CRT的条件,下面以两幅干涉图的情形详细介绍其过程。
2.1 相位解缠绕原理
根据多基线干涉几何关系,不同基线长度下的两幅干涉图中,每一个像素都近似满足[3]:
(10)
式中:φ1,φ2为不同基线长度下的缠绕相位(去平地相位);B1,B2为不同的垂直基线长度;n1,n2分别代表两幅干涉相位图的模糊数。
利用C-CRT进行相位解缠的条件是两幅干涉图中的基线长度比值必须互质,即满足
(11)
就可以构建出同余方程组:
(12)
根据定义可得余数ai和剩余数ei分别为:
(13)
其中,⎣·」为取整运算。
对于满足C-CRT进行相位解缠的基线条件,如式(11)所示,将分子和分母同时乘以一个公因子C,可得:
(14)
联立式(10)和式(14),得:
M1(φ1+2πn1)=M2(φ2+2πn2)
(15)
将式(15)中各项提出2π,变形可得:
(16)
分别定义新的余数ri和剩余数fi为:
(17)
将式(17)的余数和剩余数代入式(16)可得:
2π(f1+r1+M1n1)=2π(f2+r2+M2n2)
(18)
将式(18)中各项对2π进行求余,可得剩余数f1和f2是相等的,最后可以构建出新的同余方程组:
(19)
只要公因子C取任意正整数,就可以利用SR-CRT求解模糊数n1,n2,得出方程组的解。
对i=1,2,考虑噪声时,即余数中存在误差,如下式
(20)
式中,Δri为余数误差。
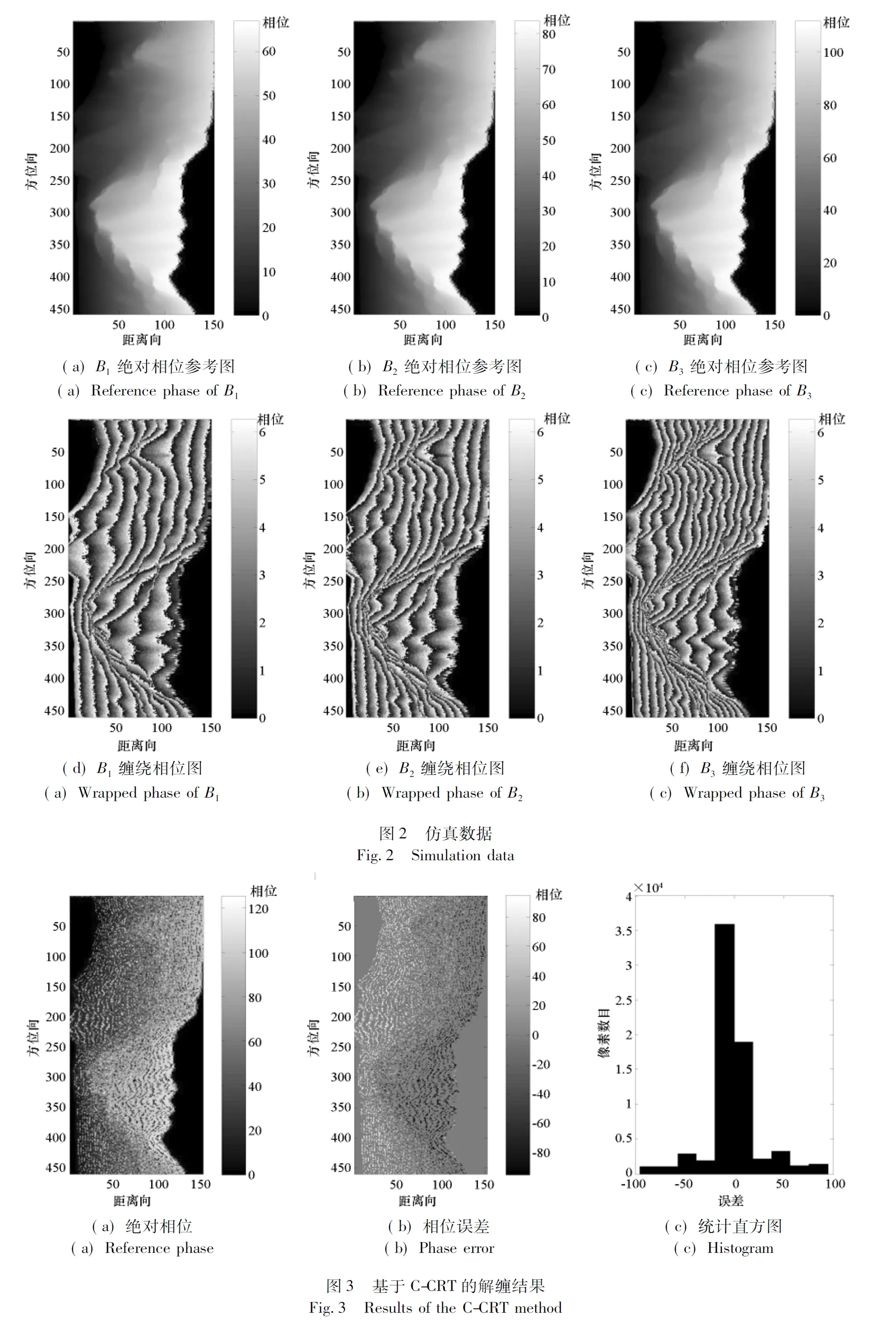
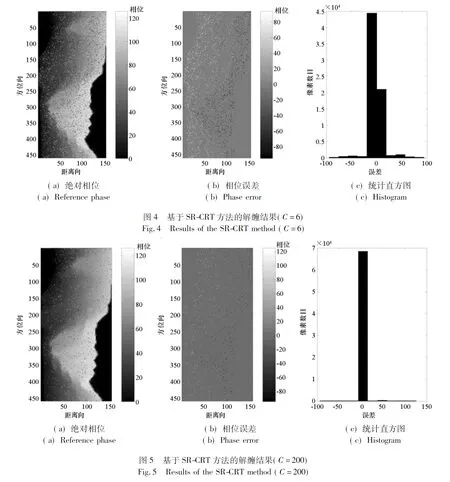
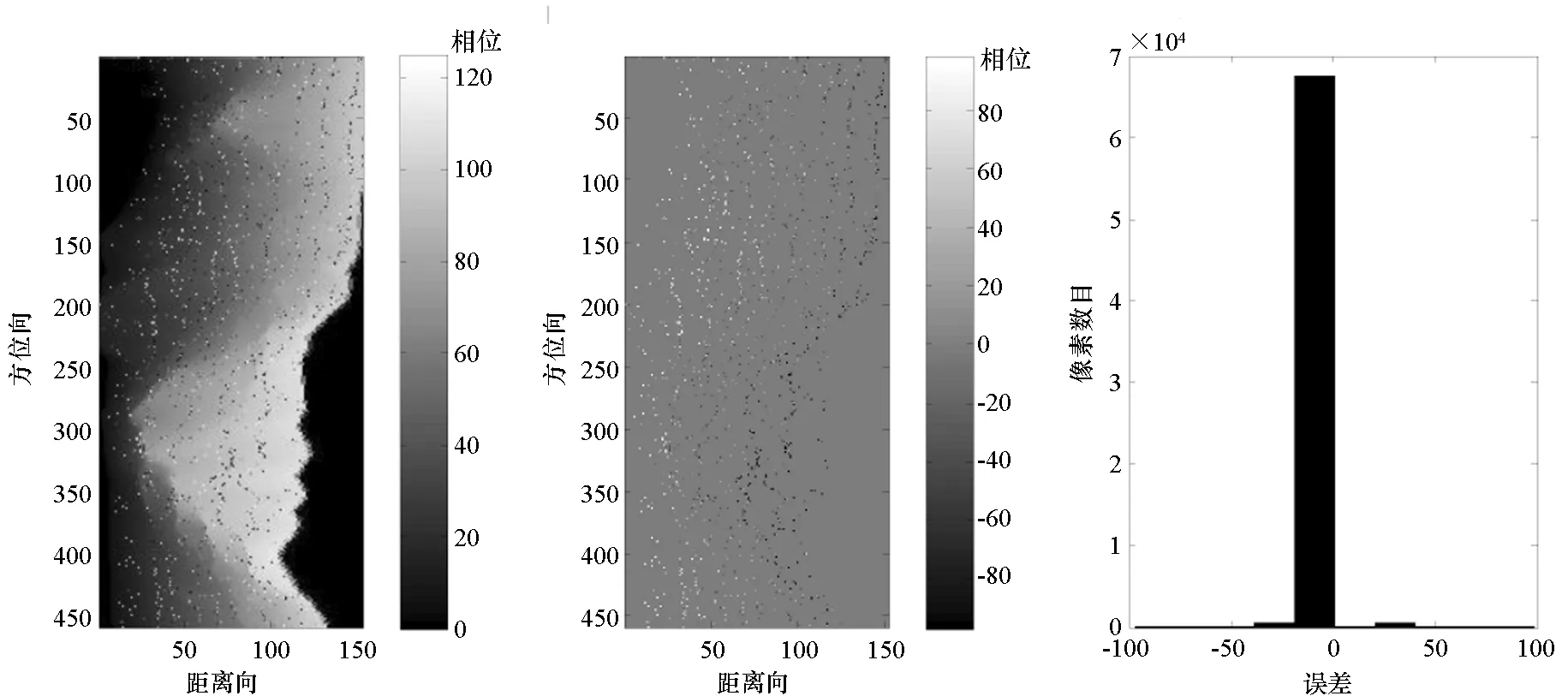
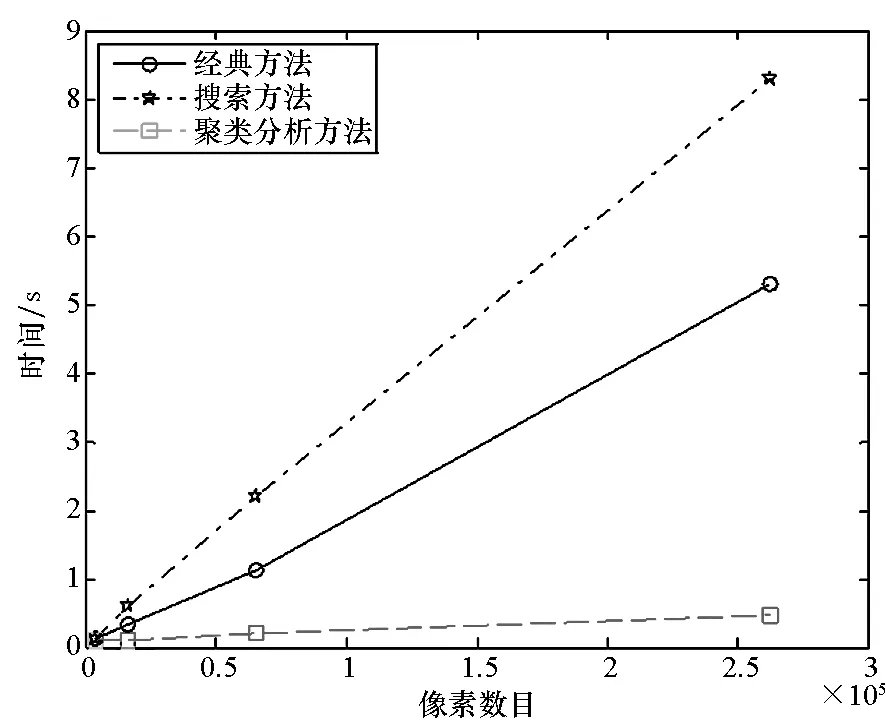
当余数误差满足|Δri|≤τ φi=φi+2niπ (21) 以上就是基于SR-CRT的多基线相位解缠绕的基本原理。 通过相位解缠原理分析可知,引入公因子后,新的同余方程组能够运用SR-CRT,那么其抗噪声性能如何? 当缠绕相位中存在噪声的情况下,可以得出: (22) 式中,Δφi是噪声相位,Δφi∈[0,2π)。 根据式(17)和式(22),可以得到有噪声的余数表达式为: (23) 又0 (24) 根据SR-CRT可知,当余数误差Δri满足|Δri|≤τ (25) 式(25)就是基于SR-CRT的相位解缠绕技术的抗噪声性能表达式,其抗噪声性能受参数Γi、剩余数fi、公因子C的影响。 需要注意的是,由于公因子C可以取任意的正整数,又0 (26) 此时噪声相位Δφi只需要满足: 0≤Δφi<π/Γi (27) 这时,基于SR-CRT的相位解缠绕技术的抗噪声性能仅受参数Γi的影响,满足式(27)条件的噪声相位的区间分布示意如图1所示。 通过噪声性能原理分析可知,基于SR-CRT的相位解缠绕技术的抗噪声性能受参数Γi、剩余数fi、公因子C的影响,而通过选择合适公因子C可以消除剩余数fi、公因子C对噪声相位的限制,从而提高该方法的抗噪声性能。 图1 噪声相位分布Fig.1 Distribution of phase noise 上述相位解缠原理是以两幅干涉图为例分析的,本节将给出其多维情况的推广。 根据多基线干涉几何关系,对于L幅不同基线的干涉相位图,同理,每一个像素也都满足[3]: (28) 式中:φ1,φ2,…,φL为不同基线长度下的缠绕相位(去平地相位);B1,B2,…,BL为不同垂直基线长度;n1,n2,…,nL分别代表在不同干涉相位图中的模糊数。 L幅干涉图中的任意两副基线的长度比值必须互质,即满足: i=1,2,…,L,j=1,2,…,L,i≠j (29) 同样,将式(29)中的分子和分母同时乘以一个公因子C,构建出新的同余方程组: (30) 定义新的余数ri和剩余数fi为: (31) (32) 只要公因子C为正整数,就可以利用SR-CRT求解模糊数,最后求出绝对相位。 通过上述基于SR-CRT的多基线相位解缠绕的基本原理分析可知,无论是二维还是多维情况,该方法都需要引入公因子C,而且公因子C可取任意正整数。下面通过试验分析公因子C的取值对基于SR-CRT的相位解缠绕技术的抗噪声性能的影响。 在上一节中,详细分析了基于SR-CRT方法的相位解缠原理和抗噪声性能,为了进一步验证该方法的有效性和抗噪声性能,本节进行性能验证实验和算法执行时间分析,并与基于C-CRT方法的相位解缠结果和文献[3]中基于CA方法的相位解缠绕结果进行对比分析,实验中验证算法的软件运行环境为MATLAB2012,计算机的CPU主频为3.2 GHz,内存为8 GB。 本实验采用由美国Long′s Peak国家公园真实数字地形高程图(图像大小为152×458)生成的干涉相位图来验证算法,实验以三幅干涉图为例来进行分析,主要系统参数如下:雷达系统天线频段为C波段,S1、S2、S3和S4分别表示四副自发自收天线的中心位置,以天线S1为参考,即S1为主天线,雷达主天线到场景中心的斜距为570 km,主天线的入射角为10.5°。三组基线的构建形式为:基线B1代表天线S1和S2对应基线的基线长度,基线B1长度为120 m;基线B2代表天线S1和S3对应基线的基线长度,基线B2长度为150 m;基线B3代表天线S1和S4对应基线的基线长度,基线B3的长度为200 m。 图2(a)~(c)分别为基线B1、B2、B3对应的绝对相位参考图。图2(d)~(f)分别为基线B1、B2、B3对应的缠绕相位图,从图中可以看出基线越长,干涉条纹越密集,其中,缠绕相位图中的相位噪声为改进的高斯噪声,考虑了地形和视数因素。 为了便于分析基于SR-CRT算法的性能,给出了基于C-CRT方法的相位解缠绕结果和基于CA方法的相位解缠绕结果做对比,并给出了公因子分别取值为6和200时,基于SR-CRT方法的相位解缠绕结果,下面以B3基线的相关解缠结果为例进行分析。 图3是基于C-CRT的多基线相位解缠绕技术的求解结果。从相位误差图中,可以明显看出解缠绕出现错误区域比较密集,并且成条纹形状,通过统计直方图可知,绝对相位误差均值为1.45,标准差为30.60,绝对相位重建误差大于2π的像素占总像素的28.22%。 图4是基于SR-CRT方法、公因子C取值为6时的求解结果。通过绝对相位图和相位误差图可知,图像两侧区域求解绝对相位与参考相位相比偏差较大,主要原因是这些区域地形比较陡峭,造成图像的相干性很低,即在图像表现出比较大的噪声,使式(25)中条件不满足,从而无法通过SR-CRT搜索到正确的模糊数,造成解缠绕结果出现错误。通过误差统计直方图可知,绝对相位重建误差均值为0.19,标准差为10.89,其中重建误差大于2π的像素占总像素的5.48%。 图5是基于SR-CRT方法、公因子C取值200时的求解结果,通过绝对相位图和相位误差图可知,除了图像两侧区域孤立的噪声点外,绝对相位图与参考相位图基本相似。通过误差统计直方图可知,误差均值为0.15,标准差为7.92,其中重建误差大于2π的像素占总像素的1.88%。 图6是基于CA方法的求解结果,通过绝对相位图和相位误差图可知,除了图像两侧区域孤立的噪声点外,绝对相位图与参考相位图基本相似。通过误差统计直方图可知,误差均值为0.06,标准差为8.85,其中重建误差大于2π的像素占总像素的2.32%。 通过图3、图4、图5的实验结果对比可知,基于SR-CRT的相位解缠绕技术的抗噪声性能明显优于基于C-CRT的相位解缠绕技术;通过图4与图5的实验结果对比可知,公因子C取值200时的求解结果要优于公因子C取值6时的求解结果,因而选择较大的公因子可进一步提高抗噪声性能。 图6 基于CA方法的解缠结果Fig.6 Results of the CA method 通过图4、图5和图6的实验结果对比分析可知,基于SR-CRT的相位解缠绕技术的抗噪声性能比较接近于基于CA相位解缠绕技术的,而且当公因子C取值合理时,基于SR-CRT的相位解缠绕技术的抗噪声性能甚至要优于基于CA相位解缠绕技术的。 下面对基于SR-CRT的多基线相位解缠技术(简称搜索方法)的算法执行时间进行仿真分析。由原理分析可知该方法是以单像素为单位进行相位解缠绕的,同基于C-CRT的多基线相位解缠技术(简称经典方法)一样,都属于单像素相位解缠绕。而文献[3]中基于CA的多基线相位解缠技术是以像素类为单位进行相位解缠(简称聚类分析方法)。图7给出了这三种方法的执行时间跟像素数目的变化关系。 图7 三种算法耗时Fig.7 Time consuming of three algorithms 从图7中可知,三种方法的执行时间跟像素数目是成正比的。通过三种方法的执行时间结果对比可知,聚类分析方法耗时最优,其执行时间随着图像尺寸增大而缓慢增加,相对而言,经典方法和搜索方法执行时间随着图像尺寸增大而快速增加。造成上述结果的主要原因是聚类分析方法是以像素类为单位进行解缠绕的,受图像尺寸的影响相对较小,而经典方法和搜索方法都是以单个像素为单位进行相位解缠绕的,因而随着图像尺寸增大,算法的执行时间明显增加。另外,搜索方法的耗时要比经典方法的耗时长,其主要原因是搜索方法需要搜索模糊数,每一个像素都需要进行式(8)这样的二维搜索,尽管文献[19-20]已经将式(8)这样的二维搜索过程简化成了一维搜索,但算法的计算复杂度在搜索次数较大的情况下仍然比较高,其耗时随着图像尺寸增大而急剧增大。 将SR-CRT首次运用到多基线相位解缠中,重点分析和研究了其相位解缠绕原理和抗噪声性能,最后通过实验验证该方法的有效性,并与基于C-CRT的多基线相位解缠绕技术进行了对比分析,总结得出了以下四点重要结论: 1)与基于C-CRT的相位解缠绕技术相比,基于SR-CRT的相位解缠绕技术中,通过公因子这一可控因素的引入(公因子可控是指公因子可取任意正整数),可以基本消除剩余数对噪声相位的限制,从而提高算法的抗噪声性能。 2)基于SR-CRT的相位解缠绕技术的抗噪声性能明显优于基于C-CRT的相位解缠绕技术的抗噪声性能,而通过选择较大的公因子可进一步提高基于SR-CRT的相位解缠绕抗噪声性能。 3)对于公因子C的取值,结合式(25)和式(26)可知,单从理论角度来说,公因子C取值越大(即正无穷大)越好,然而在实际过程中,公因子C取值可以根据式(26)中的第二个条件来确定,一般取满足条件的所有C取值中的较小值就可以使得基于SR-CRT的相位解缠绕技术获得比较满意的抗噪声性能。 4)基于SR-CRT的相位解缠绕技术是以单个像素为单位进行相位解缠绕的,对于每一个像素,都需要通过搜索来求解模糊数,算法的复杂度和搜索的次数有关,当搜索次数较大的情况下,其算法耗时随着像素数目增大而急剧增加。 上述抗噪声性能分析和结论为基于SR-CRT的相位解缠绕技术进一步在实际中的运用奠定了理论基础。后续研究将着重探讨对含有噪声的实测多基线干涉数据进行相位解缠绕以及进一步有效降低基于SR-CRT的相位解缠绕技术耗时的方法。2.2 抗噪声性能分析

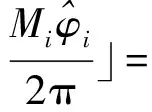

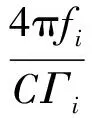

2.3 多维情况推广
3 实验结果
4 结论

