高超声速伸缩翼变形飞行器轨迹多目标优化*

彭悟宇，杨 涛，王常悦，丰志伟，涂建秋

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073； 2. 中国运载火箭技术研究院， 北京 100076)

随着任务要求及飞行环境日趋复杂化，针对飞行器的性能要求也越来越高，迫使飞行包线逐渐扩大，为了适应未来战场复杂多变的局势，变形飞行器的概念应运而生。变形飞行器是一种多功能多形态的飞行器，可以根据飞行环境、飞行剖面和任务需求进行自适应变形。变形飞行器的飞行轨迹、飞行高度和飞行速度等机动多变，飞行状态多样(如起降、巡航、机动、盘旋和俯冲等)。在不同飞行条件下执行不同飞行任务时，采用变形技术均能发挥飞行器最优的飞行性能[1]。

与传统飞行器相比，变形飞行器通过变形可以提高飞行性能，有望形成新的舵面设计和控制方法，提高飞行器操纵控制效率，同时有望拓宽其在跨高度、跨速度条件下稳定工作的能力，提高推进效率，有机动能力强、工作空域广、控制品质好等优点[2]。对于高超声速飞行器，通过使用大水平翼面对称气动布局时来实现高升阻比的同时，往往会给飞行器在主动段时的静不稳定状态下的姿态控制和在飞行末段的快速机动控制带来一定的设计困难，也难以满足不同发射条件下的尺寸约束。同时，很难实现全速域和大空域下的最优气动性能。

随着智能材料和结构等相关学科的发展，变形飞行器的相关研究已引起国内外学者的广泛关注。在现有研究中，大多数是以低速条件下的变形飞行器为对象进行研究，对应用于跨声速到超声速变形飞行器的相关研究相对较少。在美国国防部高级研究计划局(Defense Advanced Research Projects Agency， DARPA)开展的变形飞机结构(Morphing Aircraft Structures， MAS)项目中，按照合同要求，三家承包商分别进行了满足飞行器需求的变形方案设计，并在DARPA的资助下开展了相应的原型机开发和风洞试验，三家承包商分别采用了伸缩、变后掠以及三维折叠的变形模式来满足合同要求[3-5]。国外的Bae等[6-7]和国内的陈钱等[8]、郭建国等[9]、徐国武等[10]对伸缩变形飞行器以及变后掠、变前掠飞行器进行了气动和结构特性分析。张杰等[11]建立了变后掠及变展长组合变形飞行器的动力学模型，并进行了动态响应分析。在轨迹优化方面，陈功等[12]对不同飞行器的轨迹优化方法进行了详细的分析对比；黄国强等[13]综述了多飞行器协同轨迹优化和高超声速飞行器轨迹优化方面的相关进展，研究了轨迹优化数值算法。然而，关于变形飞行器轨迹优化的研究较少，并且其中大部分均集中于亚声速范围。其中，高飞云[14]、李焕焕[15]分别采用量子遗传算法和改进量子遗传算法针对适用于亚声速飞行的Z型折叠翼和伸缩变后掠翼变形飞行器的各段飞行轨迹进行了优化。

为了探索变形飞行器在高超声速环境下的应用模式，综合考虑射程及防热，针对分段式伸缩变形的翼身组合式飞行器的滑翔段进行轨迹优化。由于目标之间的冲突，本文采用多目标优化方法优化上述伸缩变形飞行器的滑翔弹道。目前，大部分多目标优化算法(包括广泛用于飞行器设计的改进的非劣分类遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ，NSGA-Ⅱ[16])主要使用种群进行多点搜索，并采用基于Pareto支配的适应度指定策略来获得近似的Pareto前沿。种种成熟的多目标优化算法在工程设计中均已有了成熟的使用案例，但是这些方法很难保持多目标优化问题的多样性，NSGA-II算法在选择过程中采取了拥挤距离机制，在通常情况下无法产生多个分布均匀的Pareto目标矢量，对于部分问题收敛速度也较慢。2007年，Zhang和Li提出了基于分解的多目标优化算法(Multi-objective Optimization Evolutionary Algorithm based on Decomposition，MOEA/D)[17]，它具有优化机制简单、收敛速度快、对Pareto前沿近似比较均匀的优点，近年来获得了广泛应用。MOEA/D将多目标优化问题转化为多个单目标优化子问题，并采用优化算法进行优化，然后这些子问题以合作的方式同时得到优化。

1 飞行器变形模式和气动特性

在飞行器变形中，翼面变形属于大尺度变形，因此对飞行器的气动特性和飞行控制有很大影响。目前采用的变形翼技术大多为翼面刚性变形方案[5]。变形模式主要包括伸缩翼、变后掠翼和折叠翼。三种变形模式广泛应用于低速及亚声速变形中。而在高超声速环境下，考虑到恶劣的力热环境以及高速环境下变形机构的可靠性，本文主要针对伸缩变形模式进行研究。

本文研究的飞行器基准外形为典型的面对称翼身组合式外形，如图1所示，具体外形情况见文献[18]。伸缩变形通过套筒结构实现，类似Raytheon公司设计的原理样机，如图2所示[3]。综合考虑飞行器发射约束及较为恶劣的飞行环境，为了增大飞行器在无动力滑翔段的射程，考虑采用二级伸缩的变形模式，从飞行器通过再入拉起进入滑翔段后，在高超声速阶段进行一次伸缩变形，当飞行速度下降到超音速时进行第二次变形。结合伸缩翼材料结构强度、头锥部脱体激波等因素的影响，设计得到基于基准外形的一级、二级伸缩变形外形如图3、图4所示。

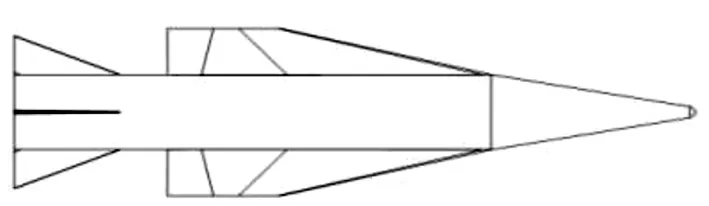
图1 基准外形示意图Fig.1 Base aerodynamic configuration

图2 Raytheon伸缩变形方案Fig.2 Raytheon′s telescopic wing morphing project

图3 一级伸缩外形Fig.3 The first stage of telescopic morphing wing aerodynamic configuration

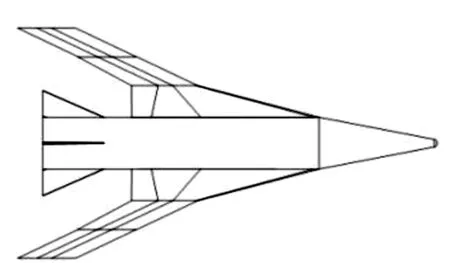
图4 二级伸缩外形Fig.4 The second stage of telescopic morphing wing aerodynamic configuration

为了节约篇幅，气动特性计算方法见文献[18]。针对基准外形在马赫数为6～8、一级伸缩外形在马赫数为3～8、二级伸缩外形在马赫数为2～6的工况下，对不同攻角的气动特性进行计算。由计算结果可知：伸缩翼变形飞行器在10°攻角附近升阻比最大；通过伸缩变形，飞行器最大升阻比提升明显，最大约增大10%。具体结果见图5～7。

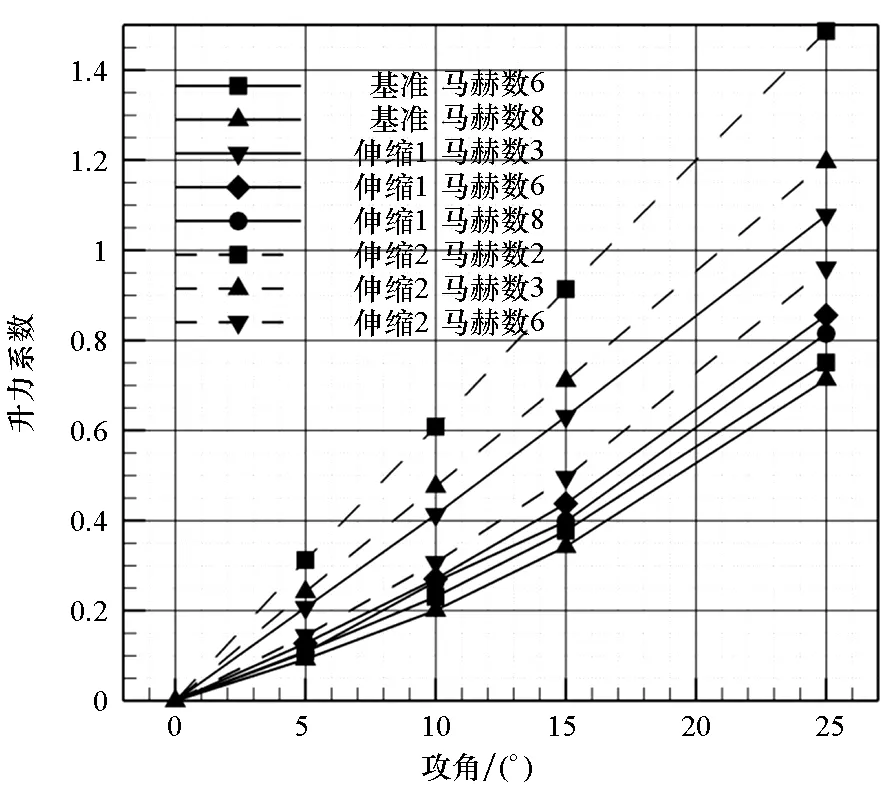
图5 不同外形升力系数随攻角变化Fig.5 Lift coefficient varying with attack angle

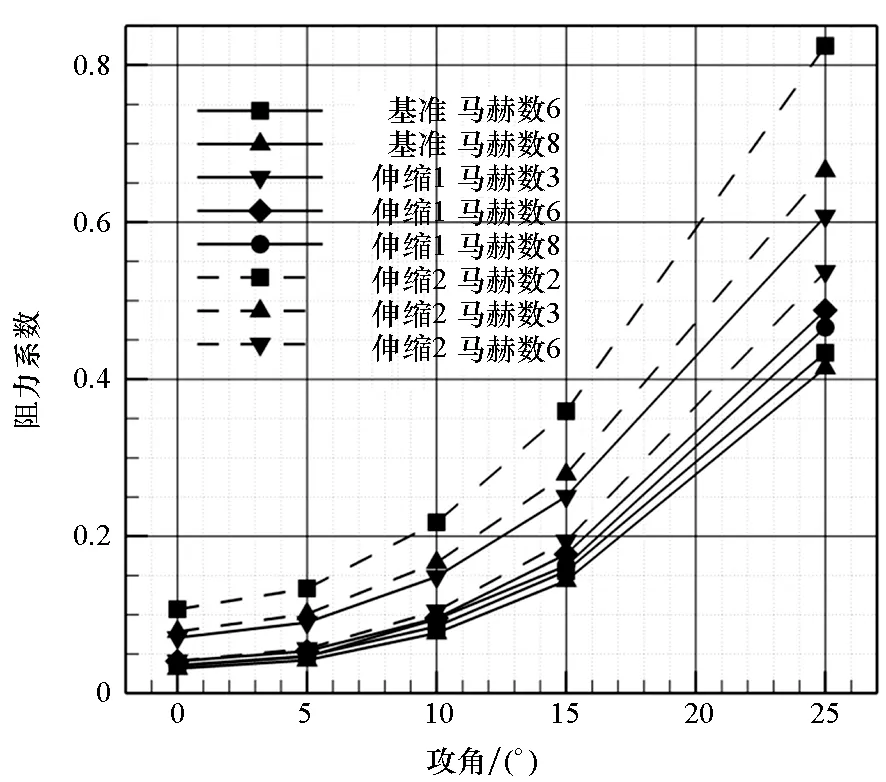
图6 不同外形阻力系数随攻角变化Fig.6 Drag coefficient varying with attack angle

图7 不同外形升阻比随攻角变化Fig.7 Lift to drag ratio varying with attack angle

2 弹道及热流计算模型

建立弹道模型时，假设地球为一旋转圆球，自转角速度ωm=7.292×10-5rad/s，且飞行器侧滑角为零，则在无动力滑翔状态下，建立得到变形飞行器三自由度运动模型，具体见文献[19]。

不同于一般飞行器主要对驻点处的热流进行估算，由于变形飞行器采用伸缩变形模式，变形伸缩翼前缘是拉起滑翔过程中受热最严重的部件之一，因此除头部驻点处以外，本文更多地需要考虑防热对变形机构可靠性的影响，在飞行过程中，通过对翼前缘热流的估算来确定整个过程中的翼前缘总吸热量，进而保证伸缩变形的顺利进行。

假设忽略弹身对伸缩翼的影响，伸缩变形翼前缘的热流可近似按后掠圆柱翼前缘热流公式计算[20]，即

qx=α(TwΛ-Tw)

(1)

式中，

TwΛ=Pr0.5(T∞0-TN0)+TN0

(2)

(3)

(4)

(5)

(6)

其中，Λ为后掠角。

由翼前缘总压pWSLΛ和恢复温度TwΛ通过热力学函数表得到密度ρwΛ。

当MaN∞≥1时，

(7)

当MaN∞<1时，

(8)

速度梯度du/dx由分段函数表示，当MaN0≥1.5时，

(9)

当0.8

(10)

其中，

(11)

由方程(1)～(11)，再结合Sutherland公式和气体状态方程，计算得到翼前缘热流，通过积分可得飞行过程中伸缩翼前缘的总吸热量Q。

3 变形飞行器轨迹多目标优化模型

在建立变形飞行器轨迹多目标优化模型时，需要对变形飞行器各方面的设计要求进行综合考虑，根据设计需求选择目标函数，在本文中主要是满足任务需求和飞行过程中的防热限制，同时考虑变形过程及飞行过程中的状态量，对设计变量进行确定。

3.1 目标函数

在确定优化问题时，目标函数的选择是其中一个关键环节。变形飞行器滑翔段轨迹优化的第一目标是使得滑翔段在满足下压条件的基础上尽可能地长，即在进入滑翔段之后使得变形飞行器尽可能处于最大升阻比状态，同时需要保证变形机构在高超声速及超声速恶劣的力热环境中的可靠性。

结合上文中的分析，选取滑翔段射程R和伸缩翼前缘总吸热量Q为目标函数。滑翔段射程越大，则表示变形对增大飞行器射程的效果越好；伸缩翼前缘总吸热量越小，则更有利于保护机翼内部变形机构不被破坏。

综上所述，确定变形飞行器滑翔段轨迹优化的多目标优化模型为

F=(maxf1=R，minf2=Q)

(12)

3.2 设计变量

针对一般的轨迹优化问题，主要是通过弹道参数的调整来完成对轨迹的优化，一般选取弹道参数中对优化目标影响较大的参数作为设计变量，比如攻角和速度倾角等。而对于变形飞行器轨迹优化问题来说，除弹道参数外，变形时机的选择也对飞行器轨迹有较大影响。因此在变形飞行器轨迹优化问题中，主要从变形时机和弹道参数两方面确定设计变量。

1)变形时机。变形飞行器采用二级伸缩变形模式，当飞行器进入无动力滑翔阶段时，随着马赫数降低，在合适的时机进行伸缩变形，以达到增大升阻比，进而增大滑翔段射程的目的。因此，选取两次变形的马赫数作为确定变形时机的设计变量。记当变形飞行器伸展一级伸缩机翼时的马赫数为M1；当变形飞行器伸展二级伸缩机翼时的马赫数为M2。

2)弹道参数。在本文研究的轨迹优化问题中，飞行器仅在纵向平面运动，而攻角α无论是对飞行升阻比还是伸缩翼前缘热流均有明显的影响，因此在轨迹优化模型中弹道参数主要考虑飞行过程中的攻角α。

由于变形飞行器采用二级伸缩变形模式，在无动力滑翔过程中，飞行器一共以三种不同的形态进行飞行，为了便于飞行控制实现，假设每种形态下飞行攻角均进行线性变化，三种形态下飞行攻角起点至终点依次用α1～α6表示。

综上所述，变形飞行器滑翔段轨迹优化模型的设计变量可表示为

x=(M1,M2,α1,α2,α3,α4,α5,α6)T

(13)

3.3 约束条件

针对本文的研究模型，约束条件主要由变形时机范围、弹道参数本身的取值范围和弹道约束条件组成。其中，变形马赫数的取值范围主要根据高超声速和超声速范围进行考虑，弹道设计参数约束条件主要根据飞行控制系统进行考虑，而滑翔段弹道终端约束则根据下压段速度、高度约束给出。

3.4 多目标优化算法

针对上节中建立的变形飞行器多目标轨迹优化模型，考虑射程和总吸热量两个目标函数中可能存在的冲突，本文采用MOEA/D优化算法对上述模型进行多目标优化计算。

MOEA/D基于传统聚合方法，将多目标优化问题(Multi-objective Optimization Problem，MOP)分解为多个单目标优化问题[21]。在MOEA/D中，根据权重矢量的距离来定义其相邻子问题，进而相邻子问题的优化信息可以共享。该算法大体包括初始化、更新和停止三个过程，为节省篇幅，本文不对算法进行详细描述，计算流程可参考文献[17]。

4 优化结果及分析

4.1 设计参数基准及指标

各外形气动参数见上节。取飞行器两次变形时的马赫数M1、M2为变形参数，三段轨迹攻角均为线性变化，由各段轨迹起始点及终点攻角确定。各参数基准值和取值范围如表1所示。滑翔拉起点参数如表2所示。

表1 设计变量

表2 拉起点参数

4.2 优化参数设计及结果分析

采用多目标进化算法MOEA/D对伸缩翼变形飞行器滑翔段轨迹进行多目标优化，分解方法采用Tchebycheff法，种群规模为200，迭代步数为300，邻居规模为20。

基于上节拉起点参数和设计变量基准值，由弹道和热流公式计算得到的变形飞行器基准方案滑翔段轨迹射程为760.25 km，伸缩翼前缘总吸热量为381.96 MW/m2。

优化结果的近似Pareto前沿如图8所示，MOEA/D采用Tchebycheff分解方法， Pareto前沿的两个端点分别对应本文两目标优化问题的两个单目标最优点。由图8可以看出，滑翔段轨迹射程最大与伸缩翼前缘总吸热量最小两个目标函数之间有明显的冲突。两个单目标最优方案的具体参数及目标函数值如表3中方案一、方案二所示，方案三为选定的折中多目标优化方案。

图8 变形飞行器多目标优化Pareto前沿Fig 8 Pareto front of multi-objective optimization for morphing aircraft

参数方案一方案二方案三M16.506.506.50M23.502.893.01α1/(°)14.999.1214.30α2/(°)159.5914.99α3/(°)159.2011.52α4/(°)159.059.43α5/(°)1511.3511.68α6/(°)158.288.17R/km765.40878.71844.07Q/(MW/m2)217.44344.39260.71

单目标最优方案有以下特点：

1)伸缩翼前缘总吸热量最小方案参数见表3方案一，在该方案中伸缩翼前缘总吸热量最小，相比基准方案降低约43.1%，射程基本保持不变，提高约0.7%。飞行弹道曲线如图9(a)所示，飞行时间约为517.9 s；

2)滑翔段轨迹射程最大方案参数如表3中方案二所示，在该方案中飞行器射程最大，相比基准方案提高约15.6%，伸缩翼前缘总吸热量降低约9.8%。飞行弹道曲线如图9(b)所示。

将单目标最优方案与基准方案性能进行对比，可以得知，两种方案的伸缩翼前缘总吸热量均有明显降低，这是由于两种方案下弹道飞行相较基准方案更为平稳，且飞行高度更高，因而在飞行环境下密度压力更小，使得热流更低。

选定的多目标优化方案和基准方案的高度-射程曲线如图9(c)、图9(d)所示，选定的多目标优化方案与基准方案相比，射程提高约11%，伸缩翼前缘总吸热量降低约31.7%。与单目标最优方案进行对比，飞行器射程与射程最大方案相比减小约3.9%，伸缩翼前缘总吸热量与总吸热量最小方案相比增加约19.9%。由上述分析可知，选定的基准方案并不在Pareto前沿上，具备改进空间。同时，选定的多目标优化方案是在两目标函数中进行权衡折中的结果，在射程最大方案的基础上，牺牲了3.9%的射程，使得伸缩翼前缘总吸热量约减小了24.3%。

(a) 方案一(a) Scheme 1 (b) 方案二(b) Scheme 2

(c) 方案三(c) Scheme 3 (d) 基准方案(d) Baseline scheme图9 不同方案高度-射程曲线Fig.9 Altitude-range graph of different solutions

为了验证采用伸缩变形方案的效果，采用与表3中三种优化方案相同的攻角指令，对未变形的翼身组合式飞行器进行轨迹仿真，并将文中确定的目标函数值进行对比。上文中三种优化方案参数下的目标函数值以及采用伸缩变形方案后的目标函数增量见表4。表中R和Q代表未变形的飞行器滑翔段轨迹射程和伸缩翼前缘总吸热量值，MorphR和MorphQ代表采用了变形技术后飞行器滑翔段轨迹射程和伸缩翼前缘总吸热量的变化幅度。

表4 原始外形不同方案下目标函数与变形方案对比

通过对三种优化方案分别采用原始外形和伸缩变形得到的目标函数值进行对比分析可知：采用伸缩翼变形方案与无变形外形相比，可以增大滑翔段轨迹射程，并减小伸缩翼前缘总吸热量，相比单目标优化方案，在选定的折中多目标优化方案中，伸缩变形翼对目标函数的改善更为显著。上述分析表明，通过采用伸缩翼技术增加了飞行器的升阻比，使得飞行器的滑翔段轨迹射程得到了一定幅度的增加，同时高升阻比外形使得变形飞行器的滑翔弹道高度高于原飞行器的滑翔弹道，更小的大气密度和压强使得翼前缘总吸热量明显减小，从而进一步保证了变形机构的可靠性。

5 结论

为进一步探索变形技术在高超声速条件下的应用前景，本文将伸缩翼变形技术与翼身组合式外形相结合，介绍了一种适用于高超声速的二级伸缩翼变形飞行器。通过将变形时机和弹道相结合，基于MOEA/D提出了一种适用于变形飞行器的滑翔弹道多目标优化设计方法。选取滑翔段射程和伸缩翼前缘总吸热量作为优化的目标函数。优化结果表明，所提出的优化方法切实可行，可以得到满足任务需求的最优解，所选取的目标函数具有较强的冲突性，优化方案是两者折中权衡的结果。下一步可以考虑结合弹道情况建立更多目标函数或约束。

与未变形外形相比，在单目标及多目标优化最优方案中，采用伸缩翼变形技术使得目标函数均有一定程度的改善，其中又以选定的折中多目标最优方案情况改善最为明显，通过变形，飞行器滑翔段射程约增加了8.52%，伸缩翼前缘总吸热量约减小了9.61%。