机翼变形的临近空间太阳能飞行器平稳升空方案*

郭天豪，侯中喜，王 鹏，高 俊

(国防科技大学 空天科学学院， 湖南 长沙 410073)

临近空间太阳能飞行器由于可以实现海拔20 km以上区域持久驻留，被作为理想的通信中继和侦查平台得到了广泛的发展[1-2]。现阶段临近空间太阳能飞行器设计的瓶颈问题是昼夜能源闭环，尤其是夜间的能源平衡[3]。由于临近空间大气密度稀薄，太阳能飞行器在高空实现升重平衡所需的飞行速度远大于低空飞行速度，而平飞功率与飞行速度的立方成正比[4]。因此，为了降低飞行器在高空的飞行速度，临近空间太阳能飞行器往往采用高升阻比翼型和大展弦比轻质布局[5]。由于临近空间位于平流层，大气条件平稳，这样的布局非常符合临近空间工作点的各方面需求。然而在低空，由于湍流的影响且飞行器速度过低，飞行安全性受到了显著的挑战[6]。美国太阳神原型机HP-03在一次升空试验中，受气流干扰后空速与俯仰角发生耦合振荡，逐渐发散后最终坠毁[7]。分析显示纵向稳定性和操纵性均不足是造成这次事故的重要原因[8]。

可变形飞行器是指可以通过大幅改变气动外形，从而较好地适应不同环境和任务性能的航空器[9-10]。通过改变自身的展长、后掠、上反角等结构布局或者改变翼型[11]，飞行器可以实现不同环境、不同飞行阶段的最佳综合性能[12]，并可以拓展飞行包线。

为了实现太阳能飞行器临近空间工作点与低空起飞点的匹配，本文提出了基于主动变形的飞行器升空方案。针对性地建立了可变形飞行器的气动模型和推力模型，进行了不同飞行器构型俯仰、滚转和偏航三个通道稳定性和操纵性的定量分析。最后优化给出了从地面到高空机翼逐渐展平的升空方案，并对升空过程中各高度所需平飞推力和功率进行了校核。

1 多段可变形飞行器初步方案

针对临近空间太阳能飞行器在中低空由于速度低、自身稳定性差等引起的飞行安全性问题，本文将飞行器主动变形作为一个方案进行分析和验证，以给出飞行器从地面升空过程中的安全飞行方案。

本文以飞翼式布局的第三代太阳神原型机，即HP-03作为参考，提出可主动变形的多段式太阳能飞行器方案，如图1所示，在HP-03的基础上，将其主机翼分成等长度的三段，各段之间通过转轴连接可以进行主动折叠变形。因而，飞行器的构型可以随着两翼折叠角发生变化。

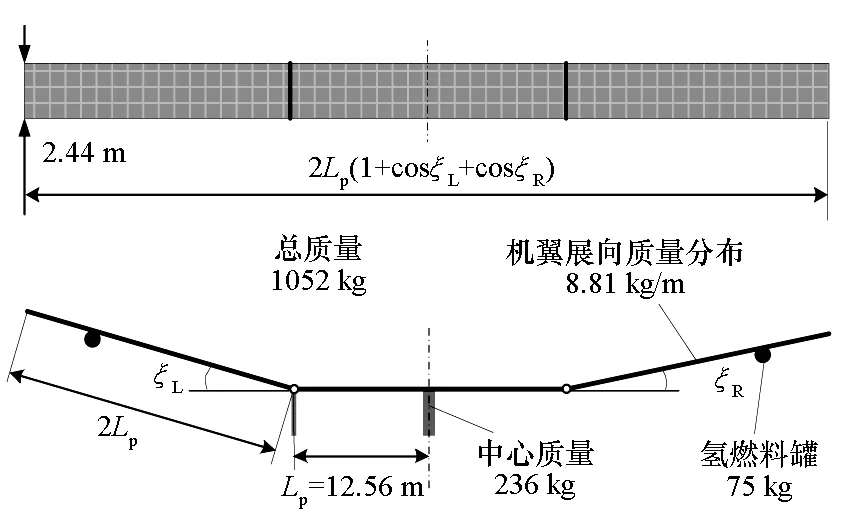
图1 分段式可变形飞行器结构示意图Fig.1 Sketch of segmented morphing aircraft

在进行建模与分析时，认为飞行器主机翼结构质量沿翼展方向均匀分布，而将中心的载荷吊舱和两侧的氢燃料罐作为集中质量点进行简化。氢燃料罐到翼稍的距离为1/4单段展长。飞行器主要结构分布参数如表1所示。

表1 飞行器主要结构参数

多段可变形飞行器各段的翼展只有太阳神HP-03翼展的1/3，受扰后结构柔性变形会显著降低。且近年来临近空间太阳能飞行器的结构刚度有了明显的提升。因此，在随后的分析中，忽略飞行器各翼段柔性变形的影响，只考虑受控的刚性主动变形。

2 多段飞行器力矩建模方法

飞行器的稳定性与操纵性主要与力矩平衡与控制相关，因而准确的力矩建模是研究飞行器安全性的关键。

2.1 气动系数简化建模方法

与常规飞行器相比，可变形飞行器受到扰动后，其气动系数不仅会受到气流角、飞行状态的影响，还会受到变形的影响。气动软件只能在离散的有限构型上计算飞行器气动数据。为了能够更加深刻地阐述气动系数随飞行器变形连续变化的机理，本文采用简化的气动模型来推导气动力及气动力矩的表达式。

考虑到气动计算时，侧向的气动力和力矩不仅与机翼水平投影面积有关，而且与机翼竖直投影面积有关。将参考量设置为各段累加值，而非飞行器机体横轴的投影值，即参考展长和参考面积为

(1)

飞行器在完全展平时，由于在设计上具有静稳定性，主机翼压心在质心之后，约1/4弦线的位置处，在飞行器折叠变形的过程中，各面元上所受的气动力在x轴方向上也不发生变化，因而压心的x轴方向坐标为固定值，即

xcp=-0.25cA=-0.61 m

(2)

位于固定段、左翼段或右翼段上，距离接转轴距离为l的面元dS在浮动机体系中的坐标分别为：

(3)

式中，ξL和ξR分别为左侧和右侧可变形段的折叠角。注意到除翼稍处的面元外，其余单个面元在其自身稳定轴系中并不产生侧力。且由于飞行器具有很大的展弦比，故而可以忽略翼稍处的微小侧力。考虑到迎角α在面元体轴系中，单位气动力为

(4)

2.1.1 固定段上的气动系数

在小迎角、小侧滑时，飞行器气流角近似有以下关系式

(5)

式中，Vx,Vy,Vz空速矢量在机体系各坐标轴上的分量。固定段上的迎角与侧滑角等同于整机的迎角与侧滑角。因此，其升力系数为

(6)

式中，CLa为翼型的升力线斜率。在迎角变化较小时阻力系数可以认为几乎不变，即认为CD为常数。

因此，固定段产生的总升力为

(7)

固定段总气动力矩为

(8)

其中，

(9)

机翼固定段由于关于中心平面对称，所产生的侧力、滚转力矩和偏航力矩均为零。

2.1.2 可变形段上的气动系数

如图2所示，对于左翼段上、右翼段的面元dS，其切向速度仍为Vx，垂直于面元的法向速度变为

(10)

图2 可变形段面元法向速度示意图Fig.2 Normal velocity on foldable wing segments

因而，两侧可变形段的实际迎角变为

(11)

因此，左翼段、右翼段上面元的升力系数将与固定段上的不同，即为

(12)

各可变形段产生的总升力为

(13)

并产生相应的侧力为

(14)

将飞行器机翼各面元上的气动力投影在机体系各坐标轴中，同时以面元位置叉乘，可以得到面元对整机三维气动力矩的贡献，进一步积分可得

(15)

其中，各轴力矩系数的详细表达式为

(16)

2.1.3 整机气动系数与验证

基于以上分析，整机升力系数为

(17)

变形引起的整机侧力系数为

(18)

而整机气动力矩系数，则是将以上各段产生的气动力矩系数直接相加。

为验证本文所提快速气动建模方法，选取两个特征构型，分别采用本文方法和AVL软件计算其气动参数，其对比结果见表2。

由表2可知，本文所采用的简化算法与AVL计算所得的气动力系数非常接近，而在计算力矩时有一定误差，但能很好地反映气动参数随构型的变化趋势。

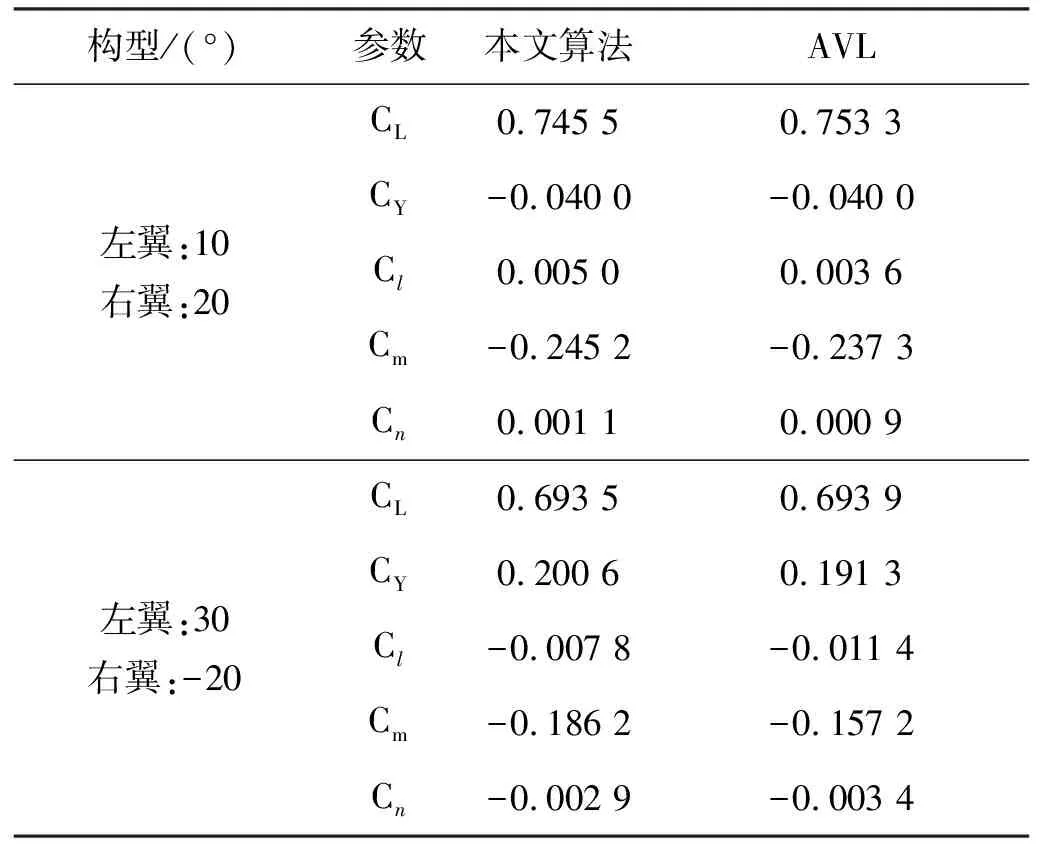
表2 快速气动建模方法验证

2.2 推力及其力矩的建模

参照HP-03的螺旋桨分布，飞行器有10个螺旋桨且成对分布。在固定段上有1对螺旋桨，其与固定段几何中心的展向距离为LT0，在可变形段上有4对螺旋桨，其与折叠转轴的展向距离为LTi。 旋桨展向分布间距参数为

(19)

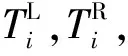
(20)

对于固定段上的一对螺旋桨而言，如果两侧推力不对称，则其产生的推力产生偏航力矩为

(21)

对于两侧翼段上的每对螺旋桨，其产生的推力力矩为

(22)

3 飞行器不同构型稳定性分析

稳定性是指飞行器受到扰动后，其姿态是否拥有恢复受扰前状态的能力。足够的稳定性是飞行器安全飞行的首要保障。稳定性分析的基点是飞行器的平衡状态，而飞行器在平衡状态时通常应具有对称构型，即两侧变形角相等。

3.1 纵向静稳定性

飞行器纵向静稳定性通常用俯仰力矩系数对迎角的导数，即Cma来衡量，为负时飞行器静稳定，因为此时飞行器迎角扰动后飞行器会产生相应的俯仰恢复力矩。如图3所示，将不同构型俯仰力矩对迎角求导，可得Cma随构型变化关系。

由图3可以看出，当飞行器两翼由展平状态上折时，飞行器纵向静稳定导数保持负值并降低，这表明飞行器纵向静稳定性随变形角增大而增强，且在变形角位于42°附近达到极值。当变形角位于20°至60°时，飞行器纵向静稳定性始终位于较高水平。

图3 飞行器纵向静稳定导数Fig.3 Longitudinal static stability derivative

3.2 横向静稳定性

飞行器横向静稳定性通常用滚转力矩系数对侧滑角的导数，即Clb来衡量，为负时飞行器静稳定，因为此时飞行器发生侧滑后，飞行器会向反方向倾斜，从而升力会产生反方向的水平分量来抑制飞行器的侧滑。如图4所示，将不同构型滚转力矩对侧滑角求导，可得Clb随构型的变化关系。

图4 飞行器横向静稳定导数Fig.4 Lateral static stability derivative

由图4可以看出，当飞行器完全展平时，横向静稳定导数为零，此时飞行器是中立稳定的。随着飞行器两侧机翼的上折，飞行器横向静稳定性逐渐增强；随着飞行器两侧机翼的下折，飞行器横向静稳定性逐渐减弱。与之类似，常规固定翼飞行器通常会使机翼两端上反以提高飞行器横向静稳定性。

3.3 航向静稳定性

飞行器航向静稳定性通常用偏航力矩系数对侧滑角的导数，即Cnb来衡量。航向静稳定导数为正时飞行器静稳定，因为当飞行器往一侧发生侧滑时，正的航向静稳定导数将使飞行器产生向侧滑同侧偏转的力矩，使得飞行器的机头偏向侧滑方向，从而减小侧滑。如图5所示，将不同构型偏航力矩对侧滑角求导，可得Cnb随构型的变化关系。

由图5可以看出，在飞行器完全展平时，航向静稳定导数约为0.5，此时飞行器是静稳定的。而随着飞行器两侧机翼的上折，航向静稳定导数减小直至变为负值，飞行器逐渐静不稳定。飞行器迎角越大，航向静稳定导数随构型变化得越剧烈。取飞行器迎角为设计状态6°，当飞行器两侧上反角大于16°时，航向开始静不稳定，航向静稳定导数在上反角50°时取得极小值-0.05，随后开始缓慢回升。

图5 飞行器航向静稳定导数Fig.5 Directional static stability derivative

需要说明的是，在大上反角时，飞行器航向虽然静不稳定，但是Cnb的绝对值是很小的，即静不稳定是轻度的，航向受扰时会很缓慢地发散。此外，飞行器具有非常大的展长和沿展向分布的电动推进系统，因而具有很强的航向姿态控制能力，当航向轻度静不稳定时是可以保证平稳飞行的。

4 飞行器不同构型操纵性分析

飞行器的变形显著改变了飞行器所受到的气动力和气动力矩，因而也为飞行器提供了额外的控制通道。但受到惯性、气动载荷、结构和材料强度等各方面的限制，所允许的飞行器变形必然是缓慢的。

临近空间太阳能飞行器的姿态运动往往具有幅度小、频率高的特征，采用缓慢的变形来控制姿态是难以实现稳定的。因而为了稳定并控制飞行器的姿态，用于控制俯仰的升降舵和用于控制滚转的副翼仍然是必要的，而偏航姿态可以利用分布于主机翼上的推进系统的差动来实现控制。在此前提下，飞行器的操纵性主要由舵面和推进系统来提供。

4.1 舵面操纵性

由于飞行器的升降舵位于主机翼固定段，因而在不考虑三维效应时，可以认为俯仰操纵性导数Cmde并不随飞行器构型发生变化。而两翼升力系数由于实际迎角的减小会减小，且副翼到机体系中心的力臂也会减小，因而随着变形角绝对值的增大，滚转操纵性导数Clda的绝对值会减小。

假设飞行器最大舵偏角为45°，根据不同构型对应的全机动压，可以得出舵面可产生的操纵力矩如图6所示，注意纵轴为对数坐标。

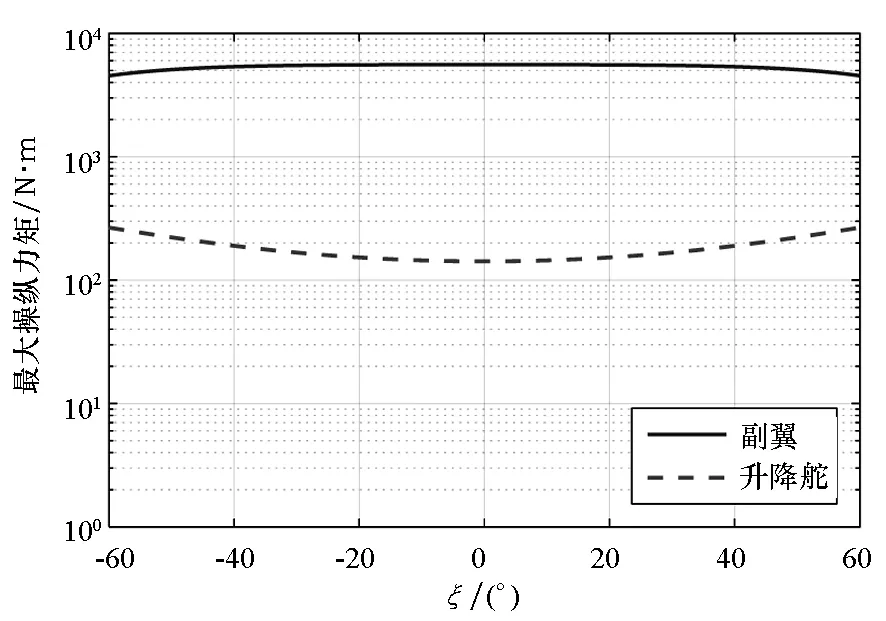
图6 舵面最大操纵力矩Fig.6 Maximum control moment produced by flaps

图6展示了舵面可产生的操纵力矩范围。可以看出，随着飞行器变形角绝对值的增大，副翼能产生的滚转操纵力矩有所变小。这是由于一方面变形导致滚转操纵性导数Clda的绝对值减小；另一方面配平时动压增大，气动操纵能力提升。因此，飞行器折叠后，虽然最大滚转操纵力矩有所减小，但变化幅度并不剧烈。而随着飞行器变形角绝对值的增大，升降舵能产生的俯仰操纵力矩变大，这是由于随着变形角绝对值的增大，飞行器升力系数减小，飞行速度增大，因而动压增大，气动操纵能力提升。

通过图6还可以看出，即使在机翼大幅折叠的情形下，滚转操纵力矩也要大俯仰操纵力矩一个数量级以上。因而对于多段飞行器，增强其俯仰操纵能力更为迫切。

4.2 推进系统附加的操纵性

定义飞行器横向、竖向推力配置参数τy,τx∈[-1, 1]，各螺旋桨推力按如下控制率进行分配：

(23)

(24)

根据推进系统模型式(22)，在飞行器对称变形时，推力分配所产生的俯仰力矩为

(25)

飞行器以各螺旋桨推力相等进行配平，因而配平时推力提供的俯仰力矩为

(26)

式(25)和式(26)相减，再将控制分配律式(23)代入，可得推进系统俯仰操纵力矩为

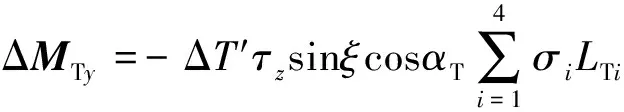
(27)

进一步将推进系统位置分布式(19)代入，可得纵向操纵力矩为

(28)

注意到，ΔT′与配平推力、最大允许推力相关，而二者都受飞行器配平速度的影响，因而也受到飞行器构型与海拔高度的影响。

用同样的方法，可以得出横向操纵力矩为

(29)

对比式(28)与式(29)可知，本文所提的推进系统控制分配律，俯仰控制与偏航控制是相互独立的，即横向推力配置参数τy只影响偏航操纵，竖向推力配置参数τz只影响俯仰操纵。

如图7所示，不同海拔高度下，由于配平推力不同，推力最大允许差量ΔT′相差很大，因此推力可提供的最大操纵力矩差别也很大。然而在低空，飞行器折叠后通过推进系统差动方案式(23)可以提供的俯仰力矩和偏航力矩都是非常可观的。因此，推力差动可以有效地应对飞行器低空俯仰操纵能力不足的问题。

图7 推进系统最大操纵力矩Fig.7 Control moment produced by flaps

5 飞行器平稳升空方案

由第3节与第4节的分析可知，随着变形角的增大，飞行器配平时的稳定性和操纵性都有显著的提升。付出的代价是飞行速度提升后，所需的平飞能耗增大。本节旨在通过建立不同飞行器不同高度的优化目标与约束条件，然后选取优化算法，得出不同高度下飞行器安全飞行的最优构型。

5.1 基本方案

飞行器的静稳定性由滚转、俯仰、偏航三个静稳定性导数共同决定。对于飞行而言，可接受的最大迎角、侧滑角扰动为αmax,βmax，则静稳定指标可以用

ψstab=[-Clbβmax, -Cmaαmax,Cnbβmax]T

(30)

即最大扰动引起的恢复力矩系数进行表征，各分量越大，表明相应通道的稳定性越强。

飞行器的操纵性由舵面操纵性和推进系统操纵性共同组成，也分为滚转、俯仰、偏航三个通道。为了形成统一的优化指标，定义归一化的操纵性向量为

(31)

其中，Q为飞行器动压，因此ψctrl的物理意义为各通道操纵所对应的最大力矩系数，各分量越大，表明该通道操纵性越强。

飞行器另一重要指标是爬升功耗。定义归一化的爬升功耗为飞行器的爬升功率与最大可用功率之比，即

(32)

此外，飞行器在不同高度受到的气流扰动也不同，将飞行器受到最大允许垂直突风时所引起的迎角扰动作为归一化的受扰指标，即为

(33)

在飞行过程中，通常期望稳定性与操纵性尽可能强，而功耗与扰动尽可能小。因此，优化目标函数为以上各指标的加权

J=w1ψpow+w2ψdist-w3ψstab-w4ψctrl

(34)

其中，w1,w2,w3,w4分别功耗指标、受扰指标、稳定性指标、操纵性指标的权重系数。因此，对于每一高度，该优化问题可表述为

(35)

在算例中，取αmax=8°,βmax=15°，ψss=[-0.02, 0.2, -0.02]T，Vwmax=4 m/s。

当海拔高度低于10 km时，飞行器位于对流层，此时外界大气紊流显著，因而要提高受扰指标的相对权重，同时增加稳定性指标的权重；当海拔高度位于10～20 km之间时，飞行器位于平流层，此时外界大气环境平稳。为了实现高空长航时飞行，需要降低受扰指标的权重与稳定性指标以降低飞行速度。而且随着海拔高度的提升，能源平衡越来越苛刻，因而能耗的权重应该增大。因此，设置各待优化指标的权重系数为以下随海拔变化的函数：

(36)

在各高度，构型优化结果如图8所示。

图8 不同高度最优构型Fig.8 Optimized configuration in each altitude

从优化结果可以看出，飞行器在低空时，采用较大的折叠角进行爬升，而在爬升至20 km的过程中主机翼逐渐展平。飞行器在达到20 km后依然保持小角度的上反，相对于完全展平升力虽然有损失，但损失非常微弱。

5.2 操稳特性校核

按照以上升空方案，飞行器在由地面到临近空间的升空过程中的操稳特性增量如图9所示。即为操纵性指标与稳定性指标的增量。

(a) 操纵性(a) Controllability (b) 稳定性(b) Stability图9 飞行器升空过程操稳特性增量Fig.9 Stability and controllability in climbing process

通过图9可以看出，采用基于变形的飞行器升空方案之后，在中低空飞行器滚转操纵性略有降低，而稳定性显著增强；俯仰操纵性和稳定性都有大幅提升；偏航稳定性和操纵性略有下降。

5.3 能耗校核

基于优化的升空过程中构型方案，飞行器在不同海拔高度的平飞需用推力和平飞需用功率如图10所示。

(a) 推力(a) Thrust (b) 功率(b) Power图10 飞行器不同海拔平飞推力和功率Fig.10 Level flight thrust and power in different altitude

由图10可见，采用变形方案来解决飞行器在中低空的安全性时，推力变化很小，而由于速度的增加，飞行器在中低空平飞所需的功率会大于不变形时相应的值。然而平飞功率始终不大于设计工况，即20 km时的功率，因而该方案不会提出额外的能源需求。

6 结论

为了解决临近空间太阳能飞行器在低空的安全性问题，本文针对性地建立了可变形飞行器的气动模型和推力模型，在此基础上进行不同飞行器构型俯仰、滚转和偏航三个通道稳定性和操纵性的定量分析。最后给出了从地面到高空机翼逐渐展平的升空方案，并对升空过程中各高度所需平飞推力和功率进行了校核。得出以下结论：

1)在±40°范围内，随着飞行器变形角的增大，配平时俯仰、滚转静稳定性增强。

2)随着飞行器变形角增大，飞行器俯仰操纵能力显著提升。

本文提出的方案和相应的分析方法对于飞行器应对低空湍流问题具有一定的参考意义。