吸气式高超声速飞行器助推分离过程数值仿真*

闻 讯,柳 军,夏智勋

(国防科技大学 空天科学学院, 湖南 长沙 410073)

吸气式高超声速飞行器是典型的高动态临近空间飞行器，具有飞行速度快、机动性能好等优点[1-3]，是近年来国际军事研究热点，其相关研究已列入多国战略技术部署计划[4-5]。为了达到启动条件，吸气式高超声速飞行器必须借助运载器提速，并在指定弹道高度实现助推分离，助推分离过程属于典型的多体分离问题[6-9]。

针对多体分离问题，目前已开展多项相关研究并取得了一定进展。张海瑞等[10]采用重叠网格技术对子母弹分离过程进行了数值研究，研究发现，满足俯仰角速度分离指标比满足俯仰角条件更苛刻。Chamberlain等[11]对整流罩分离问题进行了高精度数值仿真研究，研究发现，在抛罩分离指令下达后的一段时间内，罩体的尾流区域仍影响后体的流场分布。多体分离过程通常存在多体干扰问题[12-15]，王元靖等[16]在超声速多体分离实验中发现载荷模型的气动特性受分离位置的影响而变化显著。Togashi 等[17]采用非结构网格对投弹问题进行了数值仿真研究，得到了分离过程中清晰的激波干扰图像，且与风洞纹影实验结果吻合。Li等[18]通过改变分离条件对火箭转级过程进行了研究，得到不同分离距离下的级间区流场分布差异。然而，关于多体分离问题的快速非定常数值计算方面的研究较少，尤其针对前体飞行器通流快速非定常数值计算的研究，对其分离规律和机理仍没有明确的结论。

随着网格构建技术的逐渐发展，多种网格模型可应用于多体分离问题的求解，主要包括整体网格变形技术、动网格技术、局部网格重构技术以及嵌套网格技术等[19]。这使得复杂构型飞行器的非定常数值研究成为可能。

本文针对带圆顶泄流以及减速板布局的试飞器构型，采用非结构网格下的局部网格重构技术，提出适用于求解复杂构型多体分离问题的六自由度非定常方法。并采用重叠网格技术加快收敛，对该构型在四组弱干扰冷态分离条件下进行数值仿真，得到试飞器在不同分离条件下的流场布局和气动特性。通过对仿真结果的分析得到最优来流分离条件。

1 物理模型

1.1 几何模型

带级间泄流结构以及减速板构造的转级阶段试飞器气动模型如图1所示，该试飞器主要由吸气式高超声速飞行器、级间段和助推器三部分组成，气动模型总长约8 m。飞行器采用头部进气、多模块进气道以及中心燃烧的固体冲压式发动机构型，尾部共有四片舵面和导流块，呈“×”字布局。级间段采用圆顶泄流结构，助推器主体为直径0.6 m圆柱结构，沿助推器左右两侧对称布置四片减速板(见图2)，全部张开时相对于飞行器纵向对称面呈迎风70°，助推器尾部共有四片尾翼，呈“×”字布局，翼展约2 m。

图1 试飞器气动外形图Fig.1 Vehicle geometric shape

图2 分离组件局部放大图Fig.2 Enlargement of separation components

1.2 基准网格

计算所使用的基准网格是借助ICEM软件生成的，根据分离模型特点对气动模型表面做了适当加密。生成模型的表面网格后，采用八叉树方法生成计算域的体网格，并进行网格质量优化。最终生成四面体网格规模约为112万，多重网格层数为5。图3和图4分别给出了气动模型纵向对称面网格和体轴水平截面网格示意图。

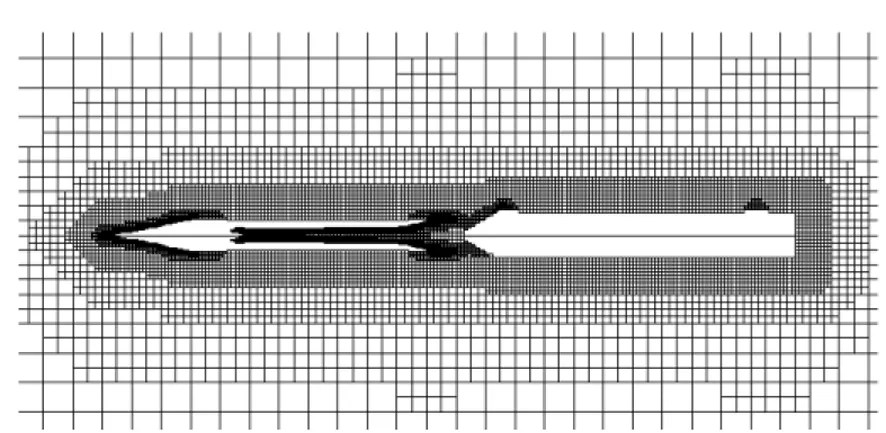
图3 网格外形纵向对称面网格Fig.3 Grid profile on the longitudinal symmetrical surface

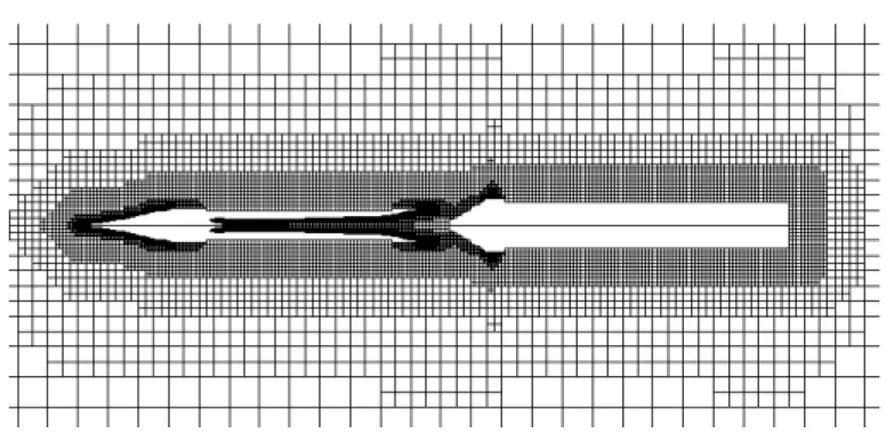
图4 网格外形体轴水平截面网格Fig.4 Grid profile on the horizontal center surface

2 数值方法及分离条件

2.1 六自由度运动方程及求解

建立与前体固连的惯性坐标系和与后体(分离刚体)固连的本体坐标系。在惯性坐标系中求解有运动边界条件的流动问题，三维N-S 方程如式(1)所示。

(1)

式中：Q为守恒变量；Fc为无黏通量；Fv为黏性通量；xc为网格移动速度。

本体坐标系下，针对分离刚体可以得到式(2)～(4)。

(2)

(3)

(4)

其中：M为外力对刚体质心的合力矩；I为刚体惯性矩张量；ωx，ωy，ωz分别为刚体的角速度ω在本体坐标系下三个方向的分量；φ为滚转角；θ为俯仰角；φ为偏航角。

2.2 分离条件

非定常六自由度计算的初始条件是通过定常计算得到的，数值模拟的来流条件为：马赫数4.3，高度14 km，助推器分离的初始角速度和初始线速度均为零，其他初始参数见表1。

表1 助推器分离初始参数

基于上述基础工况再参考不同来流攻角和侧滑角条件设计四组算例，用于考察来流条件波动对安全分离结果的判断和影响，算例条件及编号说明在表2 中给出。

采用四核2.67 GHz主频、12 GB内存的 Inter Core i7 CPU 920处理器开展本算例的非定常计算工作，完成每个时间状态点的循环迭代计算约需要6.5 h，若取用30 ms作为非定常计算的时间间隔，则完成300 ms的单状态计算周期为3 d。

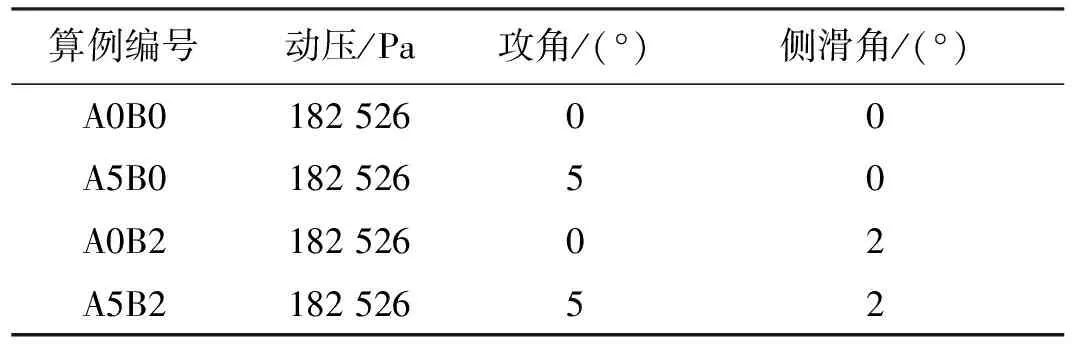
表2 算例来流参数说明

3 结果与讨论

采用非定常的计算方法得到试飞器在四种分离条件下飞行器YZJ和助推器ZTQ的气动阻力和分离速度，定义分离力Δ为ZTQ和YZJ两者阻力的差值，并将其作为一项分离指标，Δ为正值时即可实现分离。另外，定义分离加速度比Rat为YZJ加速度比与ZTQ加速度的商值，不大于1的分离加速度比被认为对分离有利。

3.1 分离过程

图5给出了各算例在分离过程中的机体阻力及气动分离力，图6给出了各算例在分离过程中的分离加速度及分离加速度比。其中，带攻角状态结果用实心符号表示、带侧滑角状态结果用实线表示。由图5可见，在分离过程中YZJ气动阻力在分离初始时刻稍有波动，约在100 ms以后流场稳定，阻力基本不再变化。从状态对比的数值上看，A5B0和A5B2状态阻力较A0B2和A0B0状态阻力略大。分离力曲线变化趋势主要受ZTQ阻力发展规律影响，总体上先稍有减小后迅速增大，且带攻角状态的增长趋势更强。不难发现，图6中的加速度与图5中的阻力之间存在正比例关系。另外从图6中右侧坐标值所对应的分离加速度比数值来看，分离加速度比在整个分离过程中均保持在安全值0.8以内，无攻角状态最大值不超过0.2，其余状态最大值约0.3，满足安全分离需求。

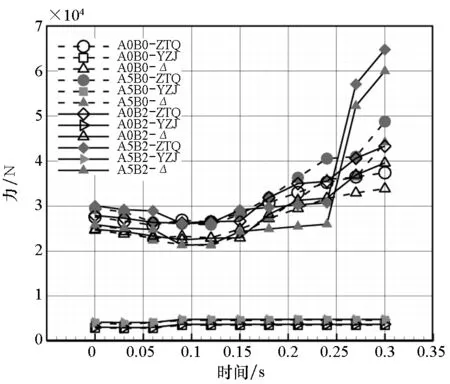
图5 机体阻力及气动分离力对比曲线Fig.5 Comparison curve of body forces and aerodynamic separation forces

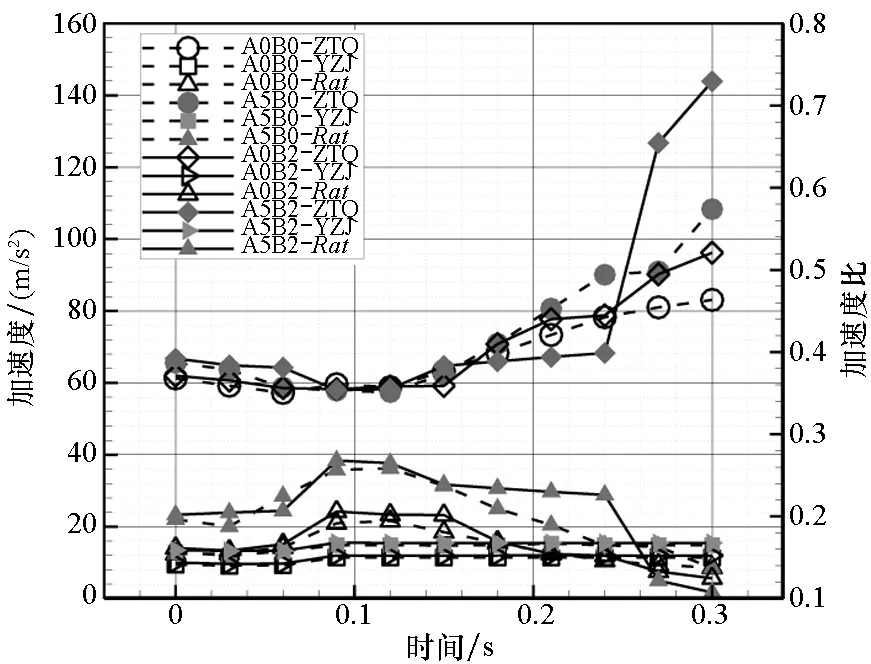
图6 分离加速度及分离加速度比对比曲线Fig.6 Comparative curve of separating acceleration and separating acceleration ratio

助推器线速度分布如图7所示，助推器角速度分布如图8所示。由图7线速度变化曲线可知，X方向分离运动最为明显，随时间发展近似呈二次曲线变化规律，助推器分离运动由快至慢的工况顺序依次是A5B2、A5B0、A0B2、A0B0。分析最佳分离来流条件，除了分离速度可作为一个参考指标以外，分离的安全性、稳定性、可靠性都很重要，本文从角速度以及周向线速度的角度来考核后三项重要指标。从Y方向的线速度结果分析来看，无攻角对应两组工况的助推器分离线速度更小，即认为工况A0B0和A0B2的Y方向分离更满足上述指标；而在Z方向无侧滑角对应的两组工况在Z方向的线速度基本为零，假设控制系统完善，鉴于安全分离的考虑，工况A0B2是更合适的选择。由图8角速度分离曲线可知，A0B0和A5B0状态Y方向角速度基本为零，Z方向角速度相对很小，可认为其对应翻转运动较弱。A5B2和A5B0在X方向运动最为明显，Y方向运动和Z方向运动对应最明显的状态是A0B2和A5B2，且角速度增长较快，伴随有非常明显的滚转运动；同时，分离过程中A5B2状态助推器的滚转运动较A5B0和A0B2更为明显，A0B2其次，A0B0状态飞行器滚转效应最弱。

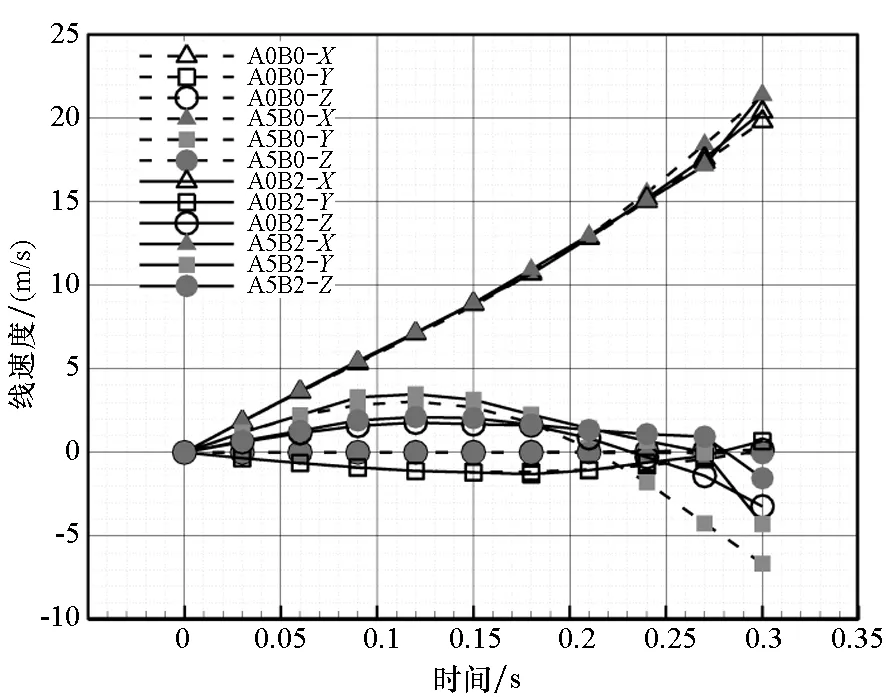
图7 助推器线速度分布Fig.7 Line velocity distribution for booster

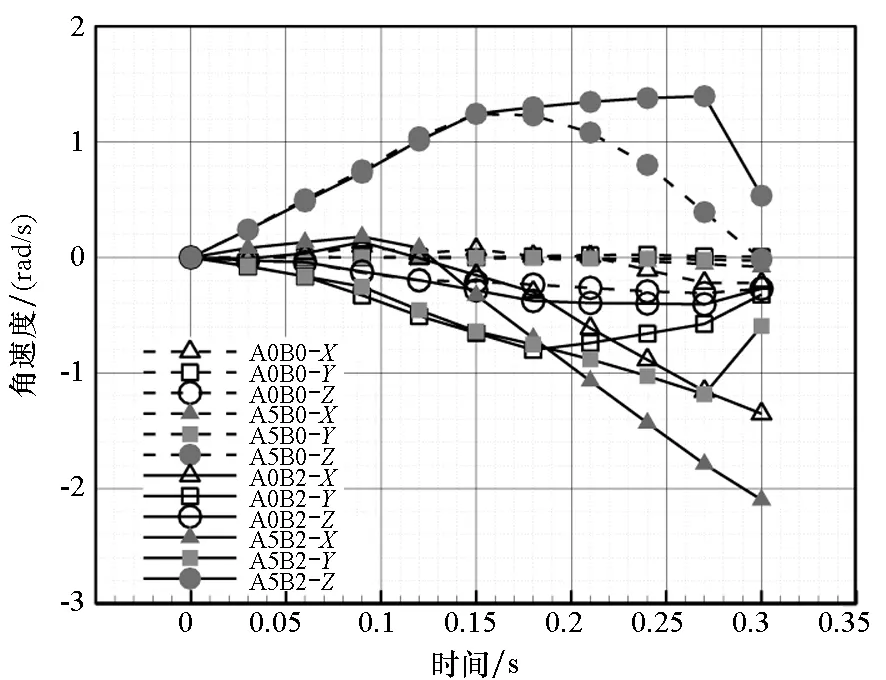
图8 助推器角速度分布Fig.8 Angular velocity distribution for booster

计算得到300 ms内试飞器在A0B0状态下纵向对称面流场密度云图如图9～14所示，图中Rho表示无量纲密度，是流场当地密度与来流密度的比值，该变量的流场等值线分布在一定程度上可反映激波的形态。在初始时刻，来流在前体飞行器头部产生弓形激波，进气道捕捉大部分流量，激波在内流道中经内壁面多次反射交叉后在喷管处膨胀，然后经级间段泄流的气体在后体助推器头部圆顶位置再次产生明显的弓形激波。在60 ms时刻，试飞器整体的激波形态接近初始时刻，从级间段附近网格变化可知后体助推器位置略后移。在90 ms时刻，分离距离继续增大。分离过程对前体飞行器流场形态产生微弱影响，前体尾喷管出口低压区面积增大。在此基础上，分离距离在150 ms和210 ms时刻进一步增大，且助推器姿态及位置发生较明显的变化。至300 ms时刻已基本飞离前体尾流影响域。

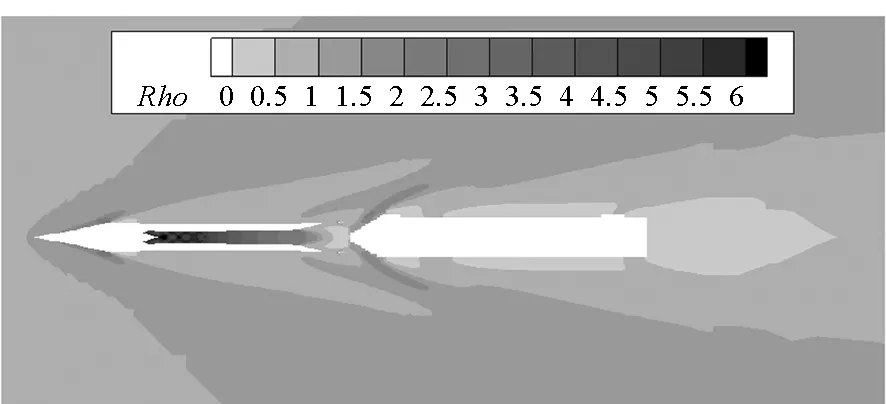
图9 0 ms时A0B0状态流场密度云图Fig.9 Flow field density contour for A0B0 on 0 ms

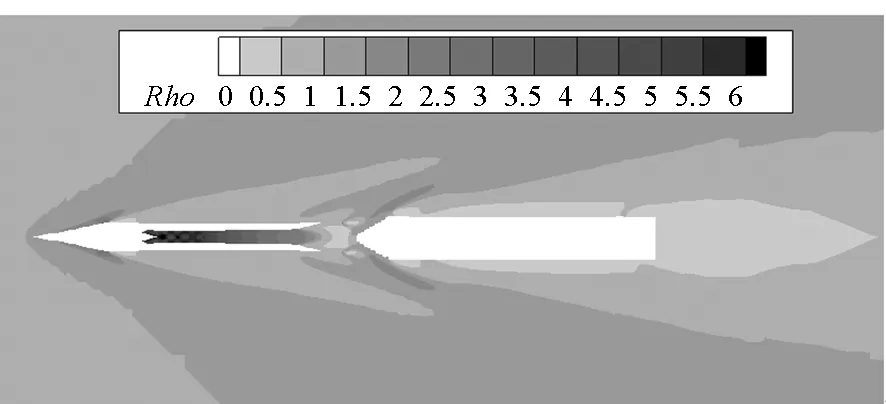
图10 60 ms时A0B0状态流场密度云图Fig.10 Flow field density contour for A0B0 on 60 ms

3.2 气动分析

图11 90 ms时A0B0状态流场密度云图Fig.11 Flow field density contour for A0B0 on 90 ms

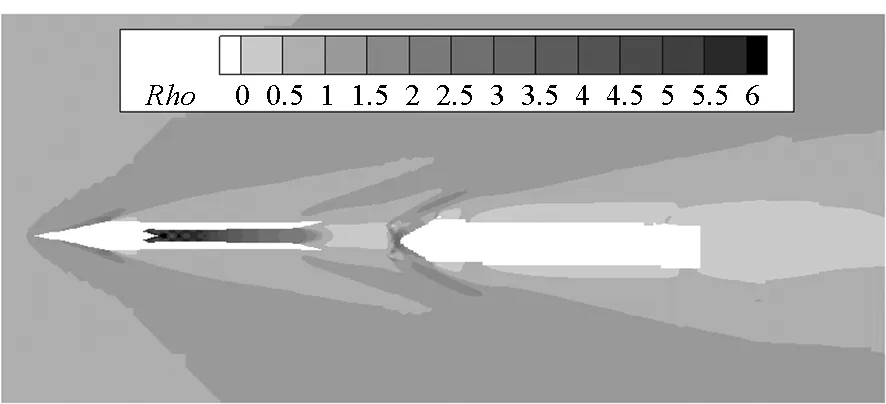
图12 150 ms时A0B0状态流场密度云图Fig.12 Flow field density contour for A0B0 on 150 ms

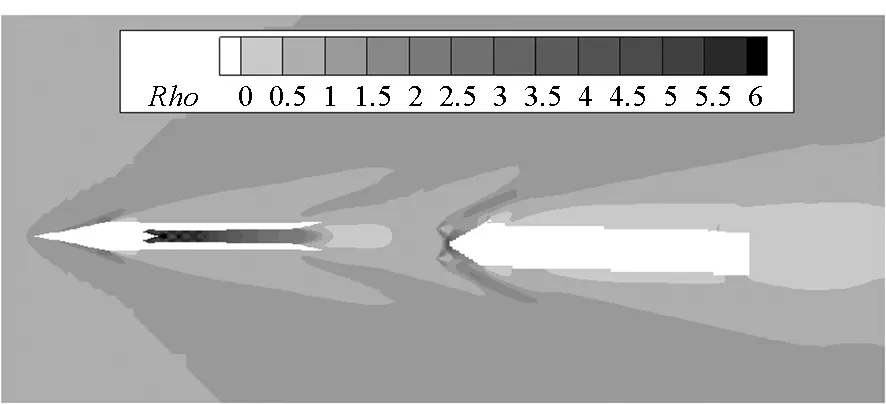
图13 210 ms时A0B0状态流场密度云图Fig.13 Flow field density contour for A0B0 on 210 ms

图14 300 ms时A0B0状态流场密度云图Fig.14 Flow field density contour for A0B0 on 300 ms

图15～18分别给出了飞行器在300 ms分离过程中的升力系数、阻力系数、侧向力系数以及俯仰力矩系数随时间的变化曲线。从结果分析得到，工况A5B2和A5B0气动结果接近，但侧向力系数有差异，这主要是侧滑角方向相对更强的来流条件所致。同时，工况A0B2和A0B0状态下的飞行器气动结果接近，且相对受分离扰动影响更小、数据波动更小。分离初始时期阻力系数变化是分离过程中喷管处压力场差异造成的。从俯仰力矩数据来看：工况A5B0和A5B2状态下飞行器存在低头力矩且有逐渐增大的趋势；而工况A0B0和A0B2存在一个小的抬头力矩且波动较小，这对于飞行器维持静稳定飞行状态更有利。

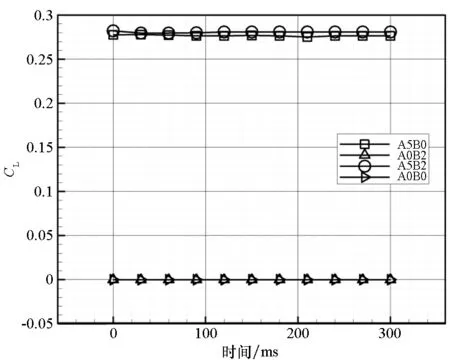
图15 升力系数随分离时间变化曲线Fig.15 Lift coefficient curve on the separation time

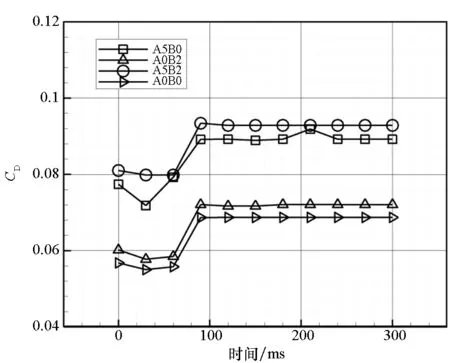
图16 阻力系数随分离时间变化曲线Fig.16 Drag coefficient curve on the separation time

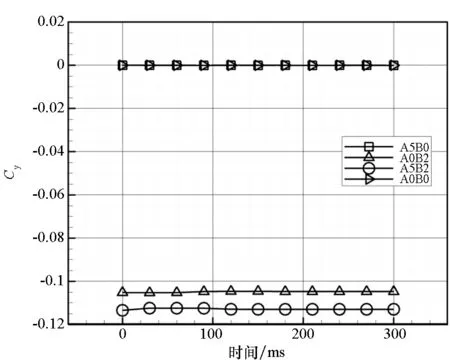
图17 侧向力系数随时间变化曲线Fig.17 Lateral coefficient curve on the separation time

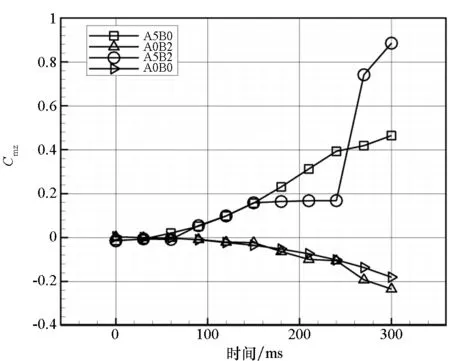
图18 俯仰力矩系数随时间变化曲线Fig.18 Pitch coefficient curve on the separation time

当分离距离大于3倍前体直径，即大于1.2 m时即可认为助推器安全分离。图19为四组算例的飞行器与助推器的分离矢量距离随时间的变化曲线。由图可知，0.3 s内四组工况的分离距离随时间的变化曲线十分接近，均呈抛物线型分布，这说明该方案在弱干扰冷态分离条件下的适应性较好，同时0.3 s计算状态下四组工况均实现了助推器的有效分离。另得到0.1 s时分离距离约为0.3 m，0.15 s时的分离距离在0.6～0.7 m范围内，0.3 s时的分离距离约为2.8 m。同时，由插值方法得到的分离距离对应所需要的时间及对应时刻的分离力如表3 所示。

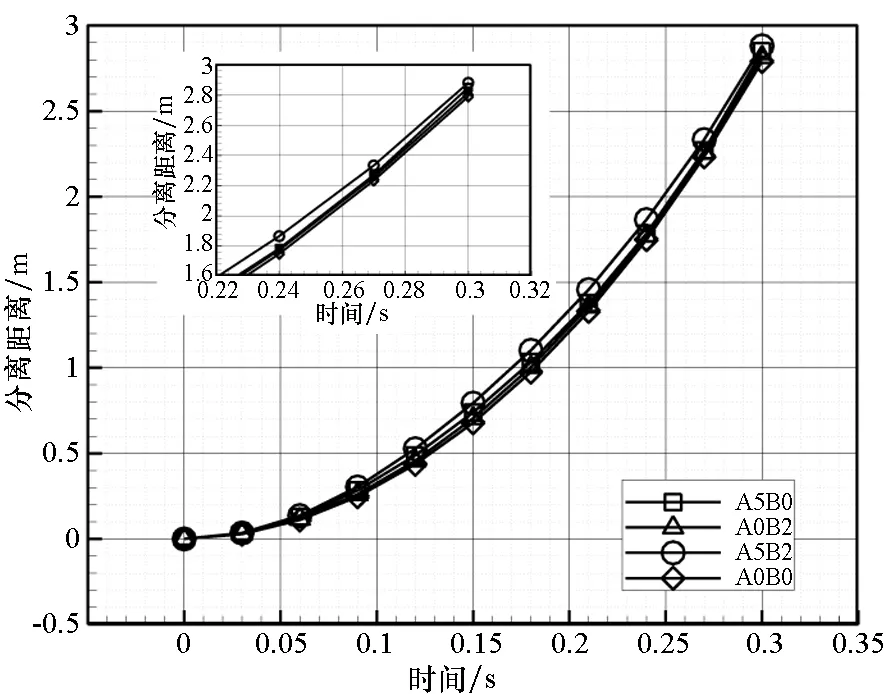
图19 300 ms分离距离随时间变化曲线Fig.19 Separating curves on the 300 ms separation time

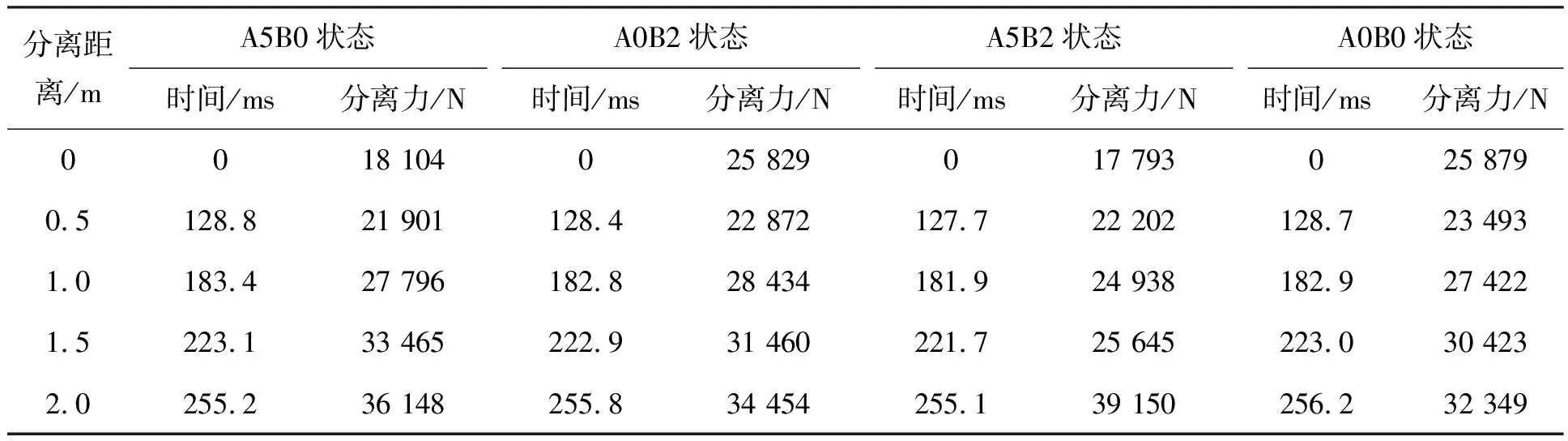
分离距离/mA5B0状态A0B2状态A5B2状态A0B0状态时间/ms分离力/N时间/ms分离力/N时间/ms分离力/N时间/ms分离力/N0018 104025 829017 793025 8790.5128.821 901128.422 872127.722 202128.723 4931.0183.427 796182.828 434181.924 938182.927 4221.5223.133 465222.931 460221.725 645223.030 4232.0255.236 148255.834 454255.139 150256.232 349

4 结论

本文采用动网格技术和非定常数值计算方法评估了带减速板和泄流圆顶分离结构的助推分离方案的可靠性，解决了助推安全分离问题，并得到各时间节点下的分离结构的流场分布。通过对流场结构的分析得到：在分离初期，助推器级间段的圆顶形成了流体滞止区，使前体飞行器尾喷管流场压强增大，导致飞行器气动阻力减小，进而有利于助推分离；随着分离距离的增加，泄流结构对前体阻力干扰减弱，飞行器阻力增大对安全分离产生不利因素，而减速板加快实现了助推器的分离，能够增加中后期的安全分离的可靠性。

通过对气动力结果的分析发现，在初始分离中，前体飞行器的气动阻力存在先减小再逐渐增大的变化趋势，随后保持在一个较初始值更高的稳定值，即在整个分离过程中存在一个分离力极小值，这个结论与流场显示结果吻合。通过对气动参数的变化规律以及分离数据的分析发现，来流干扰因素越少对分离越有利，即攻角和侧滑角均为0时为最佳分离条件。