位阻效应对受阻酚杂化体系阻尼机理的影响
胡乔曼, 徐康茗
(1. 重庆文理学院 新材料技术研究院,重庆,402160; 2.重庆文理学院 材料与化工学院,重庆,402160)
1 引 言
随着城市化进程的不断加快以及高新技术的迅速发展,机械设备等带来的振动问题越发突出并已成为城市发展的制约因素.为了减少振动污染,人们致力于研究振动的控制方法,其中聚合物基阻尼材料因减振性能最为突出而被广泛应用.然而传统的聚合物基阻尼材料(共混、共聚以及IPN结构)以自身黏弹阻尼机理为主,仅通过分子链内摩擦耗散能量,对阻尼性能提升能力有限,已渐渐难以满足设备等对阻尼材料越来越高的要求.因此,如何研究新的阻尼机理、制备新型阻尼材料已成为减振领域急需突破的关键技术问题.
利用动态氢键相互作用增强能量耗散制备阻尼材料,相比于传统阻尼材料,其在动态外力作用下,氢键发生可逆的断裂和重生,吸收大量外部能量,同时引起分子链运动加剧、增大内耗,因此成为极具潜力的阻尼改性机理[1]. 该阻尼机理由吴驰飞等人在研究氯化聚乙烯(CPE)/受阻酚杂化阻尼材料时首次提出[2, 3],且因阻尼改性效果显著,针对该机理的理论研究其后在其他聚合物/受阻酚体系中被广泛讨论.如张立群课题组首次结合分子动力学模拟方法[4],从分子角度探讨了丁腈橡胶(NBR)/受阻酚AO-80杂化体系的阻尼机理,模拟结果表明分子间氢键数目多少,结合能及自由体积大小是阻尼性能高低的决定因素.其后,研究者们在对聚醋酸乙烯酯(PVAc)/AO-70二元体系[5]及NBR/聚氯乙烯(PVC)/AO-80三元体系[6]的模拟研究中,得到了相似的结论.同时郭少云课题组在热塑性聚氨酯弹性体(TPU)/受阻酚AO-70杂化体系的模拟研究中进一步发现,分子间氢键相互作用种类也是影响阻尼性能高低的重要因素[7]. 由此可见,分子动力学模拟方法可有效地对聚合物/受阻酚体系阻尼机理进行分析研究,而且分子动力学模拟方法在其它研究领域也得到了广泛的应用[8, 9],证明此方法是一种非常有效地表征手段. 然而值得注意的是,目前研究者们主要集中于探讨聚合物结构变化对杂化体系阻尼性能的影响,对杂化体系中另一重要组成单元,受阻酚结构变化与阻尼性能间关系的系统理论研究却鲜有关注.
针对这一问题,本文以已有实验研究报道为参考[10],利用分子动力学模拟方法,构建了不同受阻程度受阻酚分子/PVAc杂化体系,重点从理论角度探讨受阻程度与杂化体系阻尼性能间的相互关系,并期望相应的数据能更好地为制备新型杂化阻尼材料提供理论支持.
2 分子模型及模拟方法
2.1 分子模型
本文使用的计算软件是Accelrys的Materials Studio 7.0.首先应用Visualizer模块构建受阻程度由小到大的TDP、AO300及TBBP三种受阻酚分子模型,相应的分子结构如图1所示. 接着参考我们的前期工作[5],构建了一条重复单元数为50的PVAc大分子链.在对受阻酚及PVAc进行优化得到稳定分子结构后(具体优化步骤见1.2),运用Amorphous Cell模块构建了以两条PVAc大分子链为基体的,受阻酚重量分数依次为0、10、20、40、60、80的具有周期性边界的无规盒子,以备后续模拟分析,不同无规盒子中受阻酚添加量如表1所示.

图1 分子模拟中三种不同受阻酚化学结构式(a)TDP;(b)AO300;(c)TBBPFig.1 Chemical structures of (a) TDP, (b) AO300 and (c) TBBP used in the simulation
Table 1 Adding numbers of hindered phenols in different amorphous cells

重量分数(wt%)01020406080TDP048162432AO300035101520TBBP02481115
2.2 模拟方法
模拟温度为25 °C,模拟力场为COMPASS力场,COMPASS力场被广泛用于优化及预测聚合物结构、构型构象、聚集态性能以及分子间相互作用等研究[11].初始速度采用麦克斯韦-玻耳兹曼分布方法在25 °C下得到,verlet速度时间积分法时间步长为1 fs[12].
图2为分子动力学模拟流程:运用Forcite模块对构建的受阻酚及PVAc分子链依次采用最速下降法、共轭梯度法及牛顿方法进行几何结构优化,在此基础上进行动力学优化,系综采用NVT,动力学结构松弛时间总长为2 ns,以得到结构稳定的受阻酚及PVAc分子链 [图2(a)、(b)].根据配比分别构建好相应无规盒子[图2(c)]. 然后对无规盒子进行能量优化,能量收敛方式依次采用最速下降法和共轭梯度法及牛顿方法,接着为了得到几何尺寸最佳以及能量最低的无规盒子,对无规盒子进行动力学模拟,模拟所用系综为NPT系综,所用压力为1 atm,控温方法为Anderden, 控压方法为Berendsen, 动力学结构松弛时间总长为2 ns,其中每隔 5 ps收集一次数据,并采用最后1 ns数据进行结果分析[图2(d)].最后将经过以上优化过程且能量稳定的无规盒子进行分析.采用软件自带氢键计算语言计算体系中氢键个数 [图2(e)], 采用软件自带分析部件计算体系自由体积以及结合能[图2(f)].自由体积计算采用网格扫描方法.

图2 PVAc/TDP分子动力学模拟模型(红色原子是氧原子,绿色原子是氢原子,灰色原子是碳原子,黄色原子是硫原子,蓝色虚线代表氢键)Fig. 2 Models for MD simulation of PVAc/TDP hybrids (red atom is O, green atom is H, grey atom is C, yellow atom is S and blue dashed line represents H-bonds)
3 结果讨论
3.1 氢键相互作用
配对相关函数g(r)可反映以特定原子为球心,在距离r范围内另一原子出现的概率大小,故而被广泛用于研究聚合物体系是否存在氢键相互作用.两原子间距离处于2.6-3.1 Å,3.1-5 Å及大于5 Å分别表示两原子间可产生氢键,强范德华力及弱范德华力相互作用[13].图3以PVAc/TDP-10 wt%模拟体系为例,给出了该杂化体系中分子间氧原子与氢原子随距离改变的配对相关函数.由图可知,配对相关函数的最大峰位于2-3.1 Å区间,说明氧原子与氢原子有较大概率形成分子间氢键相互作用.需要说明的是,其余杂化体系配对相关函数曲线与图3类似,故本文中不再逐一列出.
基于配对相关函数分析,表2 给出了不同杂化体系、不同类别氢键的平均数目.计算方法为分别对经过相同模拟条件的五个能量平衡的无规盒子进行氢键计算,然后求平均值.从表中可以看出,随着受阻酚添加量的增加,受阻程度最小的TDP体系分子间羟基与羰基的氢键数目(TDP Hbondinter)先增加,在80 wt%含量时出现略微的减少,分子内羟基与羟基的氢键数目(TDP Hbondintra)

图3 PVAc/TDP(TDP重量分数10%)混合体系中氢原子和氧原子分子间配对相关函数Fig. 3 Pair correlation function for intermolecular H and O in PVAc/TDP-10 wt% hybrid.

重量分数(wt %)1020406080TDP Hbondinter24798TDP Hbondintra12224AO300 Hbondinter12335AO300 Hbondintra00011TBBP Hbondinter01223TBBP Hbondintra00000
则逐渐增加;受阻程度居中的AO300体系分子间氢键数目逐渐增加,分子内氢键则在较高含量(60、80 wt%)时才观测到;受阻程度最大的TBBP体系分子间氢键数目在10 wt%体系中未能观测到,但随后数目逐渐增加,同时分子内氢键也未能在研究体系中观测到.对上述结果进行比较可知,受阻程度增加,一方面可有效减少受阻酚自身分子内氢键相互作用的形成,也即减少小分子自身团聚倾向;另一方面也增大了受阻酚与聚合物间氢键相互作用形成的难度.
3.2 结合能
结合能(Ebinding)可反映两相互作用组分混合程度,其值可通过分子间相互作用能(Einter)求得[14].而Einter可通过平衡状态下混合体系总能量(Etotal)与单独组分能量差值求得.以TDP体系为例,Ebinding值可通过公式(1)求得:
Ebinding=-Einter=-(Etotal-ETDP-EPVAc)
(1)
其中,Etotal表示杂化体系总能量;ETDP表示TDP总能量;EPVAc表示PVAc 总能量,由于无规盒子中PVAc分子链重复单元数及分子链数目是固定的,因此对于所有杂化体系,EPVAc均为一常值,大小为-1929.97 kcal/mol.
表3 不同杂化体系中不同受阻酚含量的结合能
Table 3 Binding energies of different hybrids with different molecular weights

重量分数(wt%)1020406080Ebinding-TDP(Kcal/mol)386.72-129.01-237.96-501.87-754.02Ebinding-AO300(Kcal/mol)178.88222.77380.62148.36-140.13Ebinding-TBBP(Kcal/mol)161.86154.85148.93142.48121.27
图3为根据公式(1)计算得到的不同受阻酚含量的不同杂化体系的结合能数据.对于TDP体系,受阻酚含量为10 wt%时,其结合能为正值,说明受阻酚与聚合物混合程度较好;继续增加受阻酚含量,相应体系的结合能则为负值,且含量越大,结合能越低,说明受阻酚与聚合物混合程度越来越差,这主要是由于TDP分子团聚所致.对于AO300体系,随着受阻酚含量增加,结合能呈现先增加后降低的趋势,在含量为60 wt%时,也即AO300开始出现分子内氢键相互作用时,结合能开始下降,而含量为80 wt%时,结合能变为负值.对于TBBP体系,随受阻酚含量增加,结合能逐渐降低,但均为正值,说明极性的TBBP能较好地分散在聚合物基体中,但由于位阻作用,两者间结合相对较弱.
3.3 相对自由体积
根据以自由体积理论推导的Williams-Landel-Ferry (WLF)方程可知[15],聚 合物体系中相对自由体积(FFV)受氢键相互作用影响很大.FFV的一般定义如公式(2)所示:
(2)
其中,V和V*分别表示总体积和占有体积.
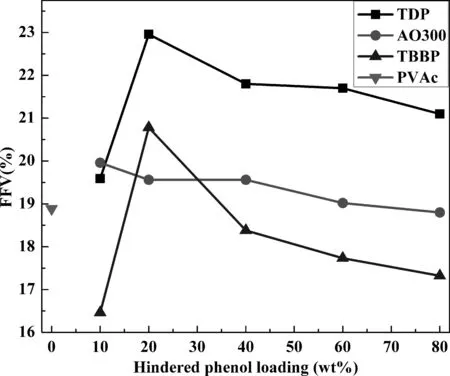
图4 不同杂化体系中相对自由体积随受阻酚含量变化曲线Fig. 4 Fractional free volumes of different hybrids.
FFV常用于描述聚合物体系链堆积程度大小和自由空间数目的多少. 图4为不同杂化体系相对自由体积随受阻酚含量变化曲线. 对于TDP体系,FFV随受阻酚含量增加呈现先增加后降低的趋势,且各含量FFV均大于纯PVAc体系FFV,这同样是由于小分子团聚所致. 对于AO300体系,FFV随受阻酚含量增加而降低,且除了80 wt%体系,其余各含量FFV亦均略大于纯PVAc体系. 对于TBBP体系,FFV同样呈现先增加后降低的趋势,且除了除了20 wt%体系,其余各含量FFV均小于纯PVAc体系,这可能是由于TBBP可较均匀分散于PVAc基体中所致.
3.4 受阻酚扩散系数
图5为不同杂化体系扩散系数随受阻酚含量变化曲线.由于各体系相对自由体积均较小,同时受阻酚分子相对较大,图5中受阻酚扩散系数均较小,说明整个模拟阶段,受阻酚仅在小范围内运动.但值得注意的是,相较于受阻程度最小的TDP及受阻程度最大的TBBP,除极个别情况外,受阻程度居中的AO300扩散系数均更大些,说明小分子团聚及较大的位阻作用均不利于受阻酚小分子扩散,而AO300更大的扩散系数更有利于其与聚合物间形成结合能力更强的分子间氢键相互作用.
综上,受阻程度最小的TDP体系,可形成较多的分子内及分子间氢键相互作用,但由于较易形成小分子团聚,其与聚合物混合程度较差、同时自身运动受限导致相对自由体积加大,这些因素均不利于阻尼性能的提高.受阻程度最大的TBBP体系,形成分子间氢键相互作用较少且与聚合物间结合较弱,导致其更多地是以普通极性分子的形式分散于聚合物基体中,分子间氢键作用效果不明显,同样不利于阻尼性能的提高.受阻程度居中的AO300体系,在一定含量下可形成适中的分子间氢键相互作用与结合,有利于发挥氢键作用提升阻尼性能,但过高含量同样可导致其形成小分子团聚降低阻尼性能.
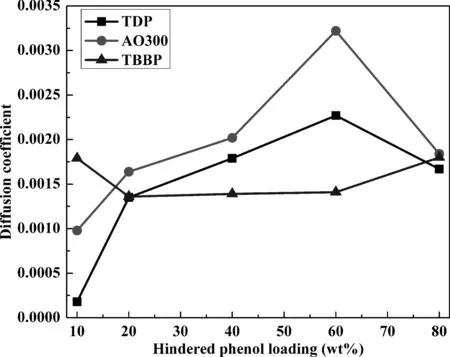
图5 不同杂化体系中扩散系数随受阻酚含量变化曲线Fig. 5 Diffusion coefficients of different hybrids
4 结 论
本文通过对受阻程度不同的三种受阻酚小分子/PVAc体系进行分子模拟分析,揭示了位阻效应对杂化体系阻尼机理的影响,主要结论如下:
(1)受阻程度增加,杂化体系分子内及分子间氢键相互作用减弱,其中分子内氢键相互作用弱化效果更明显,可有效减少小分子团聚倾向.
(2)小分子团聚及过大的位阻效应均对受阻酚运动产生阻碍作用,不利于受阻酚与聚合物形成强烈氢键相互作用,从而使结合能偏低,同时小分子团聚使得相对自由体积较大,过大位阻效应使得氢键作用难以发挥,这些均不利于阻尼性能的提高.
(3)合适的位阻既能减小小分子团聚,同时对受阻酚运动阻碍作用较小,可使得其与聚合物基体形成强烈的氢键相互作用,利于阻尼性能的提升.

