响应变量缺失下部分线性模型的异方差检验

刘 锋，胡 悦，康新梅

(重庆理工大学 理学院， 重庆 400054)

部分线性模型是20世纪80年代发展起来的一类重要的统计模型，既包含了参数部分，又包含了非参数部分。部分线性模型融合了参数模型和非参数模型的优点，可以概括和描述现实中的许多实际问题，较单纯的参数模型或非参数模型具有更大的适应性、更强的解释能力。因此，该模型引起了广泛的重视和研究，在工业、农业、经济、生物统计等领域得到了广泛的应用。

在实际问题中，往往由于诸多原因导致数据缺失，比如获取数据花费的代价大、研究个体由于药物的副作用而停止试验等。用缺失数据拟合模型的统计推断已经有很多的研究，但是大部分的研究还是在模型的估计方面。如果用错误的模型拟合数据，得到的结果可能是不合理的，所以关于模型的检验具有非常重要的意义。

在回归模型中，一般假定模型的误差项εi是相互独立的，且具有相同方差的随机变量。对于一个拟合理想的模型,残差中不再含有模型的信息，即残差为白噪声序列，所以模型的误差项的独立同方差是模型的一个基本假定。如果模型存在异方差会导致参数估计量非有效，变量的显著性等检验失去意义，会出现模型预测失效，甚至模型被误用等问题。因此，在统计推断之前，检验模型是否具有异方差是非常有必要的。

考虑如下部分线性模型：

(1)

其中：β0是p维参数向量；g(·)是未知函数；{(Xi,Ui,Yi),1≤i≤n}是来自(X,U,Y)的独立同分布样本；εi是随机误差，且几乎处处有E(εi|Xi,Ui)=0。 通常假设Ui的维数为1。不妨设Ui∈[0,1]，此时g(·)为定义在[0,1]的未知函数。

1 方法和主要结果

1.1 响应变量缺失的处理方法

假设响应变量Y是随机缺失(MAR)的，即在给定X和U时，Y是否缺失与Y的值条件独立。定义δi为指示第i个个体的响应变量值Yi是否缺失的变量，当Yi观测到时δi=1，当Yi缺失时δi=0，MAR缺失机制表示为P(δ=1|Y,X,U)=P(δ=1|X,U)。 MAR是经常使用的缺失机制之一并且与很多实际情况基本吻合，可以参考文献[1]。 假设得到了模型(1)的一个随机样本(Yi,δi,Xi,Ui),i=1,2,…,n。

首先估计参数β0，将式(1)两端分别乘以δi可得

再将上式两端取关于Ui的条件期望，得

E(δi|Ui=u)g(u)

由此可得

其中:

g1(u)=E(δX|U=u)/E(δ|U=u)

g2(u)=E(δY|U=u)/E(δ|U=u)

那么它们对应的估计量是

和

(2)

当Yi缺失时，用回归借补的思想对Yi进行补齐，

1.2 异方差检验的方法

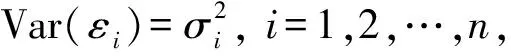
(3)

下面考虑模型(1)响应变量随机缺失下的异方差检验问题。

假定模型的随机误差项εi,i=1,2,…,n,有E(εi)=0,Var(εi)=σ2·mi,其中mi>0,假设mi满足下面的函数形式：

mi=m(zi,γ),i=1,2,…,n

其中mi仅取决于q×1维向量zi和q×1维的未知参数γ。接下来假定m(·)是关于γ的可微函数且存在一个唯一的γ的特定值γ*使得对于所有的zi，使得m(zi,γ*)=1。因此检验模型(1)的异方差性等价于检验下面的假设：

H0:γ=γ*↔H1:γ≠γ*

为构造经验似然比，定义如下估计方程：

其中：

i=1,2,…,n

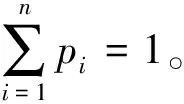
上述经验似然比函数不仅含有未知讨厌参数β0，σ2和感兴趣的参数γ,而且还包含未知函数g1(·),g2(·)， 因此L(γ,β0,σ2)不能直接用于统计推断。一个直接的想法是分别利用它们各自的估计来代替，利用上述所介绍的估计方法得到它们的估计量。

代入未知函数及参数β0的估计量，得到估计函数：

其中

i=1,2,…,n

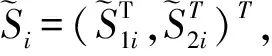
利用Lagrange乘数法求得pi的最优值为

其中λ为下面方程的解：

所以可以得到

(4)

接下来将通过一些假设条件，建立经验似然的非参数版本的Wilk’s定理，具体假设如下：

A3:wnj(t)满足一阶Lipschitz条件;

A4:g(·),g1(·),g2(·)满足一阶Lipschitz条件;

A6:Cov(xi-E(xi|ti))为正定阵;

A7:

且矩阵A11和A22正定。

定理1 在零假设及假设条件A1～A7下，当n→∞时，l0(γ,σ2)具有自由度为q+1的渐近卡方分布，即

为了处理讨厌参数σ2，定义

l0(γ)

则在上述假设条件及零假设下，当n→∞时，有[7]

2 数值模拟

本节通过数值模拟来研究本文提出的基于经验似然的异方差检验方法的可行性。

为了简单起见，考虑如下模型：

核函数K(·)为Beweight核:

考虑下面4种响应变量缺失情形：

情形A:

P(δ=1|X=x)={1/(1+0*exp(x))}

情形B:

P(δ=1|X=x)={1/(1+0.1*exp(x))}

情形C:

P(δ=1|X=x)={1/(1+0.25*exp(x))}

情形D:

P(δ=1|X=x)={1/(1+0.65*exp(x))}

这4种情形下，平均缺失率分别约为:0、0.1、0.2、0.4。样本量n=100,200,300,各进行1 000次模拟，显著性水平α=0.05。结果如表1所示。

从表1、2的模拟结果来看，不论误差服从正态分布还是均匀分布，都可以得到比较满意的结果。当在同一缺失情形下，随着样本量的增大，检验的准确度随着提高：在原假设(γ=0)下，检验水平(size)逐渐接近显著性水平0.05；在备择假设下，功效(power)逐渐接近于1。但可以看到，在原假设下，当小样本时，检验水平(size)偏高，这主要是由于经验似然比检验统计量是渐近服从卡方分布的。当样本量一定时，随着缺失率的增大，检验的准确性随着降低，如表2所示，在缺失情形A、B、C、D下，当n=300时，在原假设(γ=0)下，检验水平分别为0.050 3、0.050 4、0.050 8、0.051 0，随着缺失率的增大检验水平增大，但还是能达到比较满意的效果。以上模拟结果可以说明：缺失率越大，即数据的完整性越低，检验的不稳定性和不准确性越大。但是在缺失率增大时，得到的结果依然比较满意，这说明运用本文提出的方法对响应变量缺失下部分线性模型进行异方差检验的效果是比较好的。

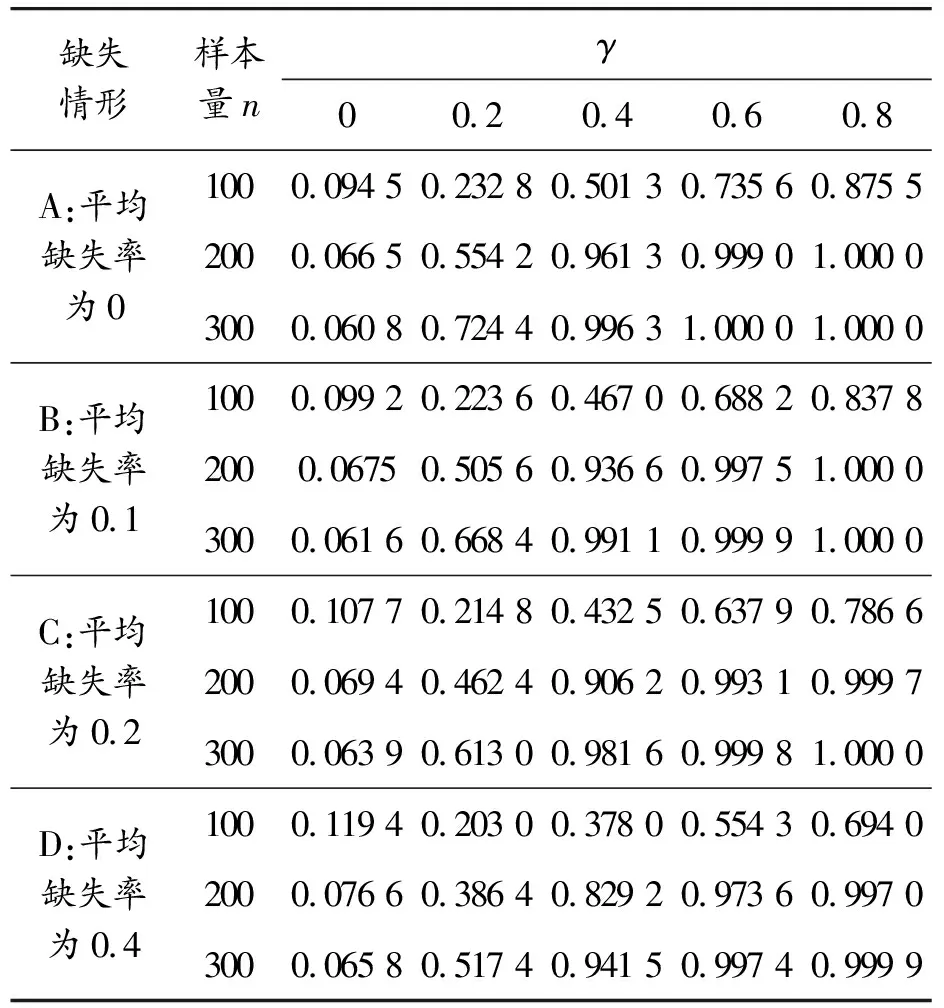
表1 不同缺失情形下经验似然比检验结果(误差服从正态分布)

表2 不同缺失情形下经验似然比检验结果(误差服从均匀分布)

3 定理的证明

为了给出主要结果的证明，首先给出如下引理。

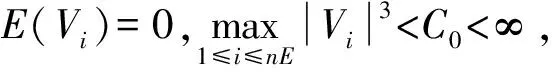
1) 存在绝对常数C1>0,C2>0,使得关于t∈[0,1]一致地有：

对充分大的n成立。

2) 存在绝对常数C3>0使得关于s,t∈[0,1]及n≥1一致地有：

那么对充分大的n有

证明过程见文献[8]。

注权ani(t)为随机时结论依然成立，见文献[10]。

引理2 在假设条件A1～A6以及零假设下，有

证明由假设A1～A6与引理1即得,见文献[8]。

引理3 设

b1≥b2≥…≥bn≥0,

M=max{S1,…,Sn}

则

(5)

为了应用Abel不等式，式(5)可变形为

(6)

其中(j1,j2,…,jn)为(1,2，…,n)的任意重排。若序列bi的非负性限制去掉，有

(7)

对式(7)的后两项分别进行如式(6)的处理，最后得到：对任意2个序列{ai},{bi},总有

(8)

其中(j1,j2,…,jn)为(1,2，…,n)的任意重排。

(9)

证明过程见文献[9]。

(a)A>0⟺A22>0,A11.2>0

(b) 若A22>0,则A≥0⟺A11.2≥0

证明过程见文献[11]引理3.2.1。

引理6 在零假设及假设条件A1～A7下，有

证明首先证明

接下来证明：

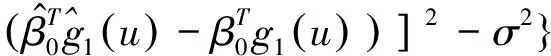
又有

由引理2，有

由引理2,式(8)及(9)可得：

其中(j1,j2,…,jn)为(1,2,…,n)的任一置换。因此，Δn2=op(1),Δn3=op(1)。

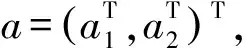
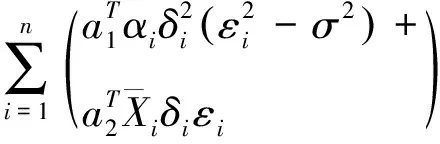
记ε的i阶矩为μi,P(δ=1|X,U)=p,有Ε(ζi)=0及

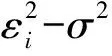
为正定矩阵。

因此，

当n→∞时,从而可得

由上述结论及条件A5,可得Lindeberg条件成立。由Lindeberg中心极限定理，有

从而由Cramer-Wold方法，有

引理7 在零假设及假设条件A1～A7下，有

证明定义

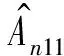
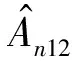
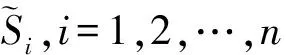
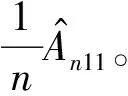
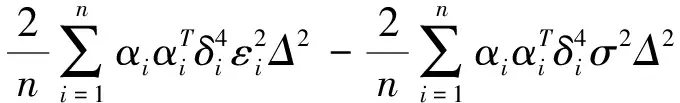
Rn4+Rn5+Rn6-Rn7

由假设条件A7与引理2，有

接下来考虑Rn3中的一项

由假设A5、 A7、 引理2以及大数定理，对任意q+1维非零向量θ，有

因此，

Rn1=op(1),Rn3=op(1),Rn4=op(1)

Rn5=op(1),Rn6=op(1)

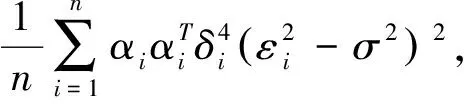
由大数定理得

从而

同理

再由文献[4]引理2，有

引理 7得证。

证明类似于文献[2]。

引理9 在假设条件A1～A7及零假设下，有

证明类似于文献[3]的引理3。

定理1的证明：

由引理8及引理9，将式(4)泰勒展开，可以得到

由引理6～9,文献[7]中定理3.5,通过简单的计算，有

l0(γ,σ2)

最后结合引理6、引理7，定理得证。具体证明类似于文献[12]。