让数学生活化之教学反思

湖北省宜昌市夷陵区龙泉镇土门初级中学 文 图 汪艳红

一、学生对数学学习的态度调查

作为数学教师，我真实感受到学生对数学的厌恶。曾经我调查过那些数学成绩优异，考上重点大学的学生，他们的回答让我百思不得其解。

问题调查情况如下：

问：你眼中的数学是什么样子的?

答：是一些居心叵测的成年人为学生挖的陷阱；数学问题是一些仅仅出现在数学课本和试卷上的，让某些老师看着学生崴脚而感到窃喜的东西！

问：数学老师是什么样子？

答：一个高明的数学老师只是一个针对学生挖坑布雷，用心险恶的高手，那些难题只是数学老师克敌制胜的“独门秘籍”。

为什么数学课让学生如此厌恶？为什么数学老师在学生眼中如此“险恶”？通过和他们的交流我明白了，他们眼中的数学课除了计算便是作图和证明，那些东西枯燥、乏味，只会出现在试卷上，从不会出现在生活中，学习多年数学的学生从未感到数学与实际生活的联系，从未感受到数学的价值，难怪他们有如此想法。

二、数学教学反思

我开始反思自己，我的数学教学进入了一个误区：自己不停地讲数学，不停地带着学生做练习题，学生在不断练习中越来越不喜欢上数学了！我忽视了数学知识的来源，把数学简单归结为计算、作图和证明！数学离开了生活的源泉，缺少生活中的应用就变成了一个个知识点，没有了源与流，没有了生命力，活生生的数学变成了变成死板的机械训练。于是我开始尝试让学生学习生活中的数学，学习有用的数学。经过多年实践，我逐步有了自己对数学课的一点想法，下面以坡角、坡度为例说说我的实践。

创设一种现实数学情景引出课题。小时候，我们玩打沙包，不小心沙包扔到屋顶上去，你怎么取下来？（学生回答用棍子挑，搭梯子上去）顺便讲个小故事：我小时候搭梯子上屋顶，不小心摔下来，至今腿上还有一道疤。老人们常说“三天不打，上房揭瓦”（学生开始笑了），放梯子时一定要放平些，陡了容易摔下来。那么平与陡是如何判断的？今天我们就从梯子的倾斜度谈起。

出示一组关于梯子实物图，让学生判断哪个梯子平些，哪个梯子陡些，并说明理由。根据学生说理介绍坡角、坡度的定义，让学生通过自己作图，将概念转化直角三角形形中去。之后出示三道简单填空题，让学生巩固定义。在学生熟知定义及其与解直角三角形的关系的前提下联系生活，用数学知识解决生活中的问题。

问题1：一个公共房屋门前的台阶共高出地面1.2米（如图1所示），台阶被拆除后，换成供轮椅行走的斜坡。根据这个城市的规定，轮椅行走斜坡的倾斜角不得超过30°。从斜坡的起点至楼门的最短水平距离该是多少？（精确到0.1米）

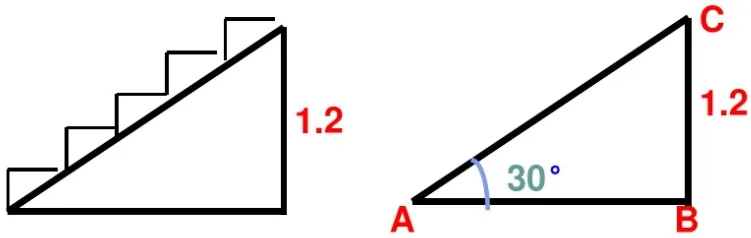
图1

出示实物图，要求学生根据实物图转化几何图形并求解。这个问题较简单，学生很快得到答案。

问题2：20米高的7层楼着火，消防车赶来救火。云梯最大倾斜度为60°，展开最大距离为25米，车身高度2米，楼体15米以内消防车无法到达。请根据以上信息设计营救方案，并说明此次行动能否成功营救7楼被困人员？（如图2所示）

图2

这个问题开放程度比较大，很多学生感觉无从下手，于是引导他们：解直角三角形必须知道几个元素？本题中可以确定几个元素？需要再确定哪个元素就可以求解？在我的引导之下，一部分孩子开始尝试确定最大角；确定云梯最大边。终于有人提出了合理的方案，虽然解决方案不是我想要的那么全面，但是这只是一个开端，我相信这样的问题一定会开发学生的思维，激起他们学习数学的兴趣。等到有了结论，我也少不了啰嗦几句：“水火无情，性命攸关，千万不能粗心大意！”

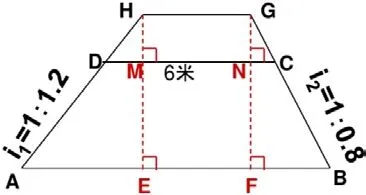
问题3：为了增加抗洪能力，现将横断面如图所示的大坝加高，加高部分的横断面为梯形DCGH，GH∥CD，点G、H分别在AD、BC的延长线上，当新大坝坝顶宽为4.8米时，加固这样的大坝1000米，需要付给农民工多少工资？（每立方米300元）

这个问题与实际生活联系比较紧密，学生虽然都在积极思考，但一时又找不到突破口。好在经过小组讨论，一部分学生开始解决问题。一个女孩代表本组进行讲解：要求付给农民工多少工资，需要求出新增大坝的体积，即先求出新增大坝高，再求横截面。如何求高？GH∥CD，∠HDM=∠A，即HM∶DM=1∶1.2，同理得GN∶NC=1∶0.8，设HM=x，表示出DM，NC，从而求出新增坝面的高，再求体积……她的发言得到了大家的热烈鼓掌，下面有人说我也是这样做的。可惜下课时间到了，这个问题解决有些匆忙。

反思本节课，我觉得它体现了我一直坚持的“学生活中的数学，学有用的数学”。让同学们觉得数学知识有用，能解决实际生活中的问题，这样他们就会慢慢喜欢数学，慢慢体会数学的价值。但这节课也有太多遗憾，比如说问题2,3难度较大，大部分学生无法独立完成，课堂气氛有些沉闷，学生参与程度不是很高。但我坚信生活中的数学一定会为数学课堂增加魅力，一定会让数学课堂接上地气。