梯度纳米结构IF钢的协同强化本构模型
,,,
(浙江工业大学 机械工程学院,浙江 杭州 310014)
纳米材料具有优异的性能[1-2],但是韧性和塑性却往往较低,为了克服纳米材料的这一缺点,卢柯等在1999 年提出了梯度纳米结构材料的概念,该材料在空间上呈现出由纳米级到微米级的梯度变化[3]。梯度纳米结构有别于不同特征尺寸结构的简单混合,没有明显的界面,因此可以有效避免尺寸突变引起的性能突变[4]。梯度纳米结构金属具有明显的强化效果,梯度层的屈服强度远高于基体。研究表明:梯度纳米结构金属在强塑性匹配[5]、抗疲劳[6]和抗磨损[7]等方面具有非常突出的性能。
近年来,有限元模拟成为研究材料力学性能的一个重要手段。早期关于梯度纳米结构的研究中,Wei等[8]将梯度材料简化为同轴壳体和芯部,并调整壳体失效应变和整体的体积分数,研究了这两个参数对材料整体拉伸性能的影响。Petit等[9]将梯度层分为纳米层和过渡层,采用混合法则(The rule of mixture,ROM)和反演分析,获得了纳米层的应力—应变关系,并成功预测了拉伸试样的颈缩点。Wu等[10]和Li等[11]提出了更加接近真实情况的多层模型,他们通过机械减薄的方法制备试样,并采用拉伸实验逐层测定材料的应力—应变关系。在Wu等[10]的研究中,考虑到材料梯度变化对各层力学性能的影响,需要尽可能减薄每层材料的厚度,这对试样的制备是一大挑战。此外,多层模型将梯度结构划分为多个孤立层,无法考虑各层之间的相互作用,因而梯度纳米结构中存在的协同强化效应在多层模型中无法体现。为了简单快速获取梯度纳米结构材料的应力—应变关系,同时又体现材料的协同强化作用,需要提出新的方法。笔者首先基于显微硬度—拉伸应变之间的实验数据,利用显微硬度与材料屈服强度之间的定量关系,建立每层材料的Hollomon型应力—应变硬化准则和GTN损伤模型,进而通过参数反演获得材料参数;接着,利用上述本构关系,采用基于混合法则的多层模型,建立有限元模型并进行系统计算;然后,对比分析有限元模拟结果与实验数据,检验本构关系的有效性;最后,详细分析多轴应力状态的演化,并预测失稳状态发生的临界条件。
1 梯度纳米结构材料的本构关系
1.1 弹塑性本构模型
梯度纳米结构薄板如图1所示,芯部是粗晶基体,上下表层为梯度纳米结构层,晶粒尺寸由表及里呈现梯度分布。对应于晶粒尺寸的梯度变化,梯度纳米结构材料的屈服强度由表及里呈梯度降低。单向均匀拉伸的开始阶段(轴向应变ε在横截面yz上均匀分布),芯部材料首先发生塑性屈服并进入应变强化,而表层梯度纳米结构层仍处于弹性阶段。随着ε的进一步增加,屈服区域由芯部逐渐向表层扩展,直至全截面屈服。材料发生塑性流动所需的轴向拉力,随着变形量增大而增大。塑性流动所需的真实应力,等于该时刻的材料屈服应力,亦称流动应力。

图1 梯度纳米结构薄板Fig.1 Schematic of gradient nanostructured plate
梯度纳米结构试样单向拉伸(或压缩)时,若材料处于弹性变形阶段,轴向应力σ与轴向应变ε满足胡克定律,即
σ=Eε
(1)
弹性模量E作为一个表征原子间结合力大小的力学指标,晶粒尺寸对其影响可以忽略不计,于是假设梯度纳米结构材料与粗晶材料具有相同的弹性模量。由单调拉伸实验[10]可得:弹性模量E=210 GPa和泊松比ν=0.3。随着拉伸载荷的进一步增大,材料进入塑性屈服阶段,此时假设所有材料单元都遵循Hollomon硬化准则,即
Θ=KεN
(2)
式中:Θ为屈服应力;K,N分别为应变硬化系数和应变硬化指数。梯度纳米结构材料力学性能的梯度变化,使得屈服应力Θ与相对于表层的位置有关,即该参数为坐标z的函数,因此无法基于常规拉伸实验结果确定其数值。
梯度纳米结构薄板发生轴向拉伸时,由于应变硬化效应,不同深度下的显微硬度都将随着轴向塑性应变的增大而增大。Wu等[12]测量了梯度纳米结构IF钢在4 个不同轴向拉伸应变(ε=0,0.048,0.095,0.223)下的维氏显微硬度,获得了不同应变下显微硬度沿梯度纳米结构厚度方向的分布,结果如图2所示。由文献[13-14]可知:材料的屈服应力或流动应力可由显微硬度换算而来,两者存在的线性关系为
Θ=λ·Hv-σ0
(3)
式中:Hv为维氏显微硬度;λ,σ0分别为材料常数。由于式(3)对于同一种材料具有通用性,因此可认为式(3)适用于梯度纳米结构材料的任一材料单元。通过式(3)把实验测量的显微硬度转换为流动应力,可得不同轴向拉伸应变下流动应力(屈服应力)Θ沿梯度纳米结构层厚度方向的分布,即Θ(z)。当轴向拉伸应变为0时,材料没有发生应变硬化,此时测量所得的显微硬度对应于初始屈服应力Θ0(z)。

图2 不同拉伸应变下的显微硬度分布Fig.2 Microhardness distribution under different tension strains
此外,韧性金属材料拉伸过程中,伴随着微孔洞的形核、长大和聚合,材料内部的损伤不断累积,直至试样发生宏观断裂。GTN模型可以较好地表征上述材料损伤机制,其屈服面方程[15-16]为
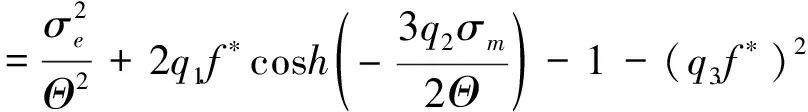
(4)
式中:σe为Mises等效应力;σm为静水压力;q1,q2,q3为损伤参数;f*为孔洞体积分数函数。当不考虑损伤时,即f*=0,GTN模型退化为Von Mises屈服准则。令f,fc,ff分别为孔洞体积分数、开始聚合时的临界孔洞体积分数以及材料断裂时的临界孔洞体积分数。若f≤fc,则f*=f;若f>fc,则f*=fc+(1/q1-fc)(f-fc)/(ff-fc);若f≥ff,则f*=1/q1。孔洞体积分数f的损伤演化方程[15-16]为
(5)
1.2 应变硬化参数的识别
为了得到流动应力与显微硬度的转换关系,需要确定式(3)中的常数λ与σ0。Keryvin等[17]指出:铁基金属材料的λ值可取为2.8。由实验[12]可知:粗晶IF钢的初始屈服应力和维氏显微硬度值分别为46 MPa和Hv=21.8 kg/mm2(0.213 GPa)[10],则由式(3)可得σ0=15.1 MPa基于梯度纳米结构IF钢在4 个不同轴向拉伸应变(ε=0,0.048,0.095,0.223)下的维氏显微硬度,利用显微硬度与流动应力的关系式(3),可以得到4 组流动应力—深度的数据,结果如图3所示。由于梯度结构的微观组织结构由表及里呈现梯度变化,当进入塑性屈服阶段后,即使轴向变形相同,轴向应力—轴向应变响应也会呈现梯度变化。因此,把梯度纳米结构层划分成等厚度的12 个薄层,每层的厚度为10 μm,假设每层材料具有相同的力学性能。利用Hollomon硬化准则式(2)拟合每一薄层材料的流动应力—轴向应变,结果如图4所示,拟合得到的应变硬化系数K和应变硬化指数N列于表1。

图3 不同轴向拉伸应变下的流动应力分布Fig.3 Flow stress distribution under different tension strains

图4 各层材料的应力应变关系Fig.4 The stress-strain relationships of each layer
Table1MaterialparametersofHollomonhardeningruleofeachlayer
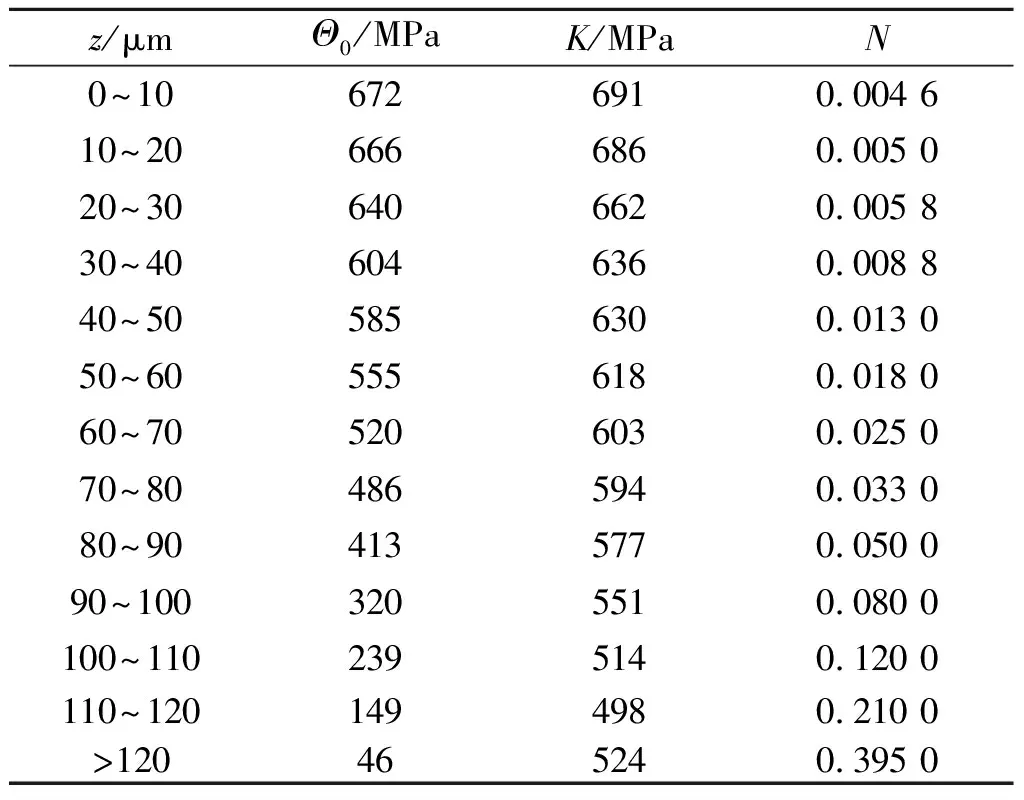
z/μmΘ0/MPaK/MPaN0~106726910.004 610~206666860.005 020~306406620.005 830~406046360.008 840~505856300.013 050~605556180.018 060~705206030.025 070~804865940.033 080~904135770.050 090~1003205510.080 0100~1102395140.120 0110~1201494980.210 0>120465240.395 0
轴向均匀拉伸变形的梯度纳米结构材料薄板(图1),横截面上的总轴向拉力F由粗晶层和梯度结构共同承担。当薄板为纯弹性变形时,轴向应力在横截面上均匀分布;若芯部进入塑性变形阶段,而梯度纳米结构层仍为弹性变形时,虽然总轴向应变相同,但轴向应力在横截面上不再均匀分布。为了建立解析表达模型,假设梯度层中每一薄层内的轴向应力σi相等,并令Fi表示第i层的轴力。而粗晶层内晶粒尺寸相同,因此粗晶层内的轴向应力σcg也相等,其合力为Fcg。基于混合法则(ROM),可得
(6)
相应的轴向名义应力表达式为
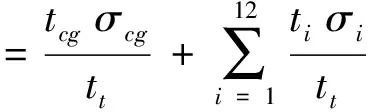
(7)
式中:tcg,ti分别为粗晶层和梯度结构第i层的厚度;tt为薄板总厚度。由文献[10]中的试样尺寸可知:tcg=380 μm,ti=10 μm,tt=500 μm,此时梯度结构占比为24%。σcg,σi可分别由胡克定律式(1)和Hollomon硬化准则式(2)得到,进而由式(7)计算出不同轴向应变时梯度纳米结构材料的名义轴向应力Π,结果如图5所示。显然,数值预测结果与实验数据[12]吻合较好,验证了表1中应变硬化参数的有效性。
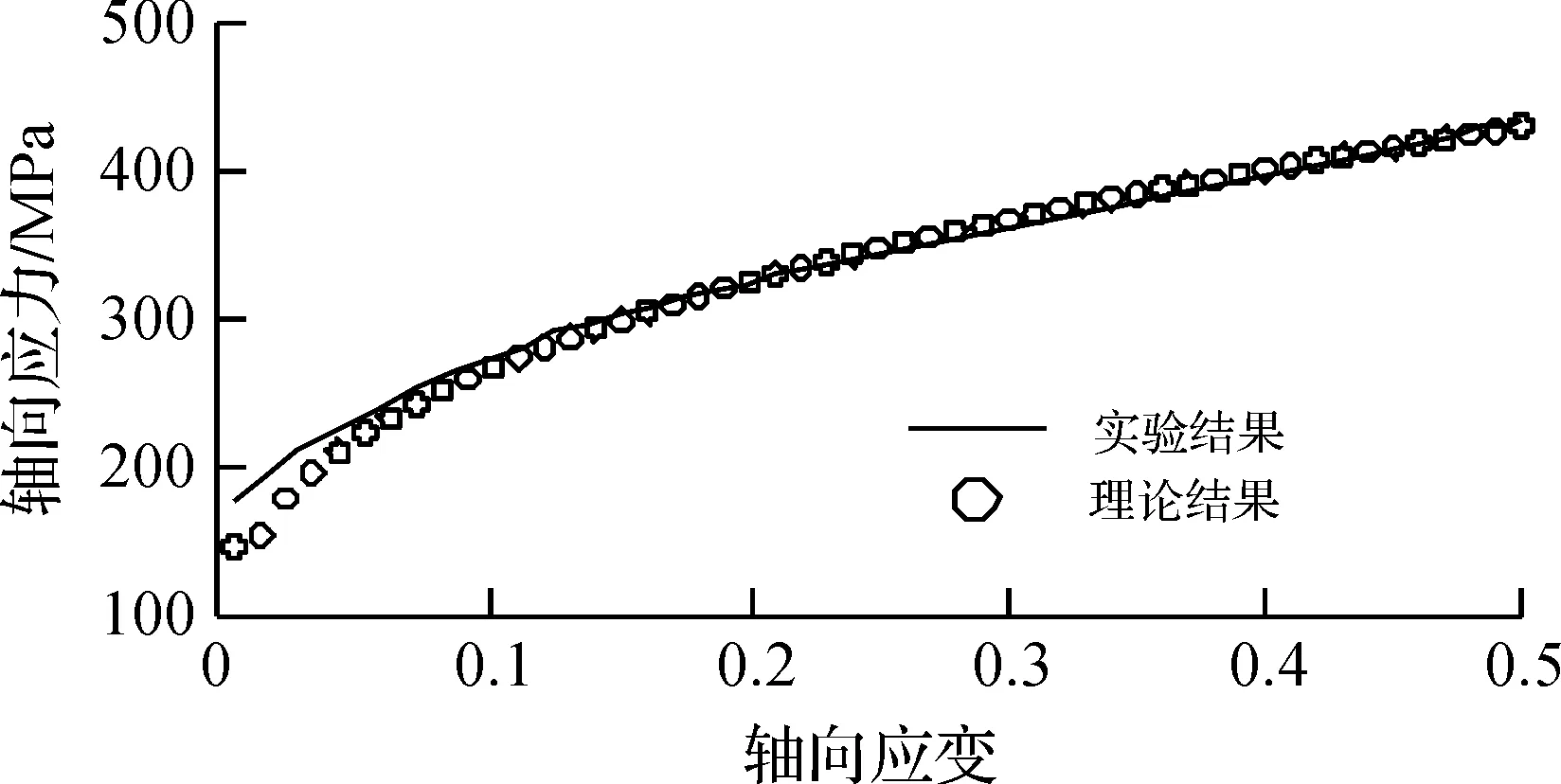
图5 梯度纳米结构 IF钢的轴向应力—轴向应变曲线Fig.5 Axial stress-axial strain curve of gradient nanostructured IF steel
1.3 损伤参数的识别
在1.1中定义了9 个用于描述材料孔洞演化的参数。通常认为q1,q2,q3与材料无关,其值取为q1=1.5,q2=1.0,q3=2.25。初始孔隙率f0可由材料组成确定,其值可取为0.002[15]。与空洞聚合相关的损伤参数εN,SN,对于多数材料来说是独立的,一般取为εN=0.3,SN=0.1。因此,需要基于实验结果确定的损伤参数只有fc,fF,fN。
基于拉伸试样的对称性,建立如图6所示的1/8有限元分析模型,用Abaqus进行计算。为了模拟梯度纳米结构层的力学性能和应力应变响应的梯度变化,网格划分时遵循表层密集芯部稀疏的原则,单元类型为C3D8R。在试样端部受到拉伸载荷作用时,中间标距段内具有相同的轴向应变。由于梯度纳米结构层与粗晶层的微观组织不同,因此GTN模型中各自的损伤参数也不相同。为了简便起见,有限元模拟时采用2 套损伤参数(表2),分别应用于梯度结构层与粗晶层,而不再对梯度结构层做进一步细分。通过有限元计算,得到了拉伸试样的6 组载荷—位移曲线,如图7所示。由图7可知:No.2损伤参数的模拟结果与实验结果[12]吻合程度最高。因此,梯度结构层的损伤参数初步定为,fc=0.15,fF=0.25,fN=0.001,粗晶层的损伤参数为fc=0.15,fF=0.25,fN=0.01。

图6 梯度纳米结构薄板的1/8有限元模型Fig.6 Finite element model of gradient nanostructured plate

No.梯度层fcfFfN粗晶层fcfFfN10.150.250.0010.150.250.03320.150.250.0010.150.250.01030.150.250.0010.150.250.00140.150.250.0010.150.500.01050.150.250.0010.250.250.01060.150.250.0100.150.250.010

图7 轴向载荷—位移曲线Fig.7 Relationships between axial load and axial displacement
建立梯度层占比为16%,30%的有限元模型,验证上述损伤参数的有效性。有限元模拟得到的载荷—位移曲线如图8所示。在损伤累积过程中,数值结果与实验数据[12]吻合较好,因此可以断定上述材料参数适用于任意梯度层占比的IF钢。

图8 不同梯度层占比时的轴向载荷—位移曲线Fig.8 Relationships between axial load and axial displacement for different ratio
2 应力演化分析与颈缩预测
2.1 应力状态演化
把拉伸过程分为3 个阶段:1) 材料整体处于弹性变形;2) 芯部粗晶层进入塑性变形阶段,梯度层靠近芯部的区域发生屈服,但其余部分仍处于弹性变形阶段;3) 材料全截面屈服。通过分析不同位置的等效塑性应变与轴向拉伸应变的关系,发现当轴向拉伸应变达到0.022%时芯部材料开始发生屈服,轴向应变继续增大到0.32%时全截面屈服。有限元模拟结果表明:在上述3 个变形阶段中,轴向应力σx在拉伸过程中没有特殊的变化,与均质粗晶材料拉伸时的情况完全相同;应力分量σxy,σxz趋近于零,应力分量σz,σyz尽管不为0,但是比σy小1 个数量级。因此,以下仅讨论侧向应力σy的演化。
在3 个拉伸阶段中选取4 个代表性拉伸应变,提取模型中对称截面(X=0截面)上所有材料点的σy值,结果如图9所示。由图9(a)可知:当材料整体处于弹性变形阶段时,侧向应力σy接近于0,可以认为此时试样处于单轴应力状态。当芯部粗晶发生塑性屈服时,如图9(b)所示,此时接近表面的梯度层内的σy为负值,而芯部粗晶和相邻梯度层内的σy为正值,在正负应力变换处有非常大的应力梯度。由图9(c)可知:在材料全断面屈服的初始阶段,由于梯度层的应变硬化程度较小,依然处于表面受拉芯部受压的应力状态。由图9(d)可知:进一步增大轴向拉伸应变至3.7%,此时梯度层的应变硬化程度已经非常大,应力状态发生反转,呈现出表面受压芯部受拉的应力状态,但是相对于图9(b)所示结果,应力数值显著减小。
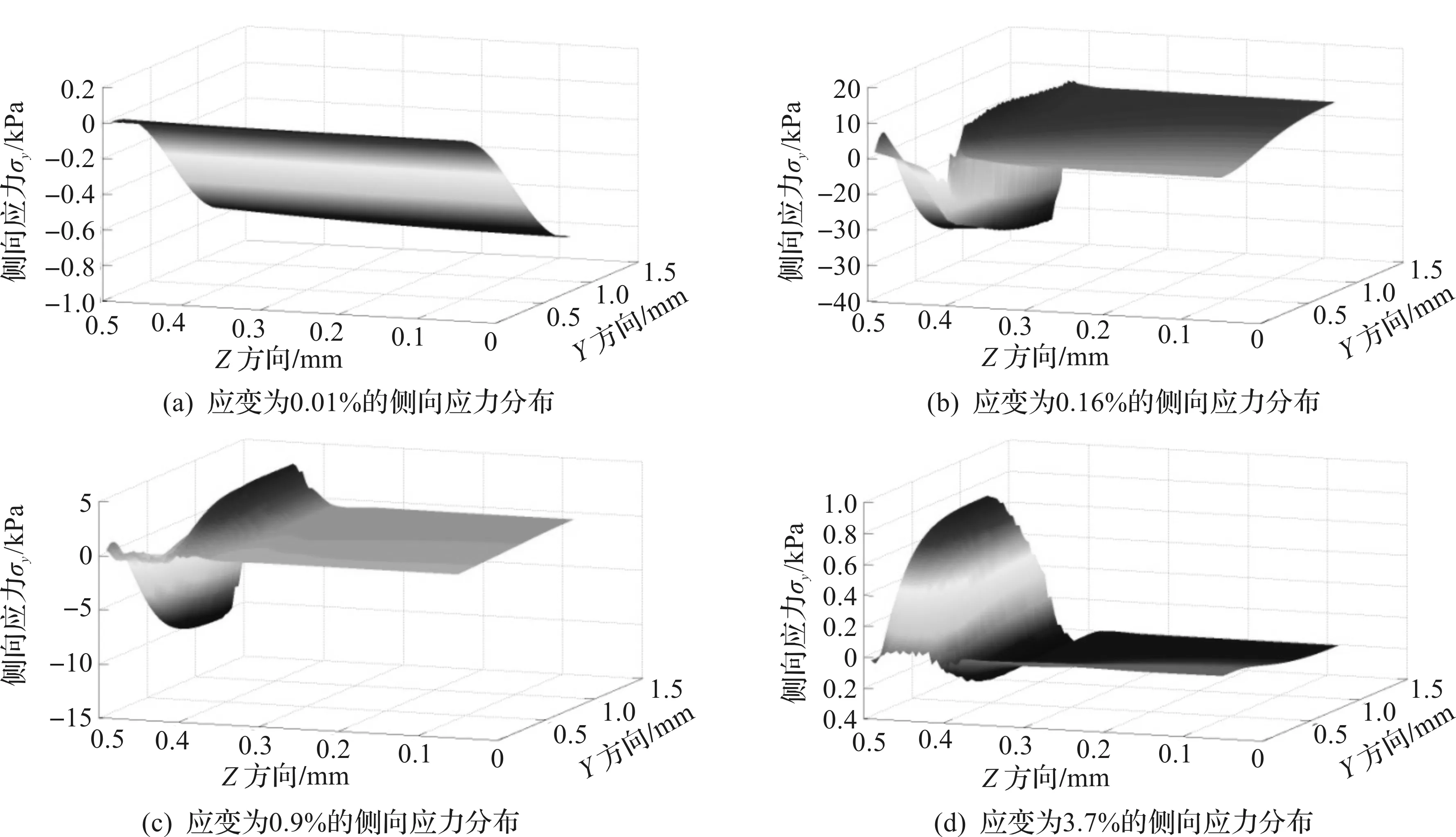
图9 不同应变下 X=0截面上σy分布Fig.9 Distribution of σy at the X=0 cross section for different strains
为了深入研究侧向应力σy随轴向应变的演化规律,提取图6中路径1上各材料点的σy值,绘制不同轴向拉伸应变下σy与深度的关系曲线,结果如图10所示。当ε<0.022%时,即材料整体处于弹性变形,σy=0。随着ε的进一步增大,芯部粗晶首先屈服,此时梯度层内的σy为负而粗晶内的σy为正,并且σy不断增大。当ε增大到0.32%时,材料全断面塑性屈服,σy达到其最大值-62 MPa。其后,随着ε增大σy逐渐减小,直至ε增加到2.1%左右时梯度层与粗晶内σy的符号反转。显然,随着轴向拉伸应变的不断增大,梯度纳米结构材料经历了如图11所示的3 种应力状态,依次为纯弹性变形时的单轴拉伸应力状态、表层受压芯部受拉的多轴应力状态和表层受拉芯部受压的多轴应力状态。

图10 侧向应力σy的演化Fig.10 Evolution of lateral stress component σy
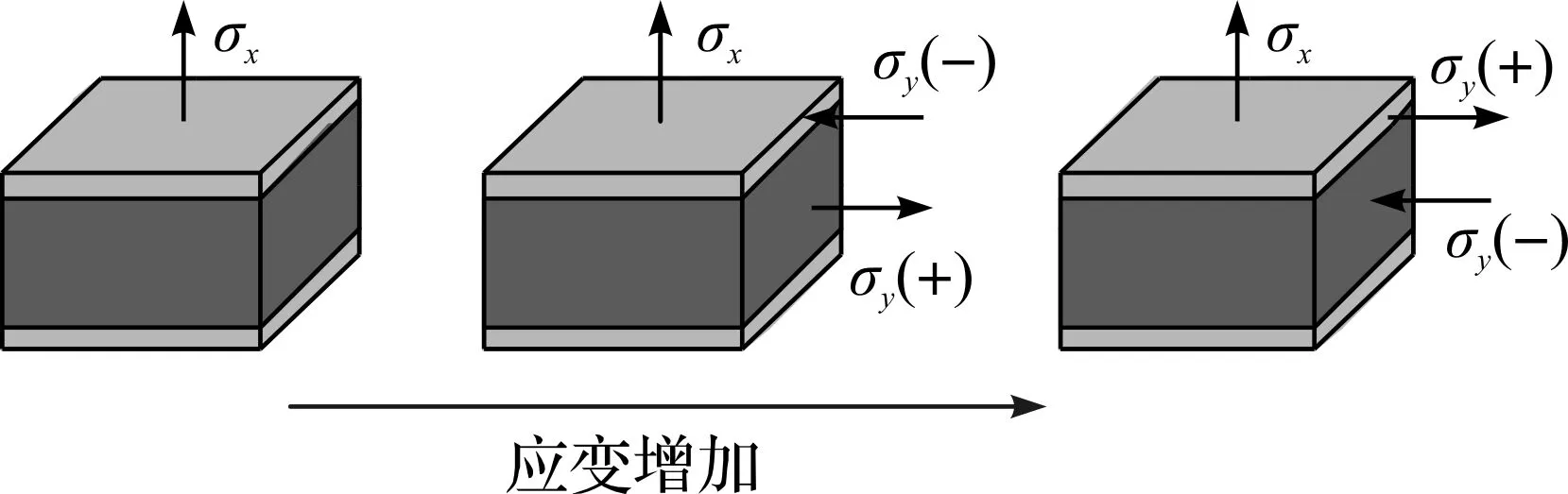
图11 梯度纳米结构材料的应力状态演化Fig.11 Evolution of stress state of gradientnanostructured material
2.2 失稳分析
梯度纳米结构材料发生颈缩时的临界应变εcr,可由Considère准则[11]进行预测为
dF/dε=0
(8)
在拉伸应变增大到εcr之前,拉力随着ε的增大而不断增大,此时dF/dε>0。当拉伸应变大于εcr以后,拉力随着ε的增大而不断减小,此时dF/dε<0。
当材料发生拉伸失稳时,轴向拉伸应变ε中弹性应变的比重极小,因此可把ε看作纯塑性应变。此时,梯度纳米结构材料的应力应变响应,可用理想刚塑性模型表示。基于式(2,6,7),可以得到轴向拉力表达式为
(9)

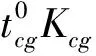
(10)
利用式(10),可以得到不同梯度层占比(16%,24%,30%)情况下的临界失稳应变,分别为0.306,0.265,0.234。
此外,基于有限元计算得到的轴向拉力—轴向应变关系曲线,利用Considère准则提取曲线中轴向拉力的最大值点,也可以方便地确定出不同梯度层占比时的临界应变。当梯度层占比为16%,24%,30%时,相应的临界失稳应变分别为0.294,0.260,0.233。两种方法确定出的结果同时绘制在图12中,显然两者具有很好的一致性。

图12 Considère准则预测的颈缩起始点Fig.12 Neck initiation predicted by considère criterion
3 结 论
基于显微硬度与流动应力的内在关系可以建立梯度纳米结构IF钢的本构模型。由模拟与实验的对比可以发现:该本构模型可以反映梯度纳米材料的协同强化效应,准确表征梯度纳米结构IF钢的拉伸力学性能。模拟结果表明:梯度纳米结构IF钢在拉伸时呈现出复杂的多轴应力状态,除了轴向拉应力外,拉伸截面上还存在变化的侧向应力。变形初期侧向应力为表面受压芯部受拉,变形增大后则演化为表面受拉芯部受压。通过有限元方法得到梯度层占比为16%,24%,30%的临界失稳应变分别为0.294,0.260,0.233,该数据与理论结果基本一致,说明了有限元模拟预测临界失稳的方法是可行的。

