空间变化模糊的图像复原算法

,

(浙江工业大学 信息工程学院,浙江 杭州 310023)

对于许多成像装置来说,它们的图像退化模型虽然可以被认为是线性的,但在图像获取传输过程中,由成像系统、传输介质方面的原因造成图像退化模型并不是空间不变(Space-invariant)的,而是空间变化的(Space-variant)。其变化性的起因主要是传输介质的非均匀性和光学系统的成像缺陷。光学系统含有像差,且像差的大小通常会随视场的变化而发生改变,而工作环境变化、系统平台振动外界因素更会加剧光学系统的像差,引起成像系统不同视场PSF的变化。除了前面两个引起空间变化的因素外,成像系统探测器响应的非均匀性,成像目标物与光学系统间的相对运动等因素也会造成系统不同视场的PSF不同。当空间不变图像复原算法用于处理空间变化产生的模糊时,其性能会下降,产生较差的恢复结果。因此需要用空间变化图像恢复模型。空间变化模型与空间不变的模型差异主要表现在:空间不变的模糊核(Point spread function)在图像退化模型中是固定不变,而空间变化的模糊核在图像的不同区域是不同的。空间变化模型,因为空间变化的特性,模糊核无法当作一个整体。从而导致空间变化模型在图像复原过程要比空间不变模型要复杂得多。在关于如何解决空间变化模糊的问题上,Costello等[1-2]提出了分块复原法,即将图像分为几块区域,每个区域的模糊核都当作空间不变的,然后使用去模糊算法复原图像后再将几个区域拼接起来形成一个完整的图像。分块复原法将复原图像块拼接后容易出现边缘效应。与之对应的是直接复原法,直接复原法中解决此类问题的一个较为普遍的方法是将模糊核用一系列基础分解矩阵来表示。Tezaur等[3-4]的一些早期的尝试,将原始模糊的子集作为分解矩阵,然后应用到图像复原算法当中。而后,Popkin等[5]开始尝试使用奇异值分解来分解模糊核。Miraut等[6]将奇异值分解模糊核运用到图像复原算法当中,提出了基于小波框架正则化的L0范数图像复原算法。Sroubek等[7]在SVD分解模糊核的基础上,使用TV范数作为正则项也取得了不错的复原效果,并横向对比了模糊核分别基于行分解的奇异值分解和基于列分解的奇异值分解的复原效果。

干净无损的图像是稀疏的,近年来基于稀疏表达的图像复原算法不断出现且取得不错的效果[8-9]。小波框架具有稀疏性和良好的局部频域特性,在图像复原中得到了很好的应用[10-12];Chan等[13]基于小波框架提出了针对空间变化模糊的高分辨率图像重建算法。近年来在压缩感知领域的一些实验表明:将TV函数和小波框架的组合作为正则项能够取得较好的复原效果[14-15]。新算法使用TV和小波框架的线性组合模型作为正则项,结合使用SVD技术将模糊核分解为一个基滤波矩阵和一个系数滤波矩阵,将正则化模型引入到空间变化去模糊领域。并运用交替方向乘子法(Alternating direction method of multipliers)对算法进行快速求解。实验表明：新的算法能够取得较好的峰值信噪比和结构相似度。

1 图像退化模型

1.1 模糊核模型

点扩散函数(PSF)描述了一个成像系统对一个点光源(物体)的响应。与空间不变产生的模糊不同,空间变化产生的模糊,它产生的PSF在图像中的每个点都是不同的。因此在图像中某点s的PSF可以用函数h(x,s)来表示,空间变化的图像退化模型可表示为

(1)

式中:u为想要恢复的清晰原始图像;g为被相机捕捉到的影像;h为模糊核函数。转化为向量矩阵的形式为g=Hu,其中H为离散空间变化模糊核的退化矩阵。

1.2 模糊核的分解

空间变化模糊核的分解有列分解(Column-wise decomposition)和行分解(Row-wise decomposition)两种形式。Miraut等[6]将模糊核表示为IKs(Integration kernels)和PSFs(Point spread functions)两种形式,IKs所对应的模糊核分解为行分解(RWD),PSFs所对应的分解形式为列分解(CWD)。通常使用PSFs来表示线性的空间变化装置要比使用IKs表达地更加自然准确,主要原因在于PSF描述了点光源在经过光学系统后,由于衍射而形成一个扩大的像点,通过测量系统的PSF,能够更准确地提取图像信息,所以PSFs要比IKs更加直观。在文献[7]中,Sroubek等使用散焦模糊来模拟空间变化模糊,并将模糊图像的模糊核分别用CWD和RWD分解方式来分解,并使用TV正则化的方法对图像进行复原。通过文献[7]的实验结果,了解到使用CWD分解法后算法恢复的图像质量要好于RWD分解法,与此同时，随着所取分解取得的奇异值个数K的增加,CWD分解法所取得的恢复图像与原始图像的均方误差(MSE)下降得更快。这表明在取得较好图像复原效果的同时减少K的值,以便于简化计算。因此,新算法采用CWD-SVD分解法来分解PSFs。

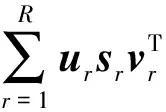
(2)

式中:sr按照从大到小排列取前k奇异值,sk=diag({σ1,…,σk})。由此可得模糊核分解公式为

(3)

式中:br(x),mr(s)分别为所需要的基滤波矩阵和系数矩阵[16]，其中br(x)=ur(x),mr(s)=srvr(s)。

结合图像退化模型,分解后,相应的图像退化模型为

g=[B1,B2,…,BK][M1,M2,…,MK]Tu+n=
BMu+n

(4)

式中:g为退化图像的向量表示;u为原始图像的向量表示;n为噪声的向量表示;B,M分别为模糊核经SVD后得到的基滤波矩阵和系数滤波矩阵。

2 图像复原算法

2.1 正则化复原模型

图像复原是一个典型的病态问题,因此需要引入原始图像的先验信息,构造附加解的先验信息作为约束条件,将病态问题良态化。这就是图像复原正则化处理的基本思想。利用正则化方法将式(4)转为求解最优化问题,求解泛函模型,即

E(u,g)=Q(u,g)+λJ(u)

(5)

(6)

2.2 基于ADMM的图像去模糊算法

为了克服TV正则化方法计算困难的缺点,近年发展出了许多高效的计算方法,如原对偶方法、FTVd、增广拉格朗日法和交替方向乘子法(ADMM)等。为了求解上述模型,将式(6)转化为约束最优化问题。ADMM算法是机器学习中比较广泛使用的约束问题最优化方法,它是增广拉格朗日法的一种延伸,其主要目的是为了弥补了二次惩罚的缺点。在一些问题中,二次惩罚来近似约束问题在最优点附近需要惩罚项的系数趋于无穷,这会使得海森矩阵很大,因此近似的目标函数会很不稳定。ADMM能够避免这种缺陷,该算法引入了线性逼近部分,通过线性系数不断的接近最优解,使得在二次惩罚项系数很小的情况下,也能得到满足要求精度的解。ADMM通过分解协调(Decomposition-coordination)过程,将大的全局问题分解为多个较小、较容易求解的局部子问题,并通过协调子问题的解而得到大的全局问题的解,所以新算法选用该方法求解模型。约束最优化问题为

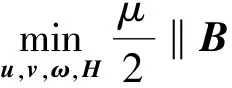
(7)

s.t.ω=Mu,v=Cu,H=Wu

将式(7)改为增广拉格朗日形式,得到

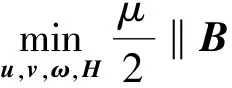
(8)

根据ADMM迭代求解算法,可以对式(8)变量进行分离求解,将式(8)转化为分别对u,ω,v,H迭代求解问题。具体迭代求解算法为

(9)

要求解式(9)的变量u,ω,v,H,只需在对应项关于变量求导为零即可,即求解极小值问题。式(9)中的第1项是关于u求导,可得

(γMTM+βCTC+ρWTW)u=γMT(ω+q)+
βCT(v+p)+ρWT(H+t)

(10)

要求解式(10),需要求出(γMTM+βCTC+ρWTW)-1。W为紧小波框架分解算子,从而有WTW=I。C为差分算子,CTC为拉普拉斯算子矩阵,因此后2项都可以在频域中快速计算,然而MTM

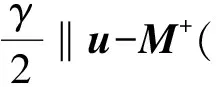
(11)

式(11)中：F和F-1分别代表傅里叶变换和傅里叶反变换。通过以上公式对变量的分离求解,再将其置入迭代优化便可以在迭代中求解u。直到在迭代过程中迭代停止准则小于已设定好的阈值或者超出最大设定迭代次数时,停止迭代。

3 仿真分析

新算法使用峰值信噪比(PSNR)和结构相似度(SSIM)来评估图像复原效果,辅以主观视觉效果的主观评价。自然图像具有极高的结构性,表现在图像的像素间存在着很强的相关性,这些相关性在视觉场景中携带着关于物体结构的重要信息。SSIM能够使图像和参考图像的结构比较失真。相较于传统所使用的影像品质衡量指标,结构相似性在影像品质的衡量上更能符合人眼对影像品质的判断。PSNR值越大,SSIM的值越接近于1,说明恢复图像越接近原图像,恢复效果越好。

实验原始图像分别选取分辨率为256×256的“Lena”“Cameraman”“House”“Barbara”图像。实验编程环境为Matlab2016b。实验需要添加空间变化模糊,因其特殊性,退化模型采用文献[7]提供的散焦模糊来获取退化图像。即假设模糊核函数已知,模糊程度可改变参数来手动控制。而在实际应用中,模糊核需要被估计出来才能进行图像的复原。设置最大迭代次数为500。

新算法添加的模糊与文献[7]相同,因此将新算法与文献[7]所提出的TV复原模型进行比较,对比算法参数取原值。部分实验结果如图1～3所示。其中图1(a)为原始清晰的图像“Lena”,图1(b)为添加散焦模糊后的图像,图1(c)为用文献[7]算法复原的图像,图1(d)为新算法复原的图像。图2(a)和图3(a)中为原始图像,图2(b)和图3(b)为模糊图像,图2(c)和图3(c)为新算法复原图像。图4为实验图1(b)新算法与文献[7]算法的迭代次数与PSNR值的关系图,图5为实验测试图“Lena”在不同模糊程度下(PSF变化速率值越大,模糊程度越高),新方法和文献[7]算法复原图像PSNR值的对比数据图。更多实验数据对比结果如表1所示。

图1 “Lena”模糊图像复原结果Fig.1 The result of blurred image “Lena”

图2 “Barbara”模糊图像复原结果Fig.2 The result of blurred image “Barbara”

图3 “Cameraman”模糊图像复原结果Fig.3 The result of blurred image “Cameraman”

图4 文献[7]与新算法PSNR随迭代次数对比Fig.4 PSNR comparison between proposed method and reference[7] with iteration number

图5 文献[7]与新算法PSNR随模糊程度的对比Fig.5 PSNR comparison between proposed method and reference[7] with speed of PSF changes

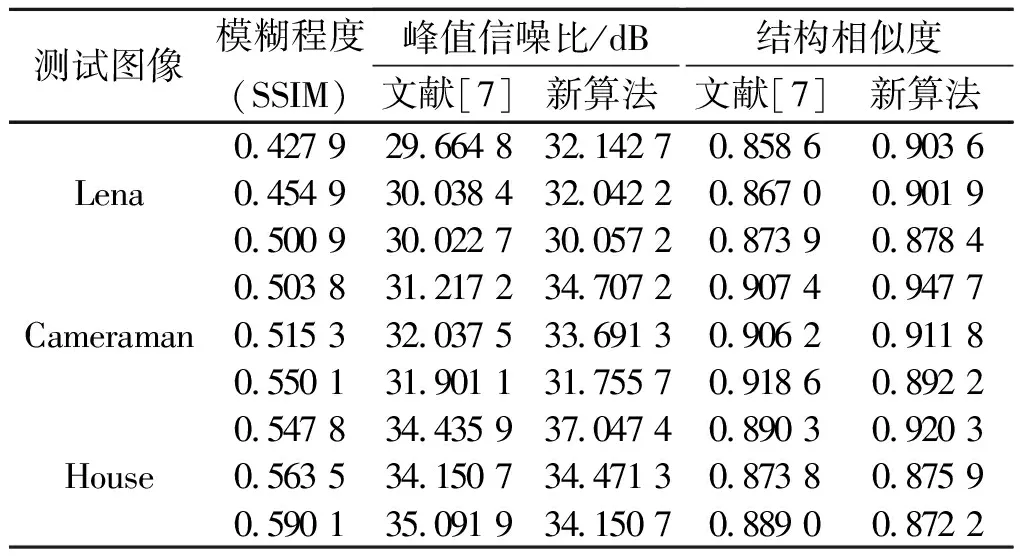
测试图像模糊程度(SSIM)峰值信噪比/dB文献[7]新算法结构相似度文献[7]新算法LenaCameramanHouse0.427 929.664 832.142 70.858 60.903 60.454 930.038 432.042 20.867 00.901 90.500 930.022 730.057 20.873 90.878 40.503 831.217 234.707 20.907 40.947 70.515 332.037 533.691 30.906 20.911 80.550 131.901 131.755 70.918 60.892 20.547 834.435 937.047 40.890 30.920 30.563 534.150 734.471 30.873 80.875 90.590 135.091 934.150 70.889 00.872 2

从图1(c,d)的对比,可以看出新算法复原的图像在发丝、帽檐纹理较多的区域比文献[7]算法复原的图像要更加清晰,而图4也可以表明,新算法在迭代次数230之前效果差于对比算法,但随着迭代次数的增加,新算法的复原效果要好于对比算法。表1“lena”图像的第一行数据也表明,迭代最终结果新算法在PSNR上比文献[7]算法产生的结果高出2.47 dB左右,在SSIM数值上要高出0.045左右。在表1的实验中,具体的对比了3幅经典图像在不同模糊程度下,新算法与文献[7]算法的复原效果。每幅测试图像的模糊程度,由上至下模糊程度越来越低(SSIM越高)。从实验结果可以看出,新算法提出的结合TV和小波框架的双正则化模型的复原效果在PSNR和SSIM都略优于文献[7]提出的正则化恢复模型的复原效果。图5的数据显示,相比于文献[7]算法,在测试图像模糊程度较低时,新算法表现不太理想,产生的复原效果与对比算法持平甚至略低,但随着原始图像模糊程度的增加,新算法的最终复原效果越加明显。新算法通过增加了小波框架作为先验信息,每次迭代的计算量略有增加,但基本与文献[7]相当,结合以上图表数据显示出的去模糊效果,当添加的模糊程度越深,新算法取得的恢复结果更加优于文献[7]算法的恢复结果。

在实际例子中,模糊图像恢复需要先计算模糊核参数,得到参数之后再使用图像复原算法进行恢复。新算法未涉及到模糊核参数的估计,故无法在模糊核参数未知的情况下对图像进行复原。图6(a)是一幅车辆在行驶过程中拍下的图像,由于相机曝光时间过长或者车速过快等原因,导致图中车牌模糊不清。将模糊图像使用算法[3]对其模糊核参数进行估计,可以得到相关的模糊中心、长度、方向等信息。再将估计好的模糊核参数代入到算法中进行复。对比图6(a,b)两幅图像,车牌号由原始的模糊不清经过算法复原之后变得清晰可见。

图6 模糊图像的复原Fig.6 Restoration of fuzzy images

4 结 论

TV正则化和小波正则化图像复原算法是近年来效果较好、效率较高的算法。针对在空间变化模糊中图像恢复的问题,传统复原算法表现效果不佳。新算法基于模糊核分解,结合传统正则化技术,提出一种总变分和小波框架双正则化模型。并使用ADMM算法将原问题分解为易于求解的子问题进行独立求解,使得算法能快速迭代收敛。实验结果表明,新算法提出的方法在图像去模糊恢复过程中能够较好地保存原始图像的边缘信息和细节。同其他算法相比,新算法取得了更好的客观评价指标,在主观上也具有更好的视觉效果。