改进的软件缺陷预测模型研究

,,

(浙江工业大学 信息工程学院，浙江 杭州 310023)

随着智能工具不断发展，软件的更新迭代越来越频繁，软件缺陷[1]预测问题也受到社会的广泛关注。比如2009年出现的Gmail故障，由于测试小组遗漏了一个软件缺陷，造成了极大的损失和不便，因此有效地预测软件缺陷模块成为亟待解决的问题。而应用机器学习的软件缺陷预测模型能够尽早地预测和发现软件缺陷，保证软件质量，减小损失，是一种高效的软件缺陷预测手段。软件缺陷问题也属于不平衡数据[2-4]问题。软件缺陷只存在于小部分软件模块中，缺陷模块数量远小于正常模块数量。目前应用在软件缺陷预测模型中的算法主要有支持向量机[5-8](Support vector machine，SVM)、朴素贝叶斯算法[9](Naive bayes，NB)、人工神经网络[10]和马尔可夫链[11]等，结合SVM的改进算法存在泛化能力不足的问题，结合朴素贝叶斯的改进算法由于朴素贝叶斯假定特征向量的各个分量独立地作用于决策变量而同样存在泛化能力不足的问题，结合人工神经网络的改进算法存在容易陷入局部最优和网络结构需要多次调整的问题。

为了提高软件缺陷模型的准确性，提出了改进的软件缺陷预测模型(FREDSVM)。即采用改进的频繁项集挖掘算法(IMMFIA)[12]来获取频繁项集，具有低时间复杂度和空间复杂度的特点；在具有相同前件的所有规则中选择相关度最大的规则，利用新的规则排序度量(RSS)对规则进行排序，得到分类器；针对规则匹配无果(对于不能被分类器中的规则所满足的测试样例)和规则匹配溢出(对于有多个规则满足测试样例的情况)问题，结合EDSVM[13]进行分类。

1 相关工作

1.1 改进的关联分类算法

1.1.1 改进的频繁项集挖掘算法(IMMFIA)

马丽生等提出的IMMFIA算法在FP-tree[12-14]基础上，对其结构进行修改，减少了FP-tree分支重复遍历的次数，同时利用剪枝策略和压缩策略缩小搜索空间和压缩FP-tree的规模，降低了时间复杂度和空间复杂度。

1.1.2 相关度和排序规则强度(RSS)

设Q为元组的数据集合，Q中每个元组用n个属性R1,R2,…,Rn和一个类标号属性Rc描述。项k为一个形如(Ri,v)的属性-值对，其中Ri为属性，取值v。项的集合称为项集，满足最小支持度阈值的项集称为频繁项集。支持度和置信度是关联分类[15-16]算法中的重要概念，分别衡量关联规则的重要性和正确率。

规则A⟹B的支持度s为

s(A⟹B)=P(A⟹B)

(1)

规则A⟹B的置信度c为

c(A⟹B)=P(B|A)

(2)

规则R:A⟹B的规则强度[17]SS(A⟹Bi)为

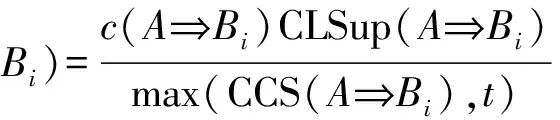
(3)

规则的类支持度CLSup为

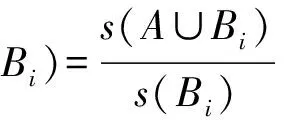
(4)

规则的补类支持度CCS为

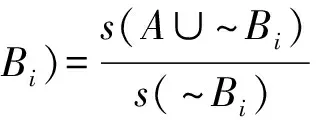
(5)

式中：s(A∪～Bi)为规则补类的支持度；s(～Bi)为类Bi的补类支持度。

1.2 EDSVM算法

1.2.1SVM算法

支持向量机方法(Support vector machine，SVM)借助于最优化方法来解决机器学习问题的工具，逐渐成为克服“维数灾难”和过拟合等问题的有效手段。定义是根据给定的训练集，即

T={(x1,y1),(x2,y2),…,
(xl,yl)}∈(X×Y)l

(6)

式中：xi∈X=Rn，X称为输入空间，输入空间中的每一个点xi由n个属性特征组成；yi∈{-1,1},i=1,2,…,l。寻找Rn上的一个实值函数g(x)，以便用分类函数f(x)=sgn(g(x))，推断任意一个模式x相对应的y值的问题为分类问题。当样例线性不可分时，可以尝试使用核函数来将特征映射到高维。核函数可以形式化定义为：如果原始特征内积是，映射后为<φ(x),φ(z)>，那么核函数(Kernels)为

K(x,z)=φ(x)Tφ(z)

(7)

SVM对复杂的非线性边界的建模能力较强，尽管训练较慢，但是分类结果非常准确，且不容易过拟合，使得SVM算法在许多领域被广泛应用。

1.2.2 KNN算法

KNN[18-20]算法又称K-最近邻分类算法(K-nearest-neighbor-classifier)，该算法的基本思路是：如果一个样本在特征空间中的K个最近邻的样本中的大多数样本属于1个类别，则该样本也属于这个类别。该算法主要涉及3个量：训练集、距离或相似的度量、K的大小。该算法简单、易于实现，属于懒惰算法，需要扫描全部样本计算，计算量大、速度较慢和内存消耗较大，而且受K值影响严重:若K值太小，则分类获得的有效信息少，甚至丢失；若K值太大，则包含较多其他类别的点，精度降低。

1.2.3 EDSVM算法

王超学等[13]提出的EDSVM算法的基本思想是：当测试样例与SVM分离超平面之间的距离q大于一定值d时，采用SVM算法进行分类；否则以所有的支持向量作为测试样例的近邻样本，进行KNN 分类。EDSVM算法充分利用支持向量能够代表训练数据集的含义，同时，使得KNN 算法降低对近邻参数的依赖，有利于提高分类器的分类精度。

2 软件缺陷测试模型的建立

基于FREDSVM建立软件缺陷预测模型，主要步骤如图1所示。

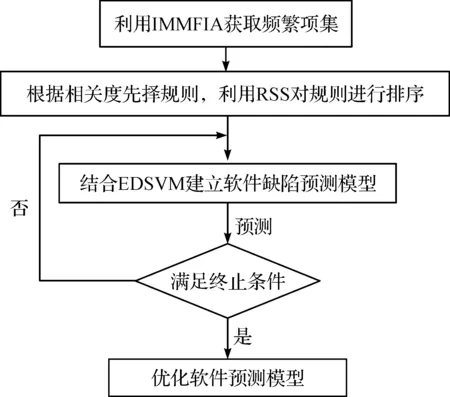
图1 基于FREDSVM建立软件缺陷预测模型流程图Fig.1 The flow chart of establishing software defect prediction model based on FREDSVM

2.1 构造分类器

获取数据集之后，利用IMMFIA来获取频繁项集，它具有低时间复杂度和空间复杂度的特点，分析频繁项集，产生每个类的满足置信度和支持度阈值的关联规则，结合相关度，在具有相同前件的所有规则中选择相关度最大的规则，利用RSS对规则进行排序，得到分类器。得到分类器之后，便可以对测试样例进行分类预测。

规则R:(A⟹Bi)的相关度[21]CL为

CL(A⟹Bi)=c(A⟹Bi)-s(Bi)

(8)

规则R:A⟹Bi的排序规则强度为

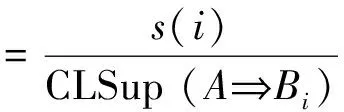
(9)

由CL和RSS 可以看出：小类规则的置信度和支持度较小，但是两者相减之后的数值与大类的置信度和支持度相减的数值相差不大，所以在具有相同前件的所有规则中选择相关度最大的规则，可以有效提高小类的匹配概率；利用RSS 对规则进行排序，同样可以有效提高小类的优先级，弱化不平衡数据集带来的问题，从而提高分类准确性。

2.2 结合EDSVM进行分类预测

传统的关联分类算法在进行分类预测的时候通常存在两种情况：1) 对于不能被分类器中的规则所满足的测试样例(规则匹配无果)，分类器具有一个最低优先级的默认规则，自动为其指定默认规则，例如CBA[22]就把规则集中具有最大置信度的规则指定给测试样例；2) 对于有多个规则满足测试样例的情况(规则匹配溢出)。

针对不平衡数据而言，上述两种做法的分类精度并不理想，可能会出现小类规则无法分类或者分类错误的情况。在出现规则匹配无果和规则匹配溢出情况时，结合EDSVM进行分类预测能达到“因材施教”的效果。当规则匹配无果时，在除去规则集的训练集中采样EDSVM算法进行分类预测，即当测试样例与SVM分离超平面之间的距离q1大于一定值d时，采用SVM算法进行分类；否则以所有的支持向量作为测试样例的近邻样本，进行KNN 分类；当规则匹配溢出时，在规则集中采样EDSVM算法进行分类预测，即当测试样例与SVM分离超平面之间的距离q2大于一定值d时，采用SVM算法进行分类；否则以所有的支持向量作为测试样例的近邻样本，进行KNN 分类。具体算法步骤如下：

输入测试样例T，训练集Q，规则集R，除去规则集的训练样本ExpR，常量d。

输出测试样例的类别。

步骤1在规则集R中找出满足测试样例T的m个规则。

步骤2若选出的m个规则相同，则测试样例的类别即为该规则的类别，输出结束。

步骤3若选出的m个规则相异，则判断是规则匹配无果还是规则匹配溢出，规则匹配无果跳转步骤4，规则匹配溢出跳转步骤5。

步骤4若规则匹配无果，则在除去规则集R的训练集Q中计算测试样例与SVM分离超平面之间的距离q1，若q1>d，则采用SVM算法进行分类，否则以所有的支持向量作为测试样例的近邻样本，进行KNN分类。

步骤5若规则匹配溢出，则在规则集R中计算测试样例与SVM分离超平面之间的距离q2，若q2>d，采用SVM算法进行分类，否则以所有的支持向量作为测试样例的近邻样本，进行KNN分类。

步骤6输出测试样例的类别。

3 改进的软件缺陷预测模型实验

3.1 评估性能度量

采用混淆矩阵作为评估性能度量，如表1所示。

表1 混淆矩阵1)Table 1 Confusion matrix

注：1)TP表示被分类器正确分类的正类数；TN表示被分类器正确分类的负类数；FN表示被分类器错误分类的负类数；FP表示被分类器错误分类的正类数。

传统的分类算法一般采用准确率，即

(10)

作为评估性能度量。针对不平衡数据集，该度量不够合理。因为准确率偏向于反映大类的分类情况而忽略了小类的分类情况，可能会导致错误判断了分类器的分类预测效果。因此，采用F值(调和平均值)和准确率指标共同作为评估性能度量。

精度为

(11)

召回率为

(12)

F值为

(13)

3.2 实验数据

NASAMDP(Metrics data program)是由美国航空航天局发布的专门用于构建软件缺陷预测模型的公开数据集，是实验最常用的数据。采用4个公开数据集JM1，KC1，PC1和CM1进行实验，数据集具体分布情况如表2所示。

表2 实验数据Table 2 Experimental data

表2中，数据集中字段Defective值为Y的模块属于有缺陷的模块，否则为无缺陷的模块，计算出缺陷率。因为数据集中存在部分冗余的属性，所以要对数据集进行数据预处理操作，只取其中有用的属性，如表3所示。

表3 数据集属性Table 3 Attribute of datasets

3.3 实验结果与分析

图2中的4张子图分别为LR，SVM，ACO-SVM以及提出的方法FREDSVM在JM1，KC1，PC1和CM1数据集上的测试结果。从图2中可以看出：LR与SVM这两种方法预测结果受数据集影响较大，在JM1和PC1数据集上，SVM测试效果优于LR，而在KC1和CM1数据集上，LR较优，这是由于LR受数据容量的限制，而SVM则受限于调参；ACO-SVM方法不仅克服了数据容量的局限，还优化了SVM调参受限的问题，所以测试效果优于LR和SVM；FREDSVM利用IMMFIA获取频繁项集，再根据RSS提高小类的优先级，然后运用EDSVM针对规则匹配无果和规则匹配溢出问题进行分类，得到的测试结果优于LR，SVM及ACO-SVM方法。

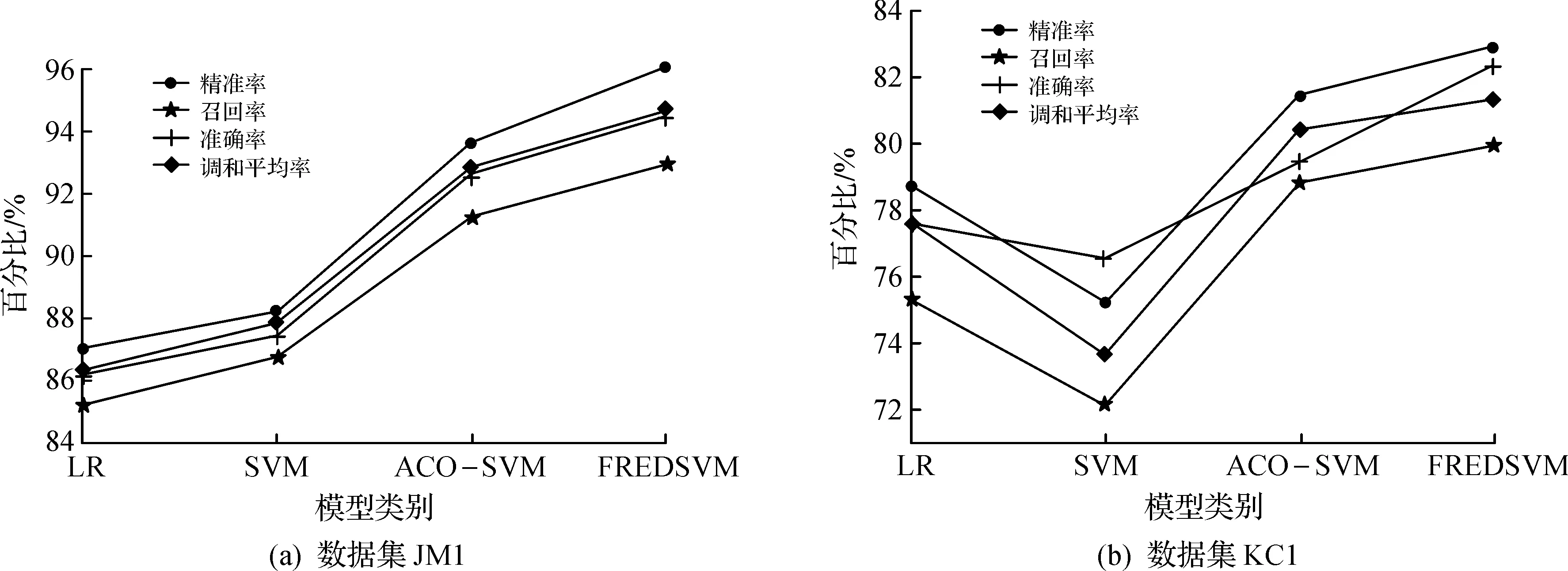
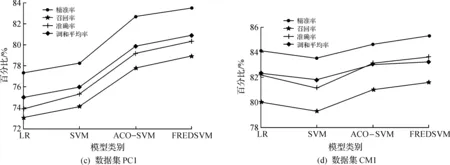
图2 数据集预测结果对比Fig.2 Comparison of forecasting results in datasets

4 结 论

针对软件缺陷预测模型的准确性问题，提出了改进的软件缺陷预测模型(FREDSVM)。主要思想是将利用IMMFIA获取到的频繁项集根据相关度和新的规则排序度量RSS进行排序，提高小类的优先级，然后运用EDSVM针对规则匹配无果和规则匹配溢出问题进行分类。通过对LR，SVM，ACO-SVM以及FREDSVM算法在JM1，KC1，PC1和CM1数据集上测试对比分析，结果表明：FREDSVM比传统的软件缺陷预测模型效果更优，在相同数据集上具有更高的精确率和召回率。在运用EDSVM进行分类时，针对SVM的调参问题在今后可以进行优化。