身管火炮膛压和最大射程落点诸元与初速关系经验拟合公式

孟 程，王雨时，张志彪，闻 泉，王光宇

(南京理工大学机械工程学院，江苏 南京 210094)

0 引言

火炮、弹丸型号和发射装药确定之后，弹丸的炮口初速就可以确定了。然而目前已有的弹道诸元参数计算公式多为需要较多参数的、复杂的时间函数式。文献[1—3]中列出了真空弹道中弹道诸元参数与时间的关系式，但很少有文献研究身管火炮膛压和最大射程落点诸元与初速之间的关系，文献[4]仅给出了比较复杂且计算参数较多的经验公式。因此针对特定弹炮系统，根据已有弹道数据进行内弹道、外弹道特性参量之间函数关系定量分析，给出简洁的适用于引信和战斗部设计的弹道诸元与炮口初速的函数关系经验公式就十分必要。在引信和战斗部总体论证、初步设计甚至是在初步摸底试验时，弹丸射程、飞行时间、落角、落速等弹道诸元参数数值信息往往不全，因而给性能、质量分析和试验数据评估与鉴别带来一定困难。本文针对上述问题，提出了应用1stOpt软件以有多号发射装药的155 mm加榴炮普通榴弹、122 mm榴弹炮普通榴弹和120 mm迫击炮弹为例，对内、外弹道学运动方程简化分析的方法。

1 拟合软件介绍及拟合算例

1.1 拟合软件

1stOpt(First Optimization)是我国七维高科有限公司独立开发的一套数学优化分析综合工具软件包，主要用于非线性回归、曲线拟合、非线性复杂模型参数估算求解、线性/非线性规划等领域。1stOpt软件不仅操作界面简单，而且其核心计算方法——通用全局优化算法(UGO,Universal Global Optimization)克服了当今世界上在优化计算领域使用迭代法必须给出合适初始值的难题，即不需要用户给出参数初始值，在绝大多数情况下，仅依靠自身的全局搜索能力，从任意随机值出发，就可求得最优解[5]。

1.2 拟合算例

以155 mm加榴炮普通榴弹为算例，已知数据如表1和表2所列。已知身管长lg=7.046 m。其中各装药号下的初速V0、最大膛压Pm、最大射程Xm是由射表给定的，落速Vc、全飞行时间T以及最大射程角θ0、对应最大射程角的落角θc则由弹丸外弹道质心运动方程反推出弹道系数c43后计算得出。

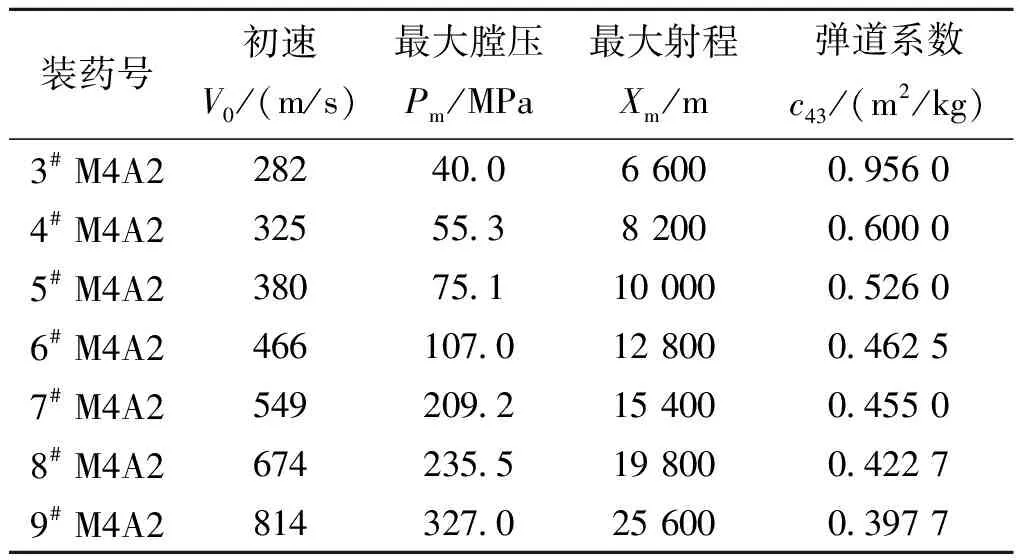
表1 155 mm加榴炮普通榴弹射表给定的弹道诸元和反求得到的弹道系数

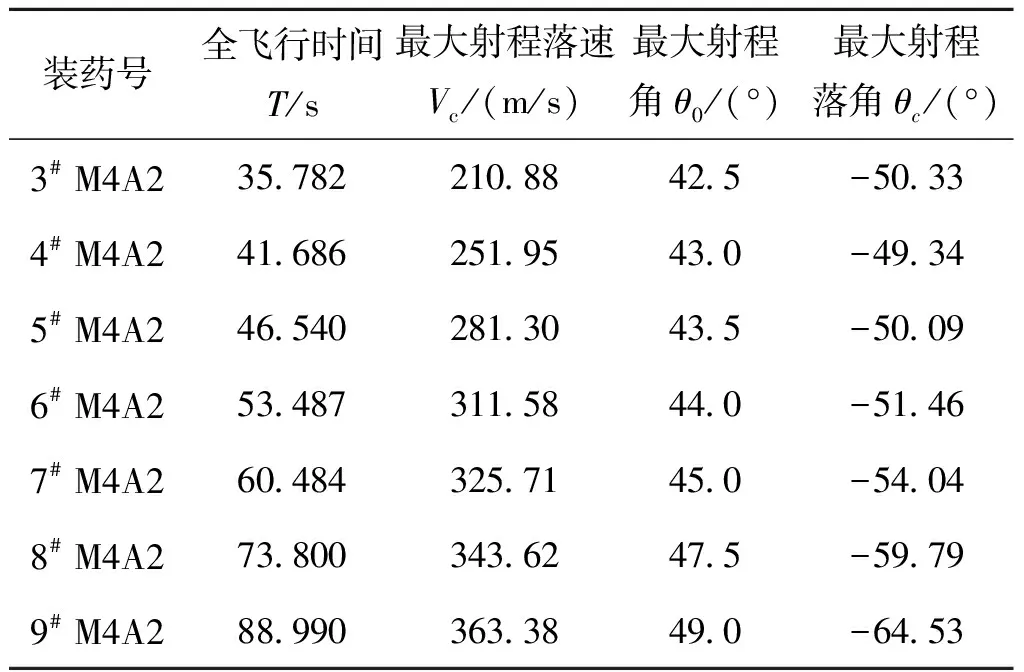
表2 155 mm加榴炮普通榴弹外弹道诸元解算结果

2 身管火炮膛压和最大射程落点诸元与初速关系经验拟合

2.1 身管火炮最大膛压与弹丸初速关系拟合

在内弹道中，膛内最大压力位置不是在炮口处，但最大膛压可以由膛内平均膛压估算得出[6]，由在简化假设基础上的内弹道方程组可知[7]：

(1)

式(1)中，S为炮膛横截面积，P为膛内平均压力，φ为次要功计算系数，m为弹丸质量，v为弹丸在膛内的瞬时速度，t为弹丸在膛内的时间。可以看出，该方程中，只要火炮和弹丸型号确定，S、φ、m就为已知量，将弹丸的瞬时速度和时间进行积分可以得出：

(2)

(3)

(4)

因此，最大膛压和弹丸初速关系式为：

(5)

由上式可知，最大膛压与弹丸初速是最高二次幂的关系。应用1stOpt软件进行拟合，为了提高拟合曲线的精度，选用的拟合公式形式为：

Pm=b0+b1V0+b2V02+b3V03+b4V04

(6)

经过拟合发现使用1stOpt拟合时公式中的常数项b0不为0而且数值较大，这是由此软件具有较高的拟合精度造成的。如果弹丸在炮口没有速度但是最大膛压存在，说明弹丸在膛内的摩擦导致弹丸达到炮口时速度减小到0，这在实际工程中是有可能存在的。由于实际弹丸速度较高，所以为了简化起见，可以假设b0值为0，由此得：

Pm=-0.274 23V0+0.001 807V02-1.534 6×
10-6V03+4.060 1×10-10V04

(7)

式(7)中，Pm的计量单位为MPa，V0的计量单位为m/s。拟合后的曲线如图1所示。

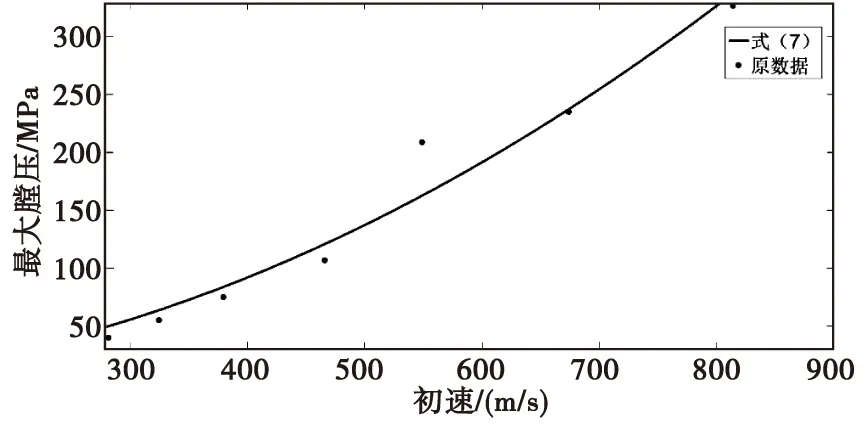
图1 拟合后的火炮最大膛压与弹丸初速关系曲线Fig.1 Relationship curve between the maximum chamber pressure of artillery and the initial velocity of projectile after fitting

拟合后的公式中，虽然b3、b4的值很小，但是也对拟合结果有影响。将b3、b4取为0后再进行拟合，拟合后：

Pm=0.051 21V0+4.478×10-4V02

(8)

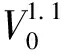
(9)

由于理论计算时最大膛压与初速为二次幂的关系，因此再分别拟合一条一次幂关系的直线和二次幂关系的抛物线，同式(9)进行比较。直线和抛物线公式分别为：

Pm=0.329 5V0

(10)

Pm=5.230 5×10-4V02

(11)

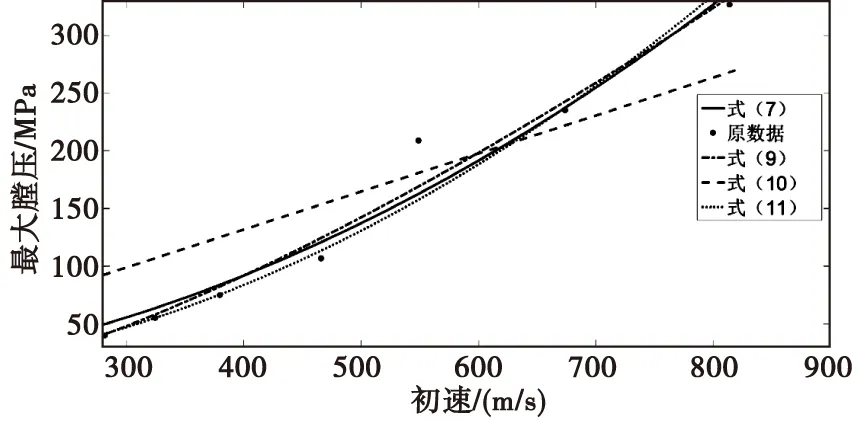
图2 拟合后的火炮最大膛压与弹丸初速关系曲线Fig.2 Relationship curve between the maximum chamber pressure of artillery and the initial velocity of projectile after fitting

对比上述的拟合结果可发现，拟合后式(7)、式(9)、式(11)与原数据符合度较好，式(10)与原数据差距较大，在式(7)、式(9)、式(11)中以式(11)最简洁，而且与理论计算最为符合，故拟合后火炮最大膛压与初速平方成正比。式(8)至式(11)中Pm的计量单位为MPa，V0的计量单位为m/s。

2.2 身管火炮最大射程与初速关系拟合

在空气弹道中射程与弹丸初速的关系为[4]：

(12)

式(12)中：

(13)

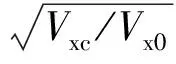
Xm=b1V0+b2V0a

(14)

经过改变a的取值，可以得到当a=1.6时，拟合公式的均方差最小，拟合后：

Xm=16.427 4V0+0.266 9V01.6

(15)

Xm的计量单位为m，V0的计量单位为m/s。为了使公式简化，再拟合出一条直线：

Xm=28.971 9V0

(16)

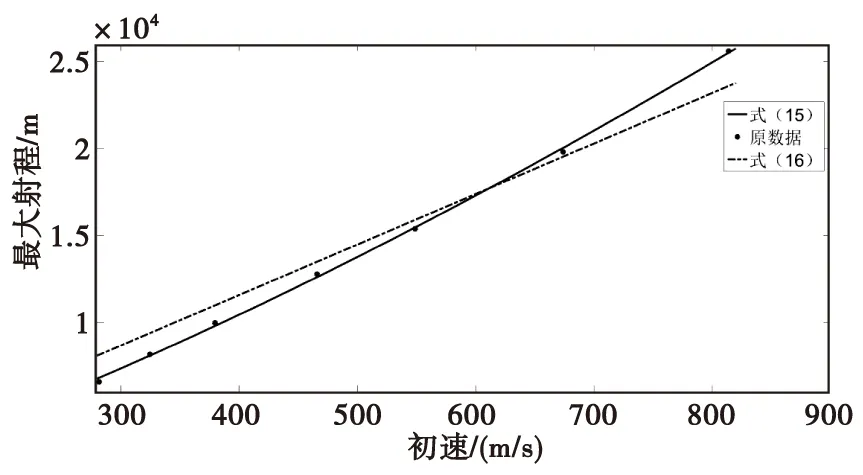
图3 拟合后的火炮最大射程与弹丸初速关系曲线Fig.3 Relationship curve between the maximum range of artillery and the initial velocity of projectile after fitting

对比原数据与式(15)、式(16)的拟合结果可以观察到式(16)较为简洁，故拟合后火炮最大射程和弹丸初速近似呈线性关系。

2.3 身管火炮最大射程落速与初速关系拟合

在空气弹道中，落速受到外弹道环境的影响与射程受到的影响一样，因而[4]：

(17)

式(17)中，Vxc=Vccosθc，Vx0=V0cosθ0。

化简可得：

(18)

从上式可知，火炮落速与弹丸初速、射角、落角有关。通过简单的计算可以发现，弹丸的射角和落角的余弦函数值的比值是逐渐减小的，线型大致为抛物线，因而选择的射程和弹丸初速之间的拟合关系式为：

Vc=b1V0a+b2

(19)

拟合后：

(20)

式(20)中，V0和Vc的计量单位均为m/s。

在式(20)中，如果弹丸落速为0，弹丸初速经过计算也约等于0，与理论分析结果一致。拟合后的公式均方差很小，相关系数接近于1，说明在本文算例的初速范围内弹丸落速与初速的拟合公式是可信的。拟合后弹丸落速与弹丸初速的关系曲线近似为抛物线，初速无限增大，落速趋于恒值374.5 m/s。

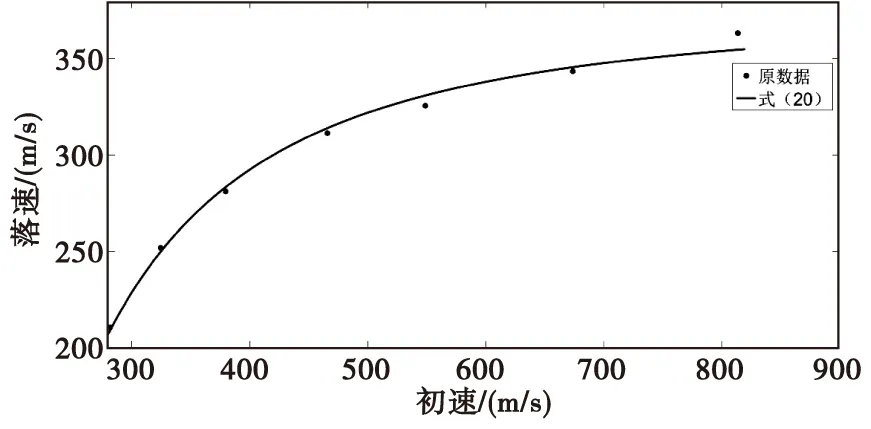
图4 拟合后的弹丸最大射程落速与弹丸初速关系曲线Fig.4 Relationship curve between the falling velocity of maximum range of artillery and the initial velocity of projectile after fitting

2.4 身管火炮弹丸全飞行时间与初速关系拟合

在空气弹道中，弹丸飞行时间受到外弹道环境的影响，因而[4]：

(21)

将公式化简可得：

(22)

从上式可知，弹丸飞行时间与弹丸初速、射角、落角和空气阻力系数有关，通过以上公式简单计算可知，弹丸全飞行时间与初速大致为一次幂关系，因而选用的拟合关系式为：

T=b1V0+b2V0a

(23)

拟合后：

T=0.284 8V0-9.077 5×10-2V01.1

(24)

式中，T单位为s，V0单位为m/s。再对式(21)进一步简化：

T=0.112 8V0

(25)

将式(23)、式(24)与原数据相比较可以得到式(25)较为简洁，误差也在允许的范围内，这表明弹丸飞行时间与弹丸初速近似呈线性关系。

2.5 身管火炮最大射程落角与初速关系拟合

在空气弹道中，由于受到外弹道阻力的影响，落角的绝对值肯定会比射角大。目前未见到有弹丸落角与弹丸初速之间的关系，因而使用1stOpt软件自带的自动搜索匹配公式的功能进行拟合，经过分析比对选用的拟合公式为：

θc=b0+b1V01.5+b2V02.5+b3V03

(26)

拟合后的关系式为：

θc=-62.759+6.826×10-3V01.5-
2.387×10-5V02.5+5.392×10-7V03

(27)

图5 拟合后的弹丸全飞行时间与弹丸初速关系曲线Fig.5 Relationship curve between the full flight time of artillery and the initial velocity of projectile after fitting

观察原数据的图形可以发现，原数据与逻辑斯蒂曲线形状相似，再以逻辑斯蒂曲线公式进行拟合，可以得到：

(28)

由于逻辑斯蒂曲线形状较为线性，再拟合出一条一次幂关系的直线：

θc=-2.884 6×10-2V0-39.844 1

(29)

式(27)—式(29)中，θc的计量单位为(°)，V0的计量单位为m/s。

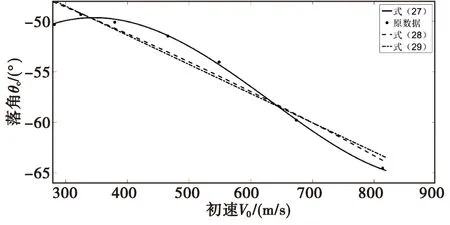
图6 拟合后的弹丸最大射程落角与弹丸初速关系曲线Fig.6 Relationship curve between the falling angle of maximum range of artillery and the initial velocity of projectile after fitting

对比式(27)、式(28)、式(29)的拟合结果，可以观察到式(27)与原数据符合程度较高。但是在误差允许的范围内，式(29)更为简洁，拟合后弹丸落角与弹丸初速近似呈线性关系，初速越大，落角绝对值也就越大。

2.6 122 mm榴弹炮普通榴弹与120 mm迫击炮弹最大射程落点诸元与初速关系

为了验证拟合关系式的普适性，再选用122 mm榴弹炮普通榴弹与某120 mm迫击炮弹最大射程落点诸元与初速的数据进行拟合。其中拟合某120 mm迫击炮弹最大射程落点诸元与初速关系时，试验数据较少不足以进行拟合，因而将已知的试验数据反求得的弹道系数取平均值后解算不同初速下的弹道诸元，求得的弹道系数平均值为0.788 5。拟合所需的参数如表3、表4[8]、表5和表6所示。

经过拟合可以得到122 mm榴弹炮普通榴弹的最大射程、最大射程落速、全飞行时间和最大射程落角与弹丸初速的拟合关系式为：

Xm1=23.923 0V01

(30)

(31)

T1=0.067 4V01+19.200 2

(32)

θc1=-0.025 8V01-41.929 5

(33)

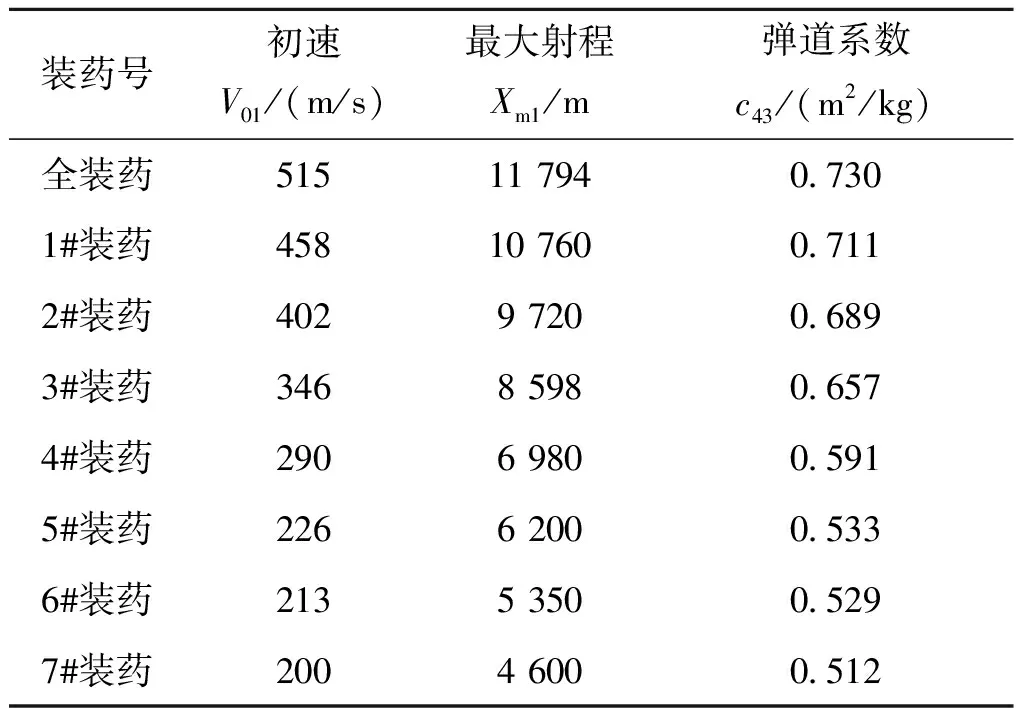
表3 122 mm榴弹炮普通榴弹射表给定的弹道诸元和反求得到的弹道系数

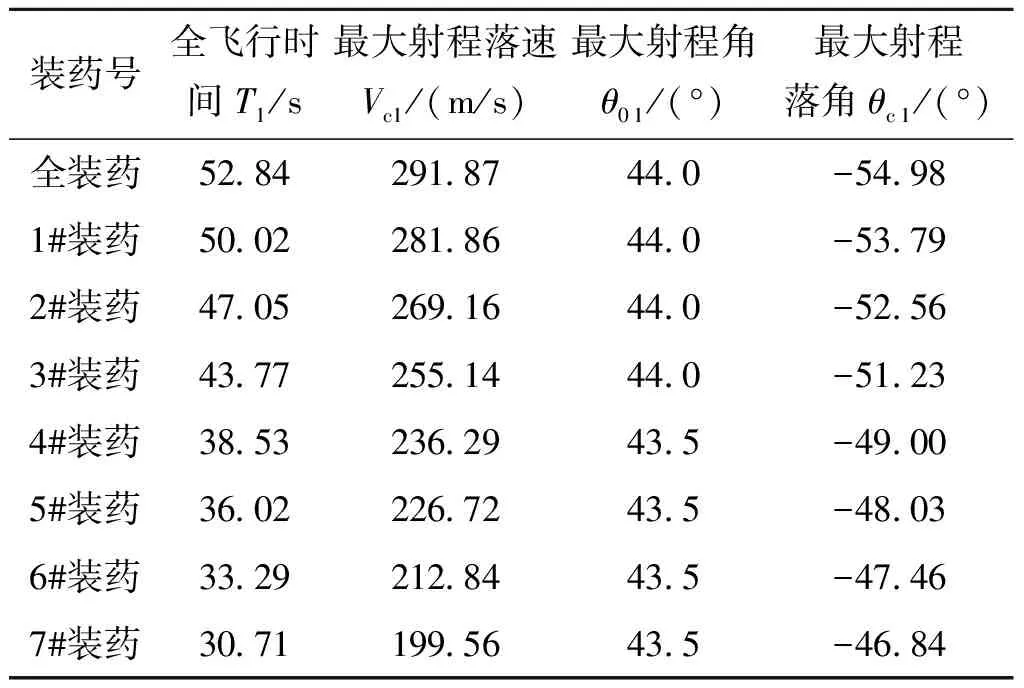
表4 122 mm榴弹炮普通榴弹外弹道诸元解算结果

表5 120 mm迫击炮弹已知的初速、解算使用的弹道系数和最大射程

表6 120 mm迫击炮弹外弹道诸元解算结果

某120 mm迫击炮弹的最大射程、最大射程落速、全飞行时间和最大射程落角与弹丸初速的拟合关系式为：

Xm2=30.615 3V02-2 416.338 2

(34)

Vc2=-1.608 8×106V02-2+232.289 5

(35)

T2=0.117 3V02+3.183 1

(36)

θc2=-0.022 0V02-43.614 2

(37)

3 分析与讨论

各个公式的相对误差如表7、表8和表9所列。

由于要求拟合关系式尽量简洁直观，所以所选拟合公式并不是误差最小的。

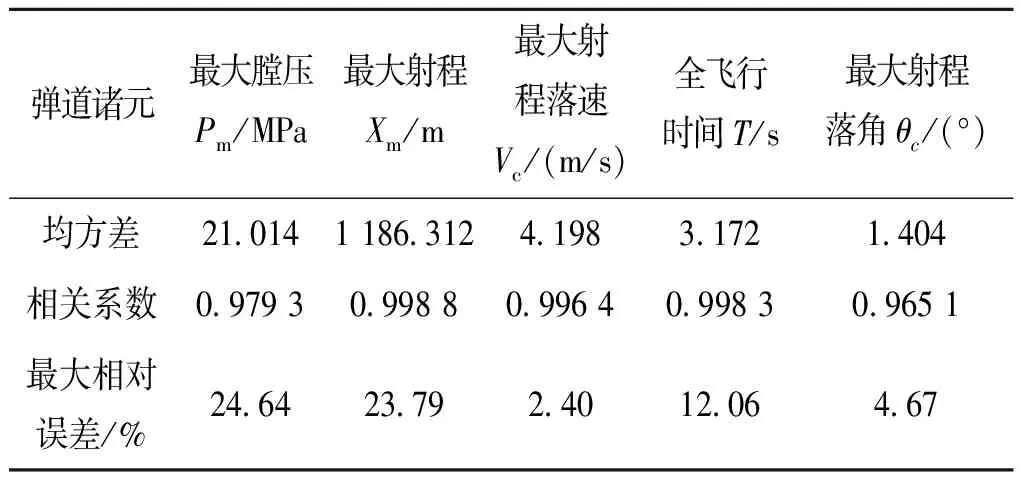
表7 155 mm加榴炮普通榴弹拟合后的公式与原数据的相对误差

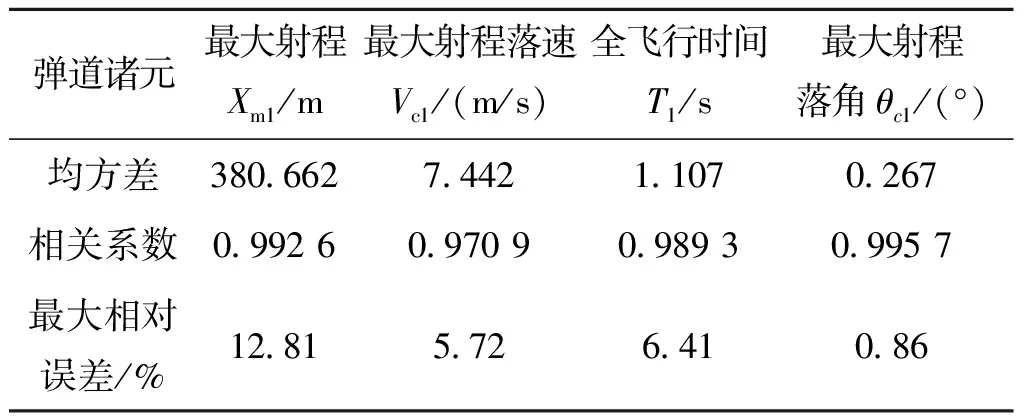
表8 122 mm榴弹炮普通榴弹拟合后的公式与原数据的相对误差

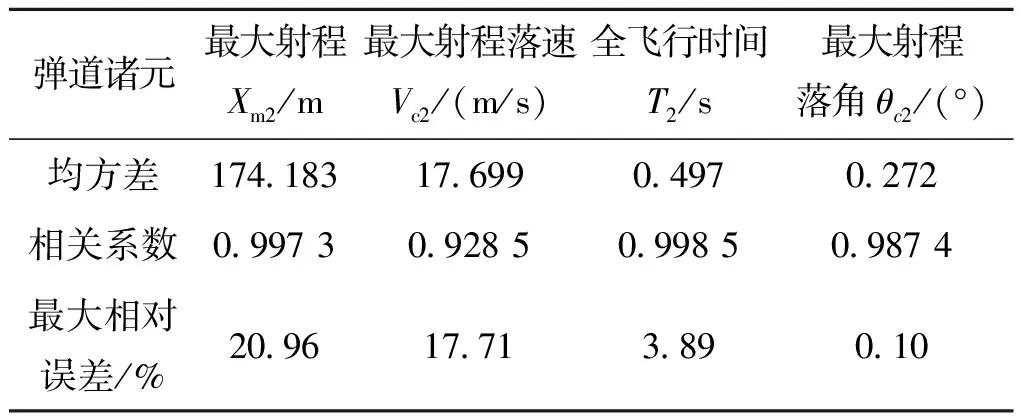
表9 120 mm迫击炮弹拟合后的公式与原数据的相对误差

从表7至表9可知，最大膛压、最大射程和最大射程落速与弹丸初速拟合公式的最大相对误差均较大。在拟合过程中，修改初速指数，可得到不同的拟合公式。降低初速指数，可使拟合公式更为简洁，从而便于揭示出清晰的规律。由于各种火炮的空气弹道规律大体上是相同的，所以本文虽然只是针对三种火炮进行计算对比，但是所得基本规律对于其他火炮同样适用，应该具有普适性，有助于弹药和引信总体论证、初步设计、性能分析和试验评估时的外弹道特性估算参考。对于其他火炮弹药系统，只要有对应不同初速的最大膛压和最大射程落点诸元数据，就可以按本文的方法拟合出身管火炮诸元如膛压(影响引信发射过载系数)和最大射程落点诸元与初速之间的关系(规律)。

4 结论

本文提出了应用1stOpt软件以有多号发射装药的155 mm加榴炮普通榴弹、122 mm榴弹炮普通榴弹和120 mm迫击炮弹为例，对内、外弹道学运动方程简化分析的方法。该方法基于对155 mm身管火炮普通榴弹弹道诸元与初速关系进行分析，拟合了弹道诸元中最大膛压、最大射程、最大射程时的落速、全飞行时间、最大射程时的落角与初速之间的函数关系，利用这个函数关系可以迅速得到弹道诸元的近似值。拟合结果表明：最大膛压与初速平方近似呈正比；最大射程及全飞行时间与初速近似呈正比；最大射程落速与初速的关系曲线近似为抛物线，初速无限增大，最大射程、落速趋于恒定值；最大射程落角与初速近似呈线性关系，初速越大，落角也越大。