基于模糊滑模变结构的工业机械臂控制系统研究

郑晓斌

(福建船政交通职业学院 机械工程系， 福建 福州 350007)

工业机械臂是一个末端能动机械装置，属于工业机器人的一个重要分支，其运动任务可包括焊接、油漆、组装、绘图等，广泛应用于装备制造、产品加工、机器作业等关键领域。工业机械臂系统是一种典型的高精度位置/速度跟踪伺服系统，具有时变、强耦合和非线性的动力学特征，在低速运行时，摩擦力成为影响系统动态品质的重要因素，它不但造成系统的稳态误差，而且使系统产生爬行、振荡。

从控制的角度来说，针对摩擦环节引起的问题，周海晶[1]用滑模控制方法，通过设计两个滑动模面，实现了带有一个弹性力臂的两关节机器人控制。刘强等[2]提出了一种新的指数型滑模超平面，加快了系统沿着滑模面的收敛速度。苗红[3]利用滑模控制中的切换函数作为模糊系统的输入，设计了单输入模糊控制器(Fuzzy Controller，FC)，提高了滑模控制的跟踪速度。

本文采用一种模糊滑模变结构控制器，控制信号由滑模变结构控制器产生的滑模等效控制量和由模糊控制器产生的切换控制量组成，使抖动得到最大程度地削弱，同时还能保持系统有较强的鲁棒性。

1 机械臂伺服系统数学模型的建立

1.1 机械臂伺服系统描述

机械臂中采用的高精度位置直流伺服系统均为三环结构，即在双闭环调速系统的基础上，附加位置环，组成“电流—速度—位置”控制系统。当该系统采用直流电机、忽略电枢电感、电流环和速度环为开路时，可简化成为一个线性二阶系统，伺服系统位置状态方程可描述为[1]

(1)

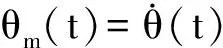
1.2 机械臂伺服系统摩擦模型

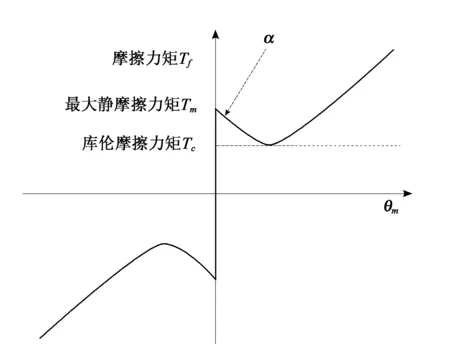
图1 摩擦-转速稳态关系曲线(Stribeck曲线)

在所有的运动中摩擦均以不同的形式存在，特别对有高精度、高性能要求的伺服系统影响尤为突出[4]。在机械臂位置运动伺服系统中，运动速度为零时，静摩擦使系统相应表现存在“死区”特性，系统响应存在多个平衡点，从而使得系统存在很大的静态误差；当系统的速度穿越零点时，静摩擦可能会使系统出现“平顶”现象；当系统处于低速运行情况下，系统会出现静、动、静、动……的跳跃运动，即低速爬行现象[2]。

Stribeck曲线是比较著名的摩擦模型，如图1所示，该图表明了在摩擦的不同阶段，转速与摩擦力矩之间的关系。本文机械臂伺服系统采用Stribeck摩擦模型进行建模，其数学表达式如下：

当|θm(t)|<α时，静摩擦为

(2)

(3)

当|θm(t)|≥α时，动摩擦为

Tf(t)=[Tc+(Tm-Tc)e-α1|θm(t)|]sgn(θm(t))+kvθm(t)，

(4)

式中T(t)是驱动力矩，Tc是库仑摩擦力矩，Tm是最大静摩擦力矩，kv为粘性摩擦力矩系数，θm(t)为转速，α和α1为正常数。

2 模糊滑模变结构控制技术应用的提出

目前机械臂伺服系统控制中应用最广的控制策略是PD控制，通过调节PD控制器的参数，能减小系统超调，克服震荡，从而提高系统的稳定性，加快系统过渡过程，提高系统的静态性能。当机械臂低速运行的时候，摩擦力起主导作用，其具有显著的非线性运动特性；当运行速度穿越零点时，位置跟踪曲线会发生变形，采用常规的PD控制器不能达到理想的控制效果[5]。

近年，模糊逻辑控制和滑模变结构控制等现代控制理论在运动控制领域倍受青睐，模糊逻辑控制无需精确的传递函数，算法较简单，执行速度也较快；滑模变结构控制对外界干扰以及系统参数变化的影响不明显，能驱动系统按预定的路径进行动作，具有响应及时、高精度、高稳定性、鲁棒性强等优点[3]。本文把常规的滑模变结构控制和模糊控制结合，构建一种新的复合控制策略，即模糊滑模控制(Fuzzy Sliding Mode Control，FSMC)，如图2机械臂伺服系统模糊滑模变结构控制结构框图所示，图中虚框部分为模糊滑模控制器，其输出控制量由滑模变结构控制器的输出ueq和模糊控制器(FC)的输出us组成。模糊滑模控制器与对象数学模型的依赖程度小，同时又可以有效地减少常规滑模变结构控制的抖振现象[1,6]。

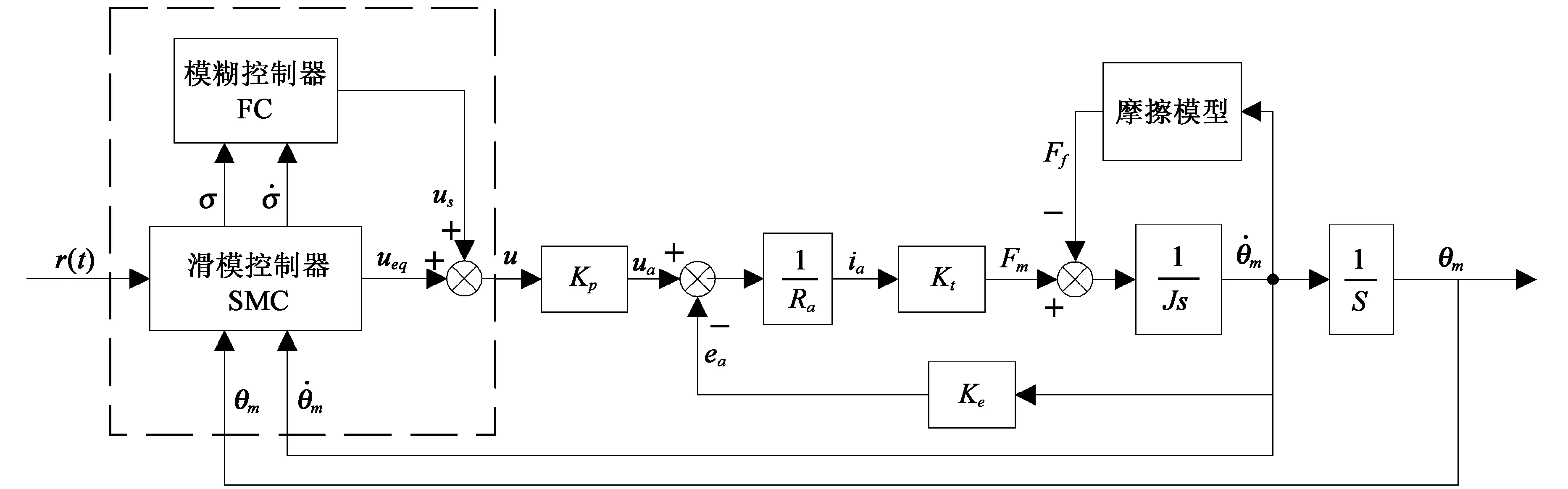
图2 机械臂伺服系统模糊滑模变结构控制结构框图

3 模糊滑模变结构控制器的设计

3.1 滑模控制器的设计

模糊滑模控制算法采用滑模等效控制法，输出控制量分别由滑模变结构控制器(SMC)的输出ueq和模糊控制器(FC)的输出us组成，可将控制量u设计为

u=ueq+us，

(5)

式中：ueq为滑模等效控制量，将系统状态保持在切换面上而始终不离开切换面；us为切换控制量，用来补偿估计误差，迫使系统状态在滑模面上滑动。

设计滑模变结构控制的切换函数为

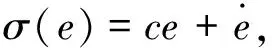
(6)

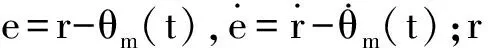
根据滑模控制的等效控制条件dσ/dt=0和Tf=0，由式(1)和式(6)可推导出滑模变结构的等效控制[3]：

(7)

3.2 模糊滑模控制器的设计

一般滑模变结构控制器u是通过设计切换函数和设计趋近律(如等速趋近律、指数趋近律等)来直接设计。通过选用合适的趋近律的方法来改善趋近运动的动态品质，但机械臂伺服系统在低速运行过程中，控制力的不连续切换以及实际控制中的时间和空间的滞后，系统难免会产生爬行和抖动现象。本系统采用模糊控制器(FC)，通过模糊推理和反模糊化直接求解切换控制量us，使抖动得到最大程度地削弱，同时还能保持系统有较强的鲁棒性。

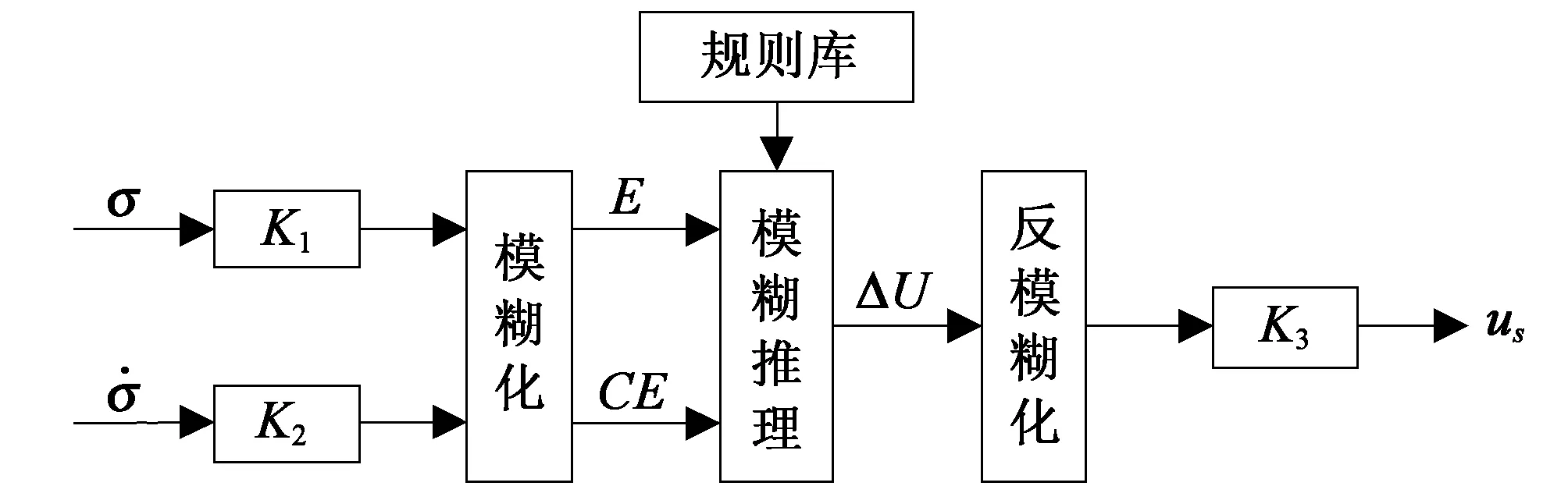
图3 模糊控制器(FC)的结构图

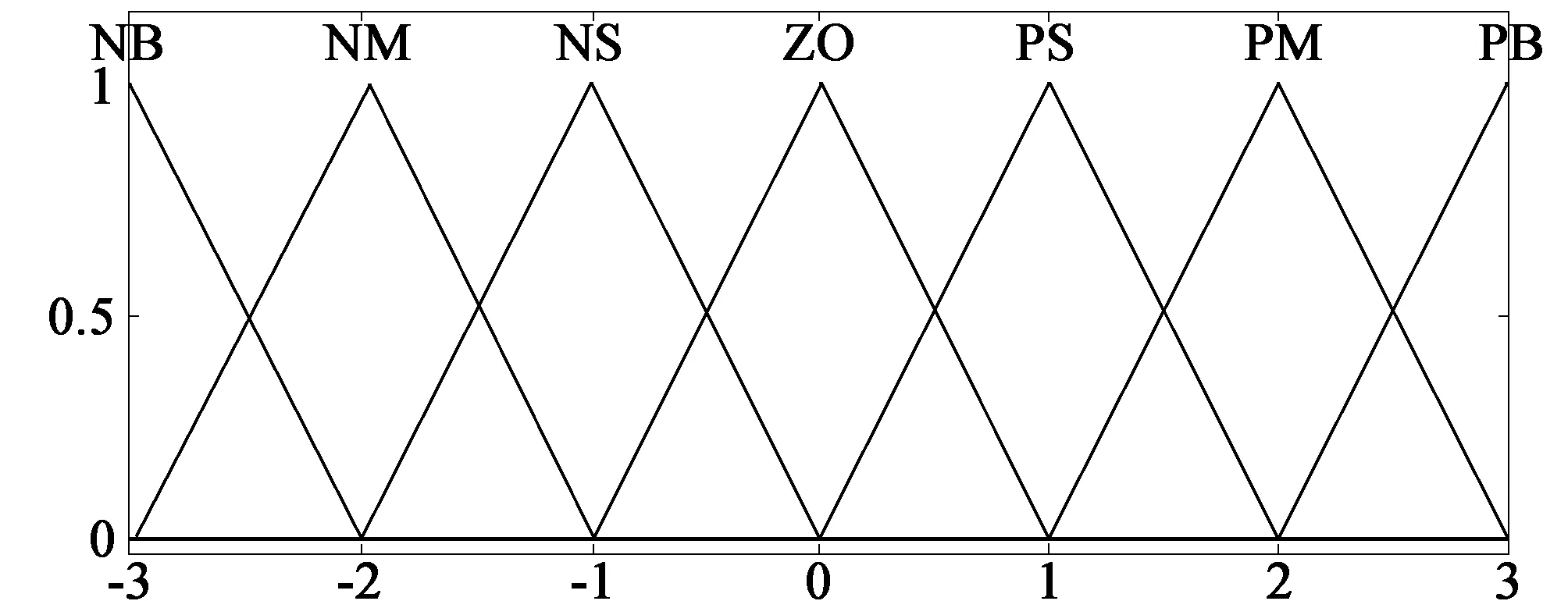
图4 E、CE和ΔU的隶属度函数

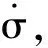
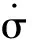
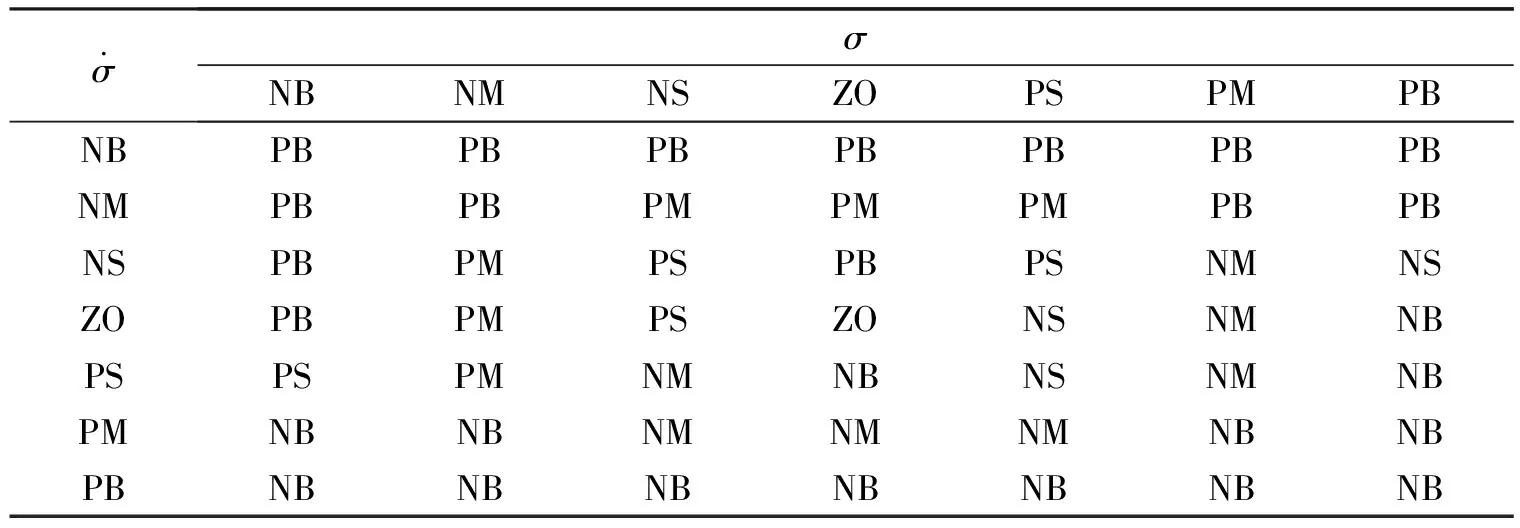
表1 ΔU的模糊控制规则表

为了获得准确的控制量，本文输出结果采用面积重心法(即加权平均法)[9]，它是根据最终模糊推理计算结果和输出隶属度函数运算所得到的图形的重心U′作为ΔU输出的精确值，从而得到切换控制量us，即

us(i)=K3[Uo+U′(ΔU，μu)]，

(8)

其中：Uo为模糊控制器输出的初始值；ΔU为模糊推理计算值；μu为模糊输出隶属函数的隶属度；K3为输出变量比例因子；us为模糊控制器输出值，也是滑模控制器切换控制量。

4 系统仿真分析

为了验证所构建的模糊滑模变结构算法在工业机械臂驱动系统中的控制效果，利用MATLAB/Simulink软件对系统进行仿真运行，来分析控制策略的控制性能以达到最佳控制效果。基于模糊滑模变结构的工业机械臂驱动控制系统仿真模型如图5所示[3,7]。

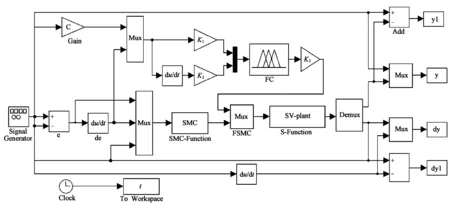
图5 模糊滑模变结构的工业机械臂驱动控制系统仿真模型

系统中的机械臂伺服电机的参数和模糊滑模变结构控制器的参数为：电枢回路总电阻Ra=12.12 Ω，电动机的力矩系数Kt=9 N·m/A，电压反馈系数Ke=1.8 V/(rad/s)，放大器倍数Kp=15，转动惯量J=1.1 kg·m2，最大静摩擦力矩Tm=20 N·m，库仑摩擦力矩Tc=16 N·m，粘性摩擦力矩比例系数kv=2.8 N·m·s/rad，α=0.01，α1=1，控制系统位置给定信号r(t)=0.15sin(πt)；滑模变结构切换系数c=20，输入输出变量的量化因子K1=12、K2=50、K3=10。

将伺服系统的传递函数和摩擦模型函数均采用M文件的形式编写在SV_plant中，并设置系统的初始位置为-0.3。为了分析模糊滑模变结构控制器的性能，将其与常规的PD控制器(关闭FC通道，在SMC控制器中采用PD控制，Kp=100，Kd=10)和滑模变结构控制器(采用指数趋近律直接求u，同时关闭FC通道)的位置跟踪曲线进行比较，仿真结果如图6—图9所示[5,12]。

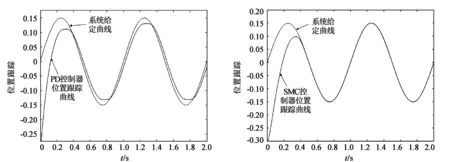
图6 PD控制器位置跟踪 图7 SMC控制器位置跟踪

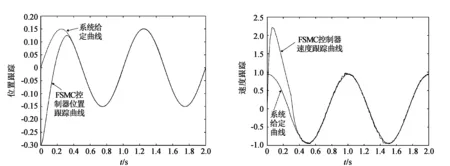
图8 FSMC控制器位置跟踪 图9 FSMC控制器速度跟踪

如图6所示，机械臂伺服系统在摩擦干扰条件下运行时，PD控制器输出的位置跟踪曲线响应均始终不同程度滞后于目标曲线，同时存在较明显的“平顶”现象，第一个波峰时的位置跟踪曲线峰值为0.11，与系统给定的0.15相比误差达到26.6%，鲁棒性能差，抗干扰能力弱，无法实现高精度的跟踪运行。如图7所示，采用基于趋近律的常规滑模变结构SMC控制器，系统输出从第二个波峰起位置跟踪精度有明显的提高，已无“平顶”现象，但启动瞬间的动态效果还不如PD控制器，第一个波峰时(峰值0.1)与系统给定的误差高达33.3%；同时系统启动响应不及时，需经过0.45 s才能最终捕捉跟踪到目标曲线。从图8、图9中可以分析得到，采用模糊滑模变结构FSMC控制器，不仅能够很好地消除摩擦造成的“平顶”现象，抗干扰性较强，响应快，启动瞬间第一个波峰(峰值0.125)时与系统给定的误差率约为13.3%，而且过渡时间明显小于前者，只需要0.3 s就能实现系统从静到动的跟踪，启动跟踪响应时间缩短了50%，速度跟踪振荡现象也得到明显的抑制。

5 结 论

本研究将模糊控制与滑模变结构算法相结合应用于工业机械臂伺服驱动系统中，该算法不仅可以简化滑模等效控制量的求解，而且可通过模糊推理和反模糊化求解切换控制量，来代替需通过选择趋近律进行设计的传统滑模变结构控制器。仿真结果表明，该控制策略既不依赖于系统精确的数学模型，同时还能简化控制系统结构复杂性的作用，具有良好的动态性能和稳态性能，具有响应速度快、鲁棒性强的特点，弥补了传统PD控制和滑模变结构控制在机械臂伺服驱动中所存在的不足，改善了系统的动、静态性能，为高精度工业机械臂运动控制系统的整体开发提供了重要的参考价值。