自适应广义形态滤波和GG聚类在轴承故障识别中的应用研究
季云健, 黄国勇, 黄刚劲
(昆明理工大学 信息工程与自动化学院, 云南 昆明 650500;云南省矿物管道输送工程技术研究中心, 云南 昆明 650500)
滚动轴承是旋转机械设备中最重要的元件之一,机械部件的故障很大程度上是由轴承故障所引起的[1]。轴承从正常运转到发生故障的过程实质上是一个渐变的过程,故障发生的初期往往故障特征不明显且易被噪声淹没而不易被发现,加之不同故障类型有一定的相似度,导致提取到的特征具有模糊性,直接通过提取到的特征进行故障类型识别的准确率较低。鉴于此,如何在复杂的工业生产环境下对滚动轴承类型进行准确的分类与识别,具有十分重要的工程研究价值。
Huang等[2]通过经验模态分解(Empirical Mode Decomposition,EMD)方法对信号自适应分解,得到一系列频率成分由高到低的固有模态(Intrinsic Mode Function,IMF)分量,并得到了广泛应用,但在分解的过程中会存在端点效应和模态混叠现象。针对此问题,Wu等[3]通过高斯白噪声均匀分布的统计特性提出了总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD),有效地抑制了模态混叠现象,但人为添加的白噪声不能完全中和,会存在虚假分量,进而导致故障诊断的误判。在此基础上,Gang Y等[4]提出了变模式分解(Variational Mode Decomposition,VMD),较大程度地减少了EEMD重构信号中的残余白噪声。胥永刚等[5]通过双树复小波包变换结合支持向量机(Support Vector Machine,SVM)对滚动轴承故障振动信号进行故障诊断。任学平等[6]提出了小波包最优熵结合相关向量机的故障诊断方法。胡荣华等[7]提出经验模式分解与改进的免疫参数自适应支持向量机相结合的滚动轴承故障智能诊断方法。上述文献将一系列模式识别的方法用在了故障诊断上,有效识别出故障类型,但这些方法过分依赖于知识库现有知识,当新的故障特征出现时,无法准确识别。
本文提出一种基于自适应广义形态滤波和GG聚类故障诊断方法。首先采用自适应广义形态滤波对轴承振动信号进行降噪处理,然后对降噪后的信号进行VMD分解,去除虚假分量和噪声分量;对去噪后故障特征较多的信号分量求解近似熵,作为特征向量输入GG聚类分类器中来诊断滚动轴承故障。
1 自适应广义形态学基本理论
1.1 广义形态滤波基本理论
由于形态平均算子在级联过程中采用相同结构元素进行滤波,并没有完全消除正负脉冲噪声的干扰,存在输出统计的偏倚现象。因此采用后级结构元素大于前级结构元素的方法来构造开-闭和闭-开的广义形态滤波器[8],不仅可以有效地消除了输出偏倚问题,而且可以抑制正负脉冲噪声的干扰,达到了良好的降噪效果。在实际应用中,广义形态滤波器存在采用加权系数选取的不确定性的问题,仍然会存在输出偏移现象,导致对滚动轴承振动信号降噪效果并不理想。为解决此问题,采用文献[9]LMS算法处理权系数的确定问题,即构建自适应广义形态滤波。
1.2 自适应广义形态滤波器的构建
令某待测信号为x(n)=s0(n)+d(n),其中s0(n)为理想信号,d(n)为噪声信号。则误差信号为
e(n)=s(n)-y(n),
(1)
其中y(n)为滤波输出信号,s(n)为期望响应。
滤波输出信号为
(2)
其中ai(n)为权系数。
输出信号的均方差为
(3)
通过LMS算法,取单个误差样本平方e2(n)作为均方误差E[e2(n)]的估计,并对权系数求导。通过最陡坡下降法优化权系数,最终可得:
ai(n+1)=ai(n)+2μyi(n)e(n),i=1,2,
(4)
式中μ为控制收敛速度的参数。
2 信号分解和特征提取
2.1 VMD分解方法
VMD分解具有自适应、准正交、完备性等特点。该分解方法能够一次性地将多分量分解成单分量,也可认为VMD法使信号分解问题变成约束最优化问题,所得最优解即为所分解出来的单分量,且在解决模式混叠问题上,效果明显优于EEMD、EMD。因此本文选择VMD分解。VMD算法详细过程见参考文献[10]。
2.2 近似熵
近似熵具有强抗噪性、适合处理随机信号等优点。鉴于时间序列越复杂对应的近似熵值越大,可用该值来反应旋转机械设备在不同工况下振动信号的复杂程度。
近似熵求解具体步骤如下所示[11]:
Step1:提取时间序列{x(1),x(2),…,x(N)}中m个元素,构建矢量X(i);
Step2:定义矢量X(i)与X(j)之间的最大距离d[X(i),X(j)];
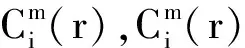
Step5:将维数m加1,变成m+1,重复步骤step1—step4可得到Φm+1(r);
但在实际情况中N的值为有限值,根据步骤step1—step6可得到序列长度为N时ApEn的值约为ApEn(m,r,N)=Φm(r)-Φm+1(r)。ApEn值与m、r、N有密切相关,数据长度N在[500,1000]内取值,嵌入维数m=2,相似容限r取0.1~0.25倍的序列标准差[12]。
3 GG聚类算法
聚类分析方法是目前模式识别方法中最流行的智能算法之一,它可以对未标记的数据进行分类,因此许多专家学者将其应用在机械故障诊断中,并取得许多研究成果。FCM(Fuzzy Center Means)聚类、GK(Gustafaon-Kessel)聚类[13]和GG聚类是最常用的聚类分析法。FCM聚类和GK聚类的聚类形状几乎都类似于球体,GG聚类法则是在FCM聚类和GK聚类基础上的一种改进聚类方法,聚类形状不单一,对分布不规则数据的分类处理效果更佳[14]。
3.1 聚类的基本原理
设聚类样本集合X={x1,x2,…,xN},其中的任一元素xk(1≤k≤N)皆有d个特性指标,即xk={xk1,xk2,…,xkd},将聚类样本集合X分为c类(2≤c≤N),设其中每个分类的聚类中心向量为V=(v1,v2,…,vc)。令隶属度矩阵U=[uik]c×N,其中元素uik∈[0,1]表示第k个样本对第i类的隶属度(1≤i≤c),通过迭代调整(U,V)使目标函数Jm取得最小值:
(5)
式中m为加权指数,通常取值为2。
GG聚类算法具体步骤如下:
(1)计算聚类中心
(6)
(7)
式中Ai为第i个聚类的协方差矩阵。
(2)更新分类矩阵
(8)
若满足条件‖U(l)-U(l-1)‖≤ε则终止,否则继续令l=l+1,重复上诉步骤,直至满足条件为止。
3.2 聚类评价指标
为了验证聚类效果的优劣,本章采用分类系数(Partition Coefficent,PC)和平均模糊熵(Classification Entropy,CE)这两个指标来评价其聚类效果:
其中uik为隶属度数值,PC→1,CE→0,聚类效果越好。
4 故障诊断方法
通过上述分析,本文提出基于自适应广义形态滤波和GG聚类的轴承故障诊断法。通过自适应广义形态滤波对振动信号进行降噪处理,利用VMD法分解降噪后的振动信号,并选择包含故障特征较多的VIMF分量,求解近似熵,将所求近似熵作为特征向量输入GG聚类分析器中进行故障类型分类与识别。具体步骤如下:
(1)在固定的采样频率下采取不同类型的振动信号;
(2)利用自适应广义形态滤波器对信号进行降噪;
(3)通过VMD法分解降噪后的信号,得到若干VIMF分量信号;
(4)选取相关系数最大的2个VIMF分量信号;
(5)求取这2个VIMF信号的近似熵,构造特征向量;
(6)将特征向量输入到GG分类器,进行聚类分析,判断故障类型。
上述步骤的流程如图1所示。

图1 基于自适应广义形态滤波和GG聚类的轴承故障诊断方法的流程图
5 实验与分析
实验采用美国凯斯西储大学电气工程实验室数据[15],其中轴承型号为6205-2RS JEM SKF,负载2.237 kW,转频1730 r·min-1,采样频率为48 kHz。为模拟轴承损伤故障,分别在轴承内、外圈上和滚动体人为增加裂纹,裂纹直径为0.177 8 mm,裂纹深度为0.279 4 mm。选取轴承外圈的其中一组数据为例,所用数据的采样频率为12 kHz,采样点数为1200,随机选取4种状态下各50组样本数据。采用本文所提方法处理轴承数据,并进行分析。
5.1 实验分析
因所获取的振动信号受到不同程度噪声的干扰,利用自适应广义形态滤波对4种类型轴承信号进行滤波降噪处理,从而降低噪声的干扰,滤波结果如图2所示。
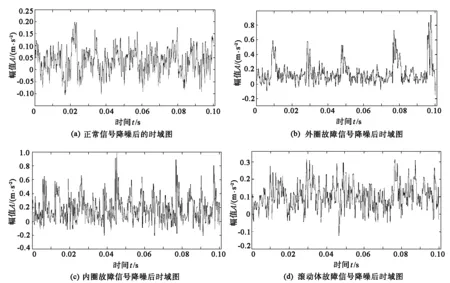
图2 4种信号自适应广义形态滤波后的时域图
对降噪后的内圈故障信号进行VMD分解,如图3所示。通过分析VIMF1和VIMF2分量与降噪后获得的信号的相关系数,发现这两个分量的相关系数之和远大于其他分量,可知VIMF1和VIMF2分量信号包含了绝大部分的故障信息。
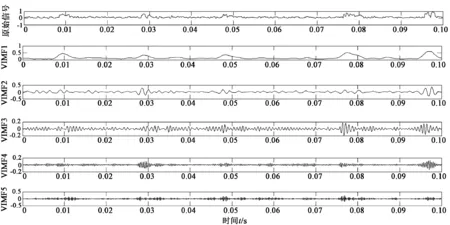
图3 降噪后内圈故障信号经VMD分解后各分量时域
选取IMF1和IMF2进行分析,每组维数为1200×2×50。对4组信号求取近似熵,得到4组2×50的近似熵,近似熵值如表1所示。
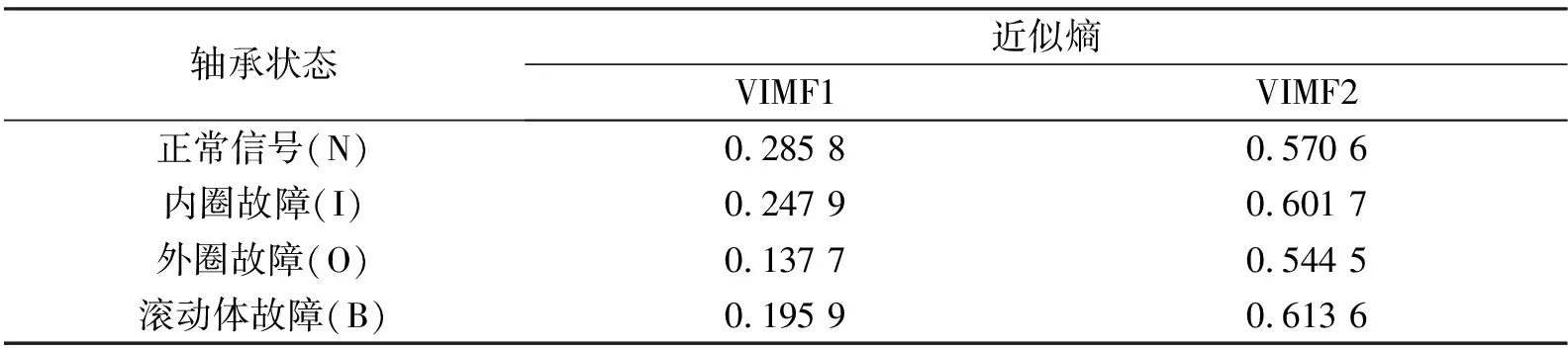
表1 前两个IMF分量信号的近似熵
由表1可知,4种不同类型轴承振动信号的IMF分量信号的近似熵值是不同的,可判断其所对应的不同类型的轴承故障的复杂度也不同。因此可以根据近似熵的不同来判断轴承故障的类型,从而达到故障分类识别的目的。将上述4组2×50的近似熵数据构成一个120×2的特征矩阵输入到GG分类器中进行聚类分析。取4个聚类中心,加权指数(m=2),迭代终止容差取值为0.000 1。图4为GG聚类分析效果图,其中空心圆圈为聚类中心。从中可得,通过GG聚类分析将轴承的4种类型的振动信号分为4个聚类中心,各数据类型紧密的聚集在聚类中心附近,但未混叠,由图可见,正常数据较分散,但故障数据距离聚类中心的间距都比较小,可以明显区分信号和故障信号。

图4 GG聚类效果图
为了识别具体故障类型,将已识别的故障类型作为标准样本,通过尚需验证的样本与标准样本之间的隶属度来判别其所属故障类型。分别用N、I、O和B表示这4种故障信号类型。随机选取4种状态的数据各3组作为待测样本进行分类识别,其中1—3组为正常信号,4—6组为外圈故障,7—9组为内圈故障,10—12组为滚动体故障,分别计算待测样本与标准样本之间的隶属度关系,结果如表2所示。从表中可以看出1—3组待测样本在N的隶属度值最大且远大于其他3组,表明1—3为正常信号,同理可得4—6为外圈故障信号,7—9为内圈故障信号,10—12为滚动体故障信号,对12组测试样本做出了准确识别,可见本文方法应用于轴承不同类型信号的分类与识别具有较好的效果。

表2 4种类型信号的诊断结果
5.2 对比实验
为验证本文方法的优越性,对聚类法和特征提取法两方面进行对比实验。
5.2.1 聚类法实验对比
为验证本文方法的可行性,分别对上述特征向量进行FCM聚类和GK聚类分析,通过计算聚类指标PC和CE值,可得FCM聚类的PC值和CE值分别为0.954 6、0.125 8,GK聚类的PC值和CE值分别为0.972 3、0.102 1,GG聚类的PC值和CE值分别为0.996 3、0.001 2。对比发现,GG聚类的PC值比FCM聚类和GK聚类的大,CE值小于FCM聚类和GK聚类。可知,GG聚类的聚类效果优于FCM聚类和GK聚类。
5.2.2 特征提取实验对比
为验证本文特征提取法的优越性,对滚动轴承4种类型信号共120组数据,分别利用EMD近似熵+GG聚类、EEMD近似熵+GG聚类方法进行聚类分析。可得,EMD近似熵+GG法的PC值和CE值分别为0.894 6、0.325 8,EEMD近似熵+GG的PC值和CE值分别为0.922 7、0.272 1,本文方法的PC值和CE值分别为0.996 3、0.001 2。对比发现,本文方法的PC值要比EMD近似熵+GG聚类和EEMD近似熵+GG聚类大且更接近1;本文方法的CE值要比EMD近似熵+GG聚类和EEMD近似熵+GG聚类小且更接近0。可得结论:本文方法的聚类效果明显优于EEMD近似熵+GG聚类方法和EMD近似熵+GG聚类方法的聚类效果。
6 结 论
本文将自适应广义形态滤波与GG聚类相结合应用于滚动轴承故障的诊断,仿真结果证明了本文方法能够准确识别出故障类型。不足之处在于自适应广义形态滤波方法,其结构元素的选取仅靠人为经验来选取,而本文对结构元素选取未作过多研究。下一步可针对结构元素及其尺寸大小选取的不同对信号滤波效果的影响展开研究。

