基于EEMD与ELM的单向阀故障诊断
张庆宇, 范玉刚
(昆明理工大学 信息工程与自动化学院, 云南 昆明 650500;云南省矿物管道输送工程技术研究中心, 云南 昆明 650500)
在矿浆管道输送过程中,往复式高压隔膜泵是其核心动力设备,单向阀是高压隔膜泵的关键部件。受工作环境和工作强度等外界因素影响,导致单向阀容易发生故障。一旦发生故障,会对矿浆管道的输送造成重大损失。
通过时频域方法对振动信号进行分析,是监测高压泵运行状态的有效方法,例如徐长航等[1]利用经验模态分解(Empirical Mode Decomposition,EMD)和Wigner-Ville分别对泵阀振动信号进行信号分解。EMD是一种经典的信号处理方法,适用于非线性、非平稳信号的分解[2]。但EMD方法存在模态混叠的问题[3],为了解决该问题,Wu等[4-5]在EMD方法的基础上,提出总体平均经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD),振动信号通过EEMD的分解有效地减少了噪声的影响。如靳行等[6]利用EEMD结合Teager能量算子(Teager Energy Operator,TEO)解决高速列车轴承早期故障中低频信号的类间分离性较弱、保持架故障难以识别的问题。陈虹屹等[7]利用EEMD奇异熵特征提取的方法减小了道岔的裂纹伤损信息的不确定性,有效提高了裂纹伤损识别率。但以上方法存在信号特征单一,难以完整表征信号特征的问题,为此本文对振动信号进行EEMD分解,得到本征模函数(Intrinsic Mode Function,IMF)分量信号,采用近似熵[8]、能量熵[9]、峭度[10]以及均方根[11]提取IMF特征,建立特征向量集,用于建立故障诊断模型,监测单向阀的运行状态。
建立故障诊断模型的本质是对故障类型进行识别。文献[12-13]摒弃了传统的多次调整神经网络输入权值和隐元偏置的策略,提出了极限学习机(Extreme Learning Machine,ELM)算法,而ELM作为一种自适应分类方法,更加适用于实际的应用,可以应用于建立单向阀故障诊断模型。结合EEMD与ELM的优点,本文提出一种基于EEMD与ELM的单向阀故障诊断方法。
1 振动信号EEMD分析
由于单向阀的工作环境复杂,其振动信号受噪声影响,消除振动信号中的噪声对特征提取具有重要的意义。EEMD方法通过加入频率均匀分布的高斯白噪声,使信号在不同尺度上具有连续性,减小模态混叠的程度。分析步骤如下:
1)在单向阀的振动信号x(t)中加入幅值均值为0.1~0.4倍x(t)的标准差的白噪声ni(t),即
xi(t)=x(t)+ni(t),
(1)
式中xi(t)为第i次加入高斯白噪声的信号;
2)对xi(t)进行EMD分解,得到k个IMF分量cj(t)和1个余项r(t)(j=1,2,…,k);
3)重复上述两步n次,并计算每次分解得到IMF分量的总体均值,以消除高斯白噪声对真实IMF分量的影响,最终得到EEMD分解后的IMF分量和余项r(t)分别为
(2)
(3)
式中cj(t)为对原始振动信号进行EEMD分解后得到的第j个IMF分量;
4)经过EEMD分解,单向阀的原始振动信号x(t)可表示为
(4)
通过以上步骤,将单向阀进行EEMD分解,得到若干个IMF分量,并提取各个分量的特征,建立表征单向阀运行状态的特征集。
2 构建振动信号特征集
在振动信号通过EEMD分解成若干个IMF分量的基础上,通过近似熵、能量熵、峭度和均方根提取故障特征,并利用计算得到特征向量构建特征向量集,用于ELM故障诊断模型的建立。
2.1 近似熵
近似熵是一种用于量化时间序列波动的规律性和不可预测性的非线性动力学参数,可反映时间序列中新信息发生的可能性。具体算法如下:
1)定义m为整数,表示原信号分解后的IMF分量长度。按顺序提取IMF分量构成的时间序列{x(1),x(2),…,x(n)}中的元素并构成m维向量X(i),
X(i)=[x(i),x(i+1),…,x(i+m-1)],i=1,2,…,n-m+1。
(5)
2)将d[X(i),X(j)]定义为X(i)与X(j)中最大差值元素的距离,即

(6)
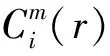
(7)
4)定义Φm(r)为x(i)的自相关度,并构建一组m+1维的向量重复上述步骤得到Φm+1(r),通过对Φm(r)和Φm+1(r)的计算得到近似熵ApEn,具体计算步骤如下:
(8)
(9)
2.2 能量熵
能量熵表示单个IMF分量在所有IMF分量能量中的能量占比,定义G(x)为能量熵,
(10)
式中P(xi)为总能量中第i个IMF分量所具有的能量占比。
2.3 峭 度
峭度是无量纲参数,其对冲击信号非常敏感,十分适用于故障诊断。定义峭度值K为
(11)
式中x为被分析的振动信号,μ为x的均值,σ为x的标准差。
2.4 均方根
对比单向阀在正常与故障的运行情况下,经过EEMD分解得到的各个IMF分量的均方根值之间存在着明显的变化,因此选用均方根值作为单向阀的故障特征指标。设xrms为均方根值,xi为某一个IMF分量,
(12)
以上4种方法可用来表征振动信号IMF分量的特征,并构建特征向量集,用于建立高压隔膜泵的故障诊断模型。
3 基于ELM的故障诊断模型
ELM是一种快速学习算法,它通过计算输入层和隐含层的链接权值,就可得到最优解[14]。并且在其训练过程中无需做出调整,只要设置隐含层的神经元个数即可,对比传统的神经网络,特别是单隐层前馈神经网络,ELM在保证学习精度下速度更快。
ELM的学习方法:给定任意N个不同的样本{(xi,ti)}∈Rn×Rm,隐层神经元数目L,激励函数选择一个连续函数G(ai,bi,xi),随机选取隐层参数ai,bi,i=1,2,…,L,ELM能以ε误差逼近任意的N个样本,表示为
(13)

按照以上方法可以建立ELM分类模型,即故障诊断模型。高压隔膜泵在运行过程当中积累大量的振动信号数据,分析振动信号,提取信号特征,建立基于振动信号特征的ELM故障诊断模型,是监测高压隔膜泵运行状态的有效方法。
4 实验分析
云南大红山管道三号高压隔膜泵站为本文实验数据来源,站中高压隔膜泵型号为TZPM系列的三缸曲轴驱动活塞式隔膜泵,运行时最高压力为24.44 MPa。现场采用型号为PCB-ICP的3组振动加速度传感器和型号为46AE的1组GRAS传声器,分别采集高压隔膜泵单向阀4组运行过程中的振动数据。采集的振动信号幅值为0.2,采样频率为42 560 Hz,采样点数为76 800点,其中噪声强度为10。
图1是故障诊断流程图。第一步采用EEMD对振动信号进行分解,由于EEMD方法是根据信号自身特征将信号自适应地分解成具有不同时间尺度的若干IMF分量,使其能很好地反映出故障信息的本质信息。如图2所示,在0~0.2 s、0.6~0.8 s和1.2~1.4 s时,图2(a)原始信号的频率较大,而图2(c)中原始信号的频率较小。在0~1.8 s时可明显看出,图2(a)、(b)中正常状态下的IMF3、IMF7、IMF8、IMF9、IMF10和IMF11分量信号的大部分频率较大,而图2(c)、(d)中故障状态下的IMF3、IMF7、IMF8、IMF9、IMF10和IMF11分量信号的大部分频率较低。由图2(a)、(b)可看出,IMF1和IMF2保留了原信号的强特征信息,IMF11和IMF12保留了原信号的弱特征信息;由图2(c)、(d)可以看出,IMF1、IMF2和IMF3保留原信号的强特征信息,IMF7和IMF8保留了原信号的弱特征信息。为了避免冗余信息对重要信息的淹没和干扰,因此省略了次要信息的图片,文中只附上了部分具有代表性的IMF分量图片。

图1 故障诊断流程

图2 EEMD信号分解
第二步利用近似熵、峭度、能量熵和均方根分别对正常和故障状态下的IMF分量提取特征。正常和故障每种工作情况下的4类特征样本总数为40个,每类特征20个,然后建立一个40×4的特征矩阵,即4维特征向量集。训练集由2×4×15个数构成,即为8×15的矩阵,其中2代表正常和故障两种运行状态,4代表特征标准的数量,15为每类特征的数量和训练集。测试集由2×4×5个数构成,即为8×5的矩阵,其中2代表正常和故障两种运行状态,4代表特征标准的数量,5为每类特征的数量和训练集。测试结果如图3所示,故障状态下的1个样本错分到正常状态下,实验测试的正确率为90%。
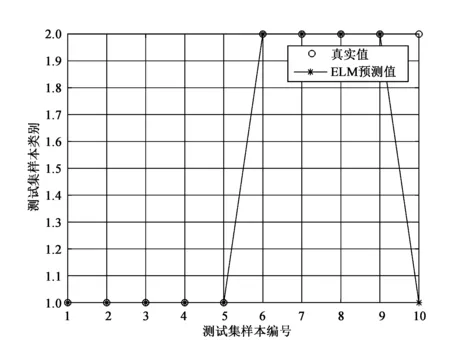
图3 ELM测试结果图
5总结
本文方法通过近似熵、能量熵、峭度和均方根对高压隔膜泵单向阀的故障信号进行特征提取,利用4种提取的特征建立特征向量集达到保留原故障信号中的故障信息,并结合ELM的优点可准确地识别高压隔膜泵单向阀的故障类型,正确率可以达到90%。总体来说,由于机械设备的振动信号在特征提取的时不易保留故障信息,因此难以准确地进行故障诊断,而本文提出的通过建立故障特征向量集并结合ELM的方法可在类似情况中有一定的使用空间。

