基于SPSS的土工击实试验数据处理

封凯强， 王家鼎*， 谷 琪， 许元珺， 王晨兴

(1.西北大学 地质学系 大陆动力学国家重点实验室， 陕西 西安 710069;2.西北综合勘察设计研究院， 陕西 西安 710003)

随着近年来西部大开发及“一带一路”倡议的实施，西北地区经济发展迅速，土地资源成为限制城市发展的主要因素之一。移山填沟已经成为山区城市开发新区的重要手段之一，山区城市包括重庆、贵阳、宜昌、十堰、延安、兰州、吕梁等地已经开展了不同规模的移山填沟工程，在创造数十亿的经济增长的同时也带来了一系列环境的改变[1]。延安自2012年4月开始进行移山填沟工程，需要对填方土体进行大规模的碾压和夯实作业，压实度是控制施工质量的重要措施。压实度为现场所测得的最大干密度与室内击实试验所测得的最大干密度之比[2]，所以如何处理实验室获得的击实数据，从而计算出更为精确的结果非常重要。

国内外研究者对于击实数据的处理做了大量研究，对于土工击实试验数据的处理有手绘法和数解法。卿启湘等[3]提出了用MATLAB实现最小二乘法进行的高次多项式插值的准则，结果发现如果残差χ2值最小及χ2分布的累积概率较小，则通过其选取的多项式阶数是比较合适的。杜瑞锋等[4]应用数值分析原理并采用分段三次多项式插值方法，自编MATLAB程序，从而更加快捷地确定击实曲线峰值点。郭亚宇[5]以残差最小为标准，通过分析几种击实试验数据处理方法的优劣，在此基础上提出了用MATLAB实现数据处理的方法。黄紫竹[6]用Origin软件对击实数据进行拟合，结果发现多项式拟合、高斯拟合、洛伦兹拟合和对数正态拟合所得的曲线均符合要求。龚新法等[7]结合Excel软件，以残差最小为标准，求得含水量与干密度的拟合多项式的解析式。戴小罡等[8]在击实试验电子表格中添加VBA程序编写的最小二乘法控件，对试验数据进行高次方的曲线拟合，求解出最优含水率和最大干密度。通过对以上文献分析可知，由于手绘法的主观性太强，绘出的曲线也比较难找到最值，精确度较低；数解法主要采用软件来拟合，常用的拟合软件有MATLAB和Excel软件。Excel拟合曲线虽然很简单，但是可以供选择的函数较少且拟合的精度较低，更重要的是无法给出模型的各个统计参数。MATLAB软件拟合曲线需要一定的编程基础，拟合过程比较复杂，不利于数据的快速处理。SPSS(Statistical Program for Social Sciences)软件是业界领先的统计分析工具，界面友好，操作简单,不需要记忆复杂的命令和过程，大多数操作可以通过菜单和对话框完成[9-10]。SPSS的曲线估计模块可以自动拟合包括线性模型、二次曲线模型及对数曲线模型在内的十几种曲线模型。曲线拟合完成后，可以直接输出各个模型的统计量。通过比较各个模型统计量的优劣，选择合适的拟合模型。

本文将SPSS软件应用于击实试验数据处理，可以快速拟合出最优的模型，从而求出更加精确的试验结果。

1 击实试验方法

本次以陕西延安某高填方场地土体为研究对象。取样所挖探井的井口为60 cm×60 cm，在探井井壁竖直方向每隔1 m切取半径为15 cm、高25 cm的圆柱状土样。试验项目包括湿密度、含水率、液限、塑限。土体的各项物理指标的测试严格按照《GB/T 50123—1999土工试验方法标准》进行，最后统计各物理力学指标，如表1所示。

表1 土体物理力学指标

击实试验时，将所取的土样进行风干，对于过于潮湿不能进行试验的土体，将其置于恒温烘箱内进行烘干，过5 mm筛，测其风干(烘干)含水率，根据土样的塑限对土体进行增湿、减湿试验，将制备好的击实试样，放置一昼夜，最后进行击实试验。击实试验所用击实仪主要部件规格如表2所示。

表2 击实仪主要部件规格表

2 击实试验数据的曲线拟合

2.1 SPSS软件拟合曲线原理

SPSS的Curve Estimayion(曲线估计)就是专门拟合曲线的，它一共提供了11种函数模型[11]。打开SPSS软件后，在数据视图中将数据导入SPSS数据框中。SPSS数据框中，每一列数据都代表一个变量。本次数据处理将含水率作为一列变量导入到数据框中，干密度作为另一列变量导入到数据框中。曲线模型的选择过程：依次打开Analyze、Regression和Cure Estimation选项，在Cure Estimation对话框，将“含水率”作为“Independent”(自变量)，“干密度”作为“Dependent”(应变量)，然后选择合适的曲线模型。如果对曲线关系不了解，可以先做散点图，预估曲线关系后，再选择曲线模型。

2.2 击实试验数据的曲线拟合

本次室内击实试验对试验所用黄土进行13、27、41击的轻型和重型试验。试验时，每种方法、每种土体的数据在20组以上。表3为一组延安某高填方场地土体重型击实试验数据，首先将击实数据导入到软件中，然后做出击实数据的散点图。根据散点图中数据的分布特征，选用二次函数和三次函数模型进行模拟，拟合结果如图1所示。

表3 重型击实试验含水率和干密度对照表

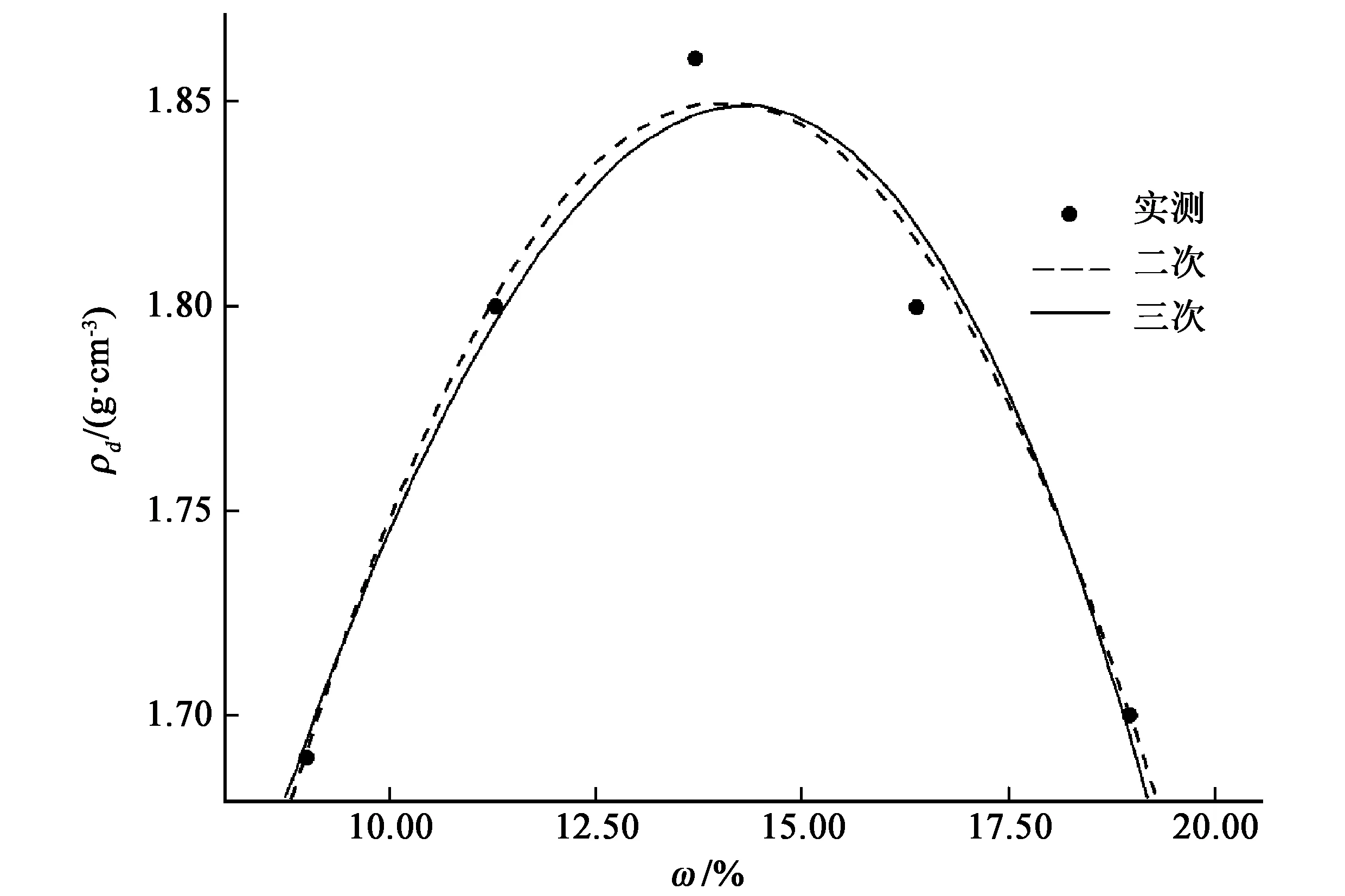
图1 三次曲线拟合

从表4中可以得到二次函数拟合系数(B)，从而可以得到拟合函数ρd=0.624 545 154 593+0.174 470 235 959×ω-0.006 217 199 123×ω2，所以最大干密度为1.849 g·cm-3，对应的含水率为14.031%(ρd为干密度，ω为含水率)。Sig为显著性分析系数，Sig<0.05时，结果就可以接受。从表4中可以看到函数的二次项、一次项和常数项显著性系数分别为0.009、0.009和0.029，均小于0.05，所以都可以接受。

表4 二次函数系数分析表

从表5可以得到三次函数拟合系数(B)，拟合函数为ρd=1.045 404 610 819+0.083 306 190 118×ω-0.000 136 042 357×ω3，所以最大干密度为1.839 g·cm-3，对应的含水率为14.287%。函数的三次项、一次项和常数项显著性分析系数Sig分别为0.008、0.009和0.004，均小于时0.05，所以拟合结果也可以接受。从显著性方面分析，二次函数和三次函数的拟合结果都是可行的，说明模型成立的统计学意义非常显著。从R2统计量看(表6)，三次曲线模型(0.991)略优于二次曲线模型(0.966)，所以三次曲线模型的拟合效果稍微优于二次模型。

表5 三次函数系数分析表

表6 模型摘要

3 击实试验结果分析

由文中2.2部分可知，三次函数模型拟合结果优于二次函数模型，所以采用三次函数模型进行拟合，进而求出各组试验结果。表7为不同工况击实试验结果，为防止出现偶然误差，每种工况选用两组试验结果。

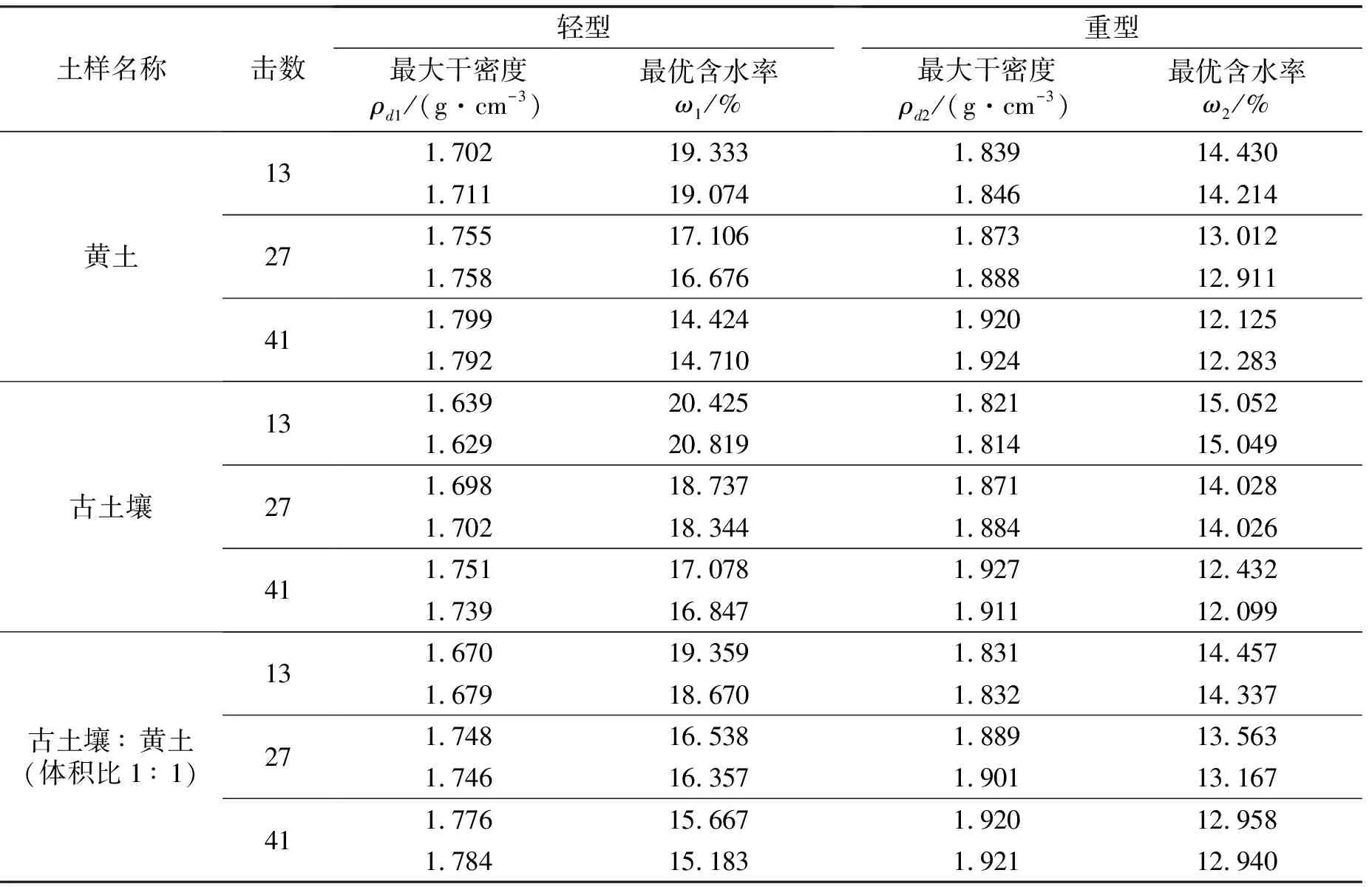
表7 不同工况击实试验结果

3.1 黄土轻型击实试验与重型击实试验的关系

依次将表7中黄土的13、27、41击轻型击实试验的最大干密度作为自变量，对应的相同击数的重型击实试验的最大干密度作为因变量导入到SPSS的数据框中(每个击数选择两组试验结果)，然后拟合它们之间关系，结果如图2(a)所示。可得到轻型与重型击实试验最大干密度之间的关系，ρd2=0.926×ρd1+0.258，拟合优度0.907(ρd1为轻型击实试验最大干密度，ρd2为重型击实试验最大干密度)。同样对黄土轻型和重型击实试验的最优含水率也进行上述操作，可以得到轻型与重型击实试验最优含水率的关系为ω2=0.463×ω1+5.410，拟合优度0.918，图2(b)为最优含水率的拟合图(ω1为轻型击实试验最优含水率，ω2为重型击实试验最优含水率)。

(a)最大干密度关系拟合图 (b)最优含水率关系拟合图图2 黄土轻型与重型击实试验结果关系拟合图

3.2 古土壤轻型击实试验与重型击实试验的关系

同样对表7中古土壤的13、27、41击轻型和重型击实试验的最大干密度数据进行拟合(拟合过程同3.1)，可以得到轻型与重型击实试验最大干密度之间的关系，ρd2=0.899×ρd1+0.352，拟合优度0.957，拟合结果为图3(a)。类似可以得到古土壤轻型与重型击实试验最优含水率的关系为ω2=3.545+0.557×ω1，拟合优度0.922，拟合结果为图3(b)。

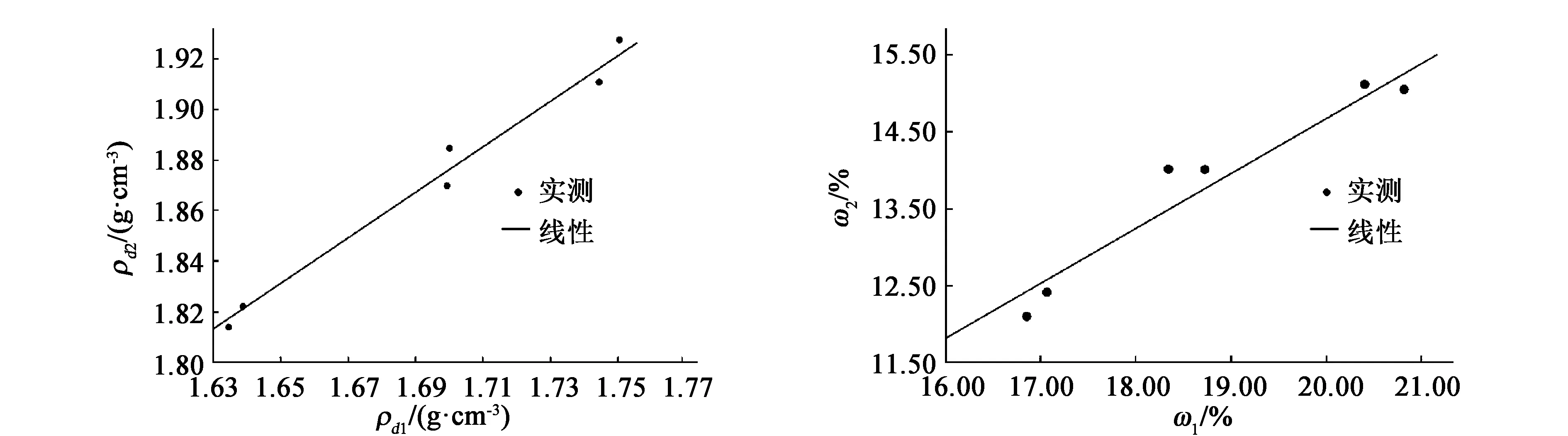
(a)最大干密度关系拟合图 (b)最优含水率关系拟合图 图3 古土壤轻型与重型击实试验结果拟合图

3.3 黄土∶古土壤(体积比1∶1)轻型击实试验与重型击实试验的关系

同样对表7中黄土∶古土壤(体积比1∶1)的13、27、41击轻型和重型击实试验的最大干密度数据进行拟合(拟合过程同3.1)，可以得到轻型与重型击实试验最大干密度之间的关系，ρd2=0.872×ρd1+0.370，拟合优度0.951，拟合结果为图4(a)。类似可以得到黄土∶古土壤(体积比1∶1)轻型与重型击实试验最优含水率的关系为ω2=6.580+0.412×ω1，拟合优度0.935，拟合结果为图4(b)。

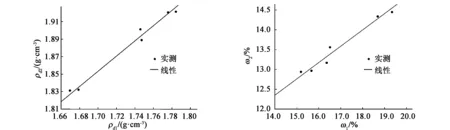
(a)最大干密度关系拟合图 (b)最优含水率关系拟合图 图4 黄土∶古土壤(体积比1∶1)轻型与重型击实试验结果拟合图

4 结 论

通过运用SPSS软件强大的数据分析和统计功能，快速准确对击实试验数据进行多项式曲线拟合，从而求出最大干密度和最优含水率。根据上述数据分析，可以得到以下结论：

(1)根据击实数据的分布特点，选用二次函数和三次函数模型拟合，结果表明二次函数和三次函数的拟合结果都是可行的，但是三次曲线模型的拟合效果稍微优于二次模型。

(2)通过SPSS对击实数据进行拟合后，求出了各种工况的试验结果，进而统计分析了黄土、古土壤及黄土与古土壤(体积比1∶1)的轻型与重型击实试验结果的关系。发现相同击数的轻型与重型击实试验的最大干密度之间呈线性关系，最优含水率之间也有类似的线性关系。并且求得了这两种击实试验结果之间的转换关系式。值得注意的是，由于不同地区土体结构及性质有所差异，该转换关系仅适用于该地区同类型土体。