偏心电极石英晶体谐振器振动特性研究

潘柏全，时俊杰，印长磊，杜红军

(空军工程大学航空机务士官学校,航空机械工程系，信阳 464000)

1 引 言

为了提高计时、通信设备的精确性和便捷性以及传感设备的准确性，设计、生产谐振频率和振动模式满足性能要求的石英晶体声波器件显得十分重要。

研究发现，石英晶体谐振器的电极材料、电极尺寸以及电极位置对其谐振频率和振动模态的影响非常重要[1-6]。由于石英压电晶体的各向异性和力电耦合特性，目前利用三维线性压电理论分析晶体谐振器的振动特性还存在很大的挑战性，想获得精确解对研究者而言是一个难题。因此，为了在石英晶体声波器件设计中获得更多有用的理论结果，通常需要简化问题从而实现近似计算，其中利用近似的二维板方程来简化问题以实现理论分析被广泛应用[7-13]。在此基础上，国内外学者一方面通过不断的实验分析来探索石英晶体谐振器和滤波器的力频特性[14-19]。另一方面在已有理论的基础上对石英晶体谐振器的振动进行理论分析，为石英晶体谐振器、滤波器等声波器件的设计和优化提供了重要的理论参考[22-25]。

但是在实际生产过程中，经常会出现电极镀层偏离板心现象。而目前对具有偏心电极的石英晶体谐振器振动特性的分析比较匮乏，只有较少的理论成果[20-21]。因此，为了提高产品设计和分析的精确性，在工业制造生产中给出精确的理论指导。本文运用Stevens和Tiersten提出的分析石英晶体平板厚度振动的二维标量微分方程(S-T方程)的变分形式，利用里兹法来研究偏心电极石英晶体谐振器的振动特性，分析不同电极偏心距、不同质量比对石英晶体谐振器振动模态的影响，同时对比不同电极偏心距情况下谐振器的谐振频率，进行误差分析，为石英晶体谐振器的生产和加工提供理论依据。

2 S-T方程及其变分形式

1986年，Stevens和Tiersten提出无电极石英晶体板和镀满电极石英晶体板的二维标量微分方程即S-T方程[13]：

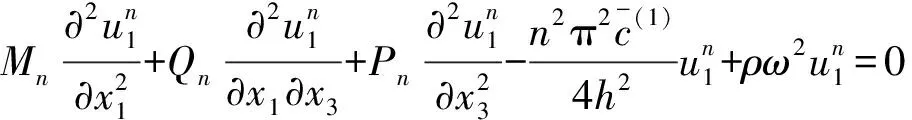
(1)

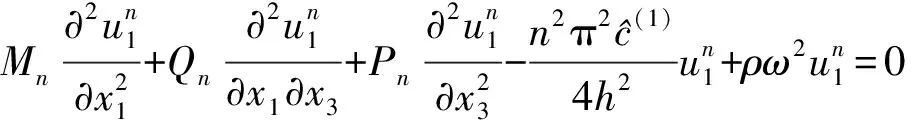
(2)

其中Mn，Pn，Qn是一些比较复杂的材料常数表达式[13]。

基于S-T方程，在文献[28]中提出利用S-T方程的变分形式来研究偏心电极石英晶体谐振器的振动特性，给出石英晶体谐振器S-T方程的变分形式[28]：

(3)

3 偏心电极石英晶体谐振器模型

本文研究对象为具有偏心电极的矩形谐振器，如图1所示。其中板长度为2l，宽度为2w，电极的长度为2a，宽度为2c，o是板的中心，o'是电极偏离板心后的中心，b是电极沿x1方向的偏心距离，d是电极沿x3方向的偏心距离。

由于电极的不对称会导致振动模态失去对称性。根据里兹法，利用文献[12]中研究的平板振动模态作为基函数，建立偏心电极石英板的厚度剪切位移场如下：

(4)

m=1,3,5…,p=0,2,4…,m1=2,4,6…,p1=0,2,4…,
m2=1,3,5…,p2=1,3,5…,m3=2,4,6…,p3=1,3,5…

其中Amp，Am1p1，Am2p2和Am3p3是未确定的常数。因为电极偏离了板心，厚度剪切振动在x1和x3方向完全失去了对称性。公式(4)的厚度剪切位移的级数展开包含基函数在x1和x3方向的对称性和非对称性，将公式(4)代入泛函公式(3)，并求得驻值条件[28]：

(5)

其中参数表达式见文献[28]，令线性方程的系数矩阵行列式为零进而得到频率方程，对于每一个频率，则对应一个振动模态。

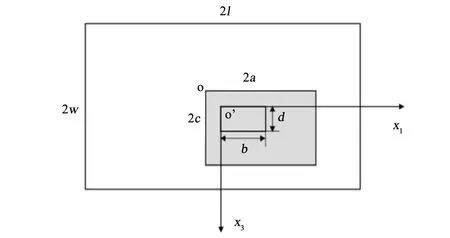
图1 偏心电极矩形石英晶体谐振器Fig.1 A rectangular quartz crystal resonator with electrode off center

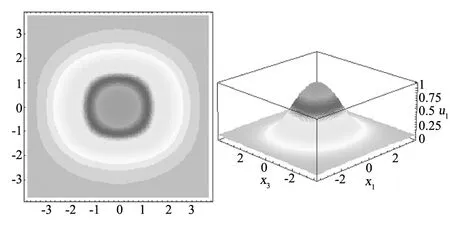
图2 对称电极石英晶体谐振器振动模态和频率 ω=6.2302000×107 1/sFig.2 Vibration mode and frequency of symmetrical electrode quartz crystal resonator ω=6.2302000×107 1/s

4 数值算例

本文研究AT切型的石英晶体平板谐振器，板厚h=0.08305 mm，此厚度下无限大无电极石英晶体谐振器的基础厚度剪切频率是10 MHz。为了便于与文献[10]对比，令a=c、l=w，取a=1.5 mm、l=3.75 mm。本文仅考虑在谐振器设计中经常用到的n=1的基础振动模态，并且为保证在数值计算中三角级数收敛较快，在x1和x3方向选取26项展开，进而得到具有8位有效数字的基础厚度剪切频率，保证谐振器设计中频率的精度。

4.1 不同电极偏心距的影响

首先考虑质量比R'为0.01时，电极对称石英晶体谐振器的振动模态。然后分别考虑电极偏离中心的三种情况：b为定值，d为变化值；然后d为定值，b为变化值；最后考虑d值和b值同时变化的情况。

图2为当d和b为零即电极无偏心情况下石英晶体谐振器的振动模态，其结果和文献[10]及文献[28]中一致，数据结果在文献[28]中得到了有限元验证，这为之后的数据对比提供参考。图中同时给出厚度振动位移的等高线视图和三维视图，模态在两个方向都是关于中心对称的，最大位移在板的中心，同时是电极中心。由于石英材料的各向异性，振动分布是椭圆形的。并且通过分析可以观察出振动主要集中在电极区域，而在趋于边缘时迅速衰减的能陷现象，能陷现象能保证在谐振器安装时可以不影响谐振器的正常工作。

通过文献[26]和[27]可知，加速度灵敏度是产品对设备产生的加速度的响应。当谐振器被安装在移动设备如导弹和卫星等高速运行的物体上时，如何降低加速度灵敏度是设计和生产谐振器的基本出发点。如图2所示谐振器的正常加速度灵敏度为零，能够在高速加速运行下保持频率的稳定性，因此当谐振器加速度灵敏度为零时是符合实际应用要求的。

图3 当b=0，d值变化的影响 (a)d=0.1a, ω=6.2302032×107 1/s;(b)d=0.2a, ω=6.2302413×107 1/s;(c)d=0.5a, ω=6.2315688×107 1/sFig.3 Effect of d (b=0) (a)d=0.1a, ω=6.2302032×107 1/s;(b)d=0.2a, ω=6.2302413×107 1/s;(c)d=0.5a, ω=6.2315688×107 1/s

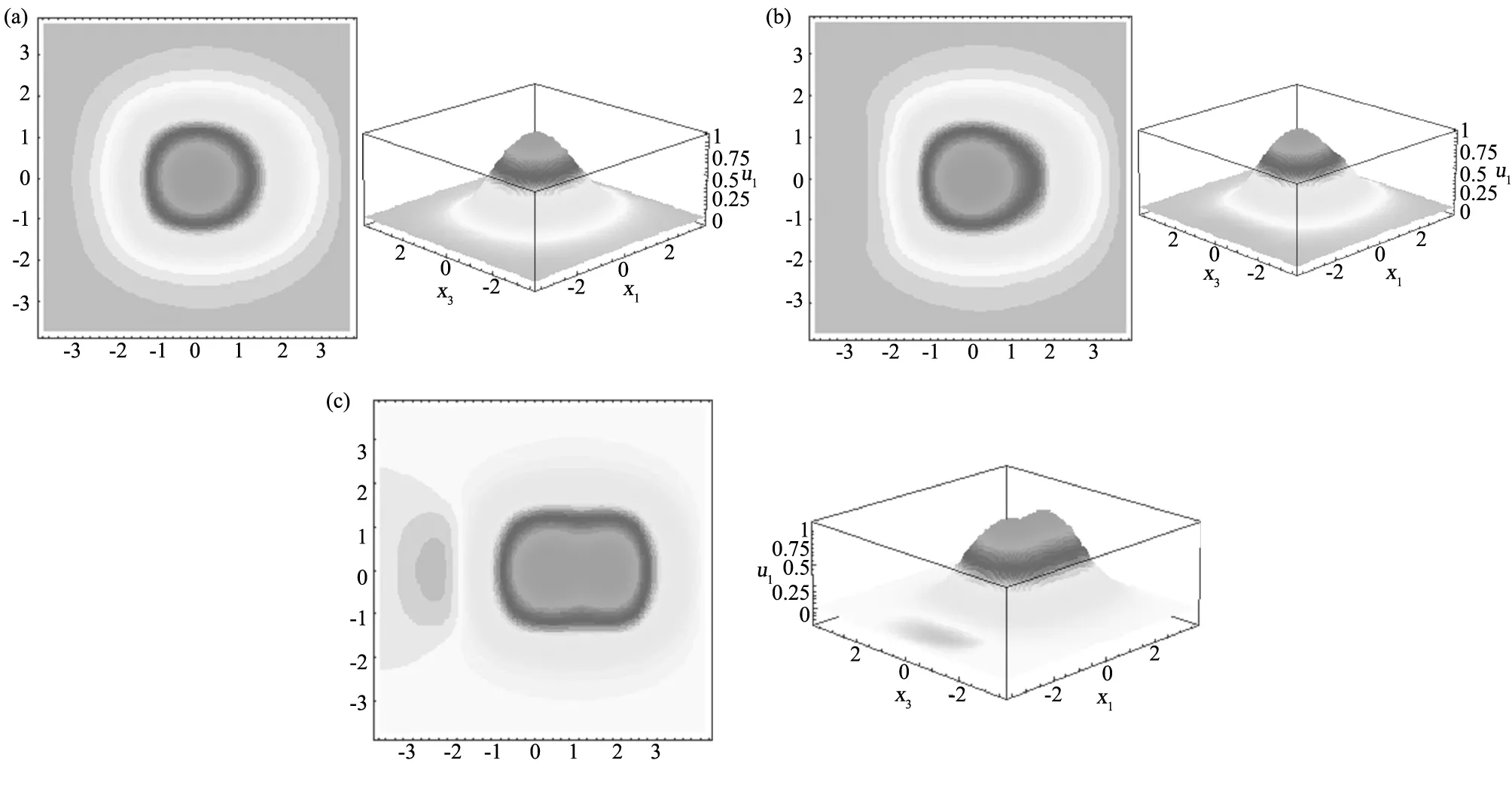
图4 当d=0，b值变化的影响 (a)b=0.1a, ω=6.2302352×107 1/s;(b)b=0.2a, ω=6.2303529×107 1/s;(c)b=0.5a, ω=6.2317250×107 1/sFig.4 Effect of b (d=0) (a)b=0.1a, ω=6.2302352×107 1/s;(b)b=0.2a, ω=6.2303529×107 1/s;(c)b=0.5a, ω=6.2317250×107 1/s

图3为仅变化d值时的振动模态和频率，研究三种不同d值下的振动模态。通过图3可以看到，当d值变化时，电极是向x3方向正向或负向移动。由于对称性，文中仅考虑电极向x3正方向的移动。如图3(a)所示，当d值变化很小时，几乎不影响振动模态。但是随着电极的移动，如图3(b)所示，可以看出模态分布逐渐偏向x3正方向，并且由于电极的偏移，板的边缘也开始出现微弱的振动。随着d值的进一步增大，如图3(c)所示，可以看出模态的偏移更加明显。同时随着d值的增大，谐振频率在增大，这是由于随着电极中心远离板的中心，可以看作电极的质量相对变小，因此导致频率增大；同时也会使板边缘的振动更加明显，这是由于石英晶体板的各项异性以及电极中心和石英板中心错位，振动叠加导致的。

图4为仅考虑b值变化时的振动模态和谐振频率。和图3中的振动行为相似，随着电极逐渐向x1正方向偏移，振动分布也逐渐趋于x1正方向，并且振动中心也随着电极的偏移发生了变化，而且在图4(c)中出现了多个振动中心，且板边缘的更加剧烈。而谐振频率随着偏离距离的增大也在逐渐增大。

图5为同时变化d和b值时的振动模态和谐振频率。通过对比发现，随着电极的移动，振动分布逐渐向板右上角移动，谐振频率也在逐渐增加。并且当电极分别向两个方向同时偏离时，对板的振动特性影响也更大。

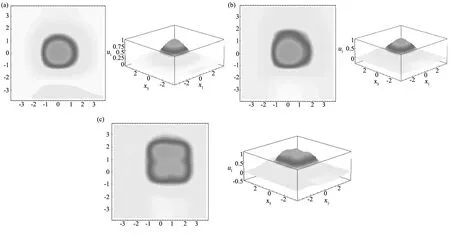
图5 b和d值同时变化的影响 (a)b=0.5a, ω=6.2317250×107 1/s;(b)d=b=0.2a, ω=6.2303696×107 1/s;(c)d=b=0.5 a, ω=6.2325955×107 1/sFig.5 Both b and d are varying (a)b=0.5a, ω=6.2317250×107 1/s;(b)d=b=0.2a, ω=6.2303696×107 1/s;(c)d=b=0.5a, ω=6.2325955×107 1/s

通过以上不同电极偏心距下谐振器的振动模态图中可以清晰看出板的振动中心随着电极的偏移发生了变化，振动模态也已经失去了对称性，这在考虑谐振器频率的稳定性时是很重要的[26-27]。尤其是对于军事车辆或武器等在运行中处于高度加速状态的设备，由于电极偏离板心造成的模态对称性的丧失会导致加速度灵敏度的增大，工作频率不稳定，从而影响设备正常运行。因此，为了保证谐振器的正常工作，谐振器的设计和制造要尽量避免电极偏离板心。

4.2 不同质量比的影响

选取石英晶体板尺寸不变，d=0，b=0.1a情况下分别取质量比R'为0.01、0.02、0.03时谐振器的振动模态，图6为不同质量比下的振动模态和谐振频率。

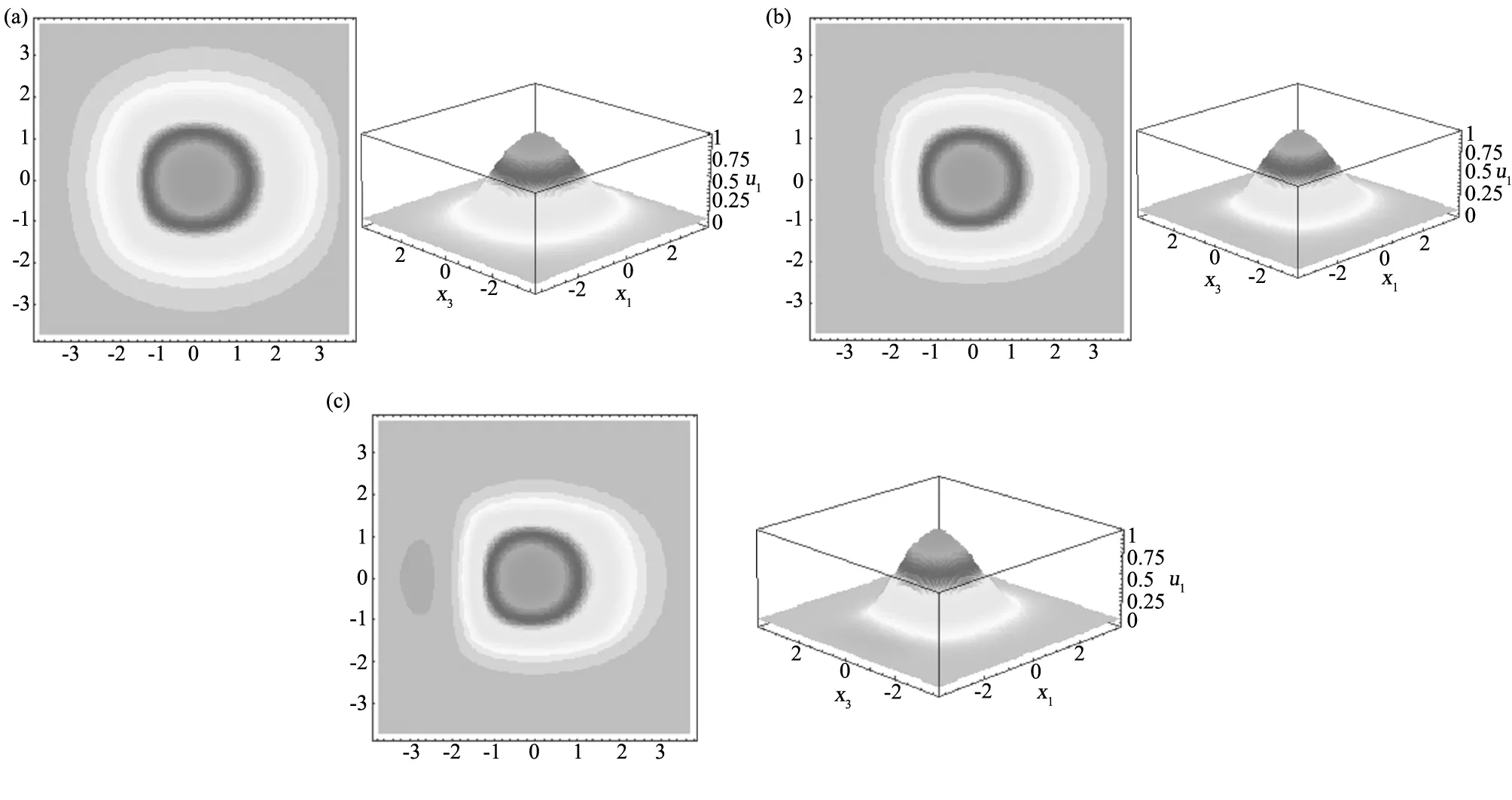
图6 d=0，b=0.1a，不同质量比的影响 (a)R'=0.01, ω=6.2302352×107 1/s;(b)R'=0.02, ω=6.1717197×107 1/s;(c)R'=0.03, ω=6.1105052×107 1/sFig.6 Effects of electrode off center on mode shape for different values of R (a)R'=0.01, ω=6.2302352×107 1/s;(b)R'=0.02, ω=6.1717197×107 1/s;(c)R'=0.03, ω=6.1105052×107 1/s

通过对比可以发现，随着质量比的增大，相当于电极的厚度增大，电极惰性对石英晶体板振动的影响也变大，使谐振频率变小导致能陷现象越来越强；同时可以看出，随着质量比的增大，板的振动分布更加集中在板的中心区域，而在趋于板的边缘时衰减的更快；并且随着电极质量比的增大，板的边缘也逐渐开始振动，这说明在谐振器的生产过程中电极质量比对谐振器的工作模态也有很大的影响。

最后，本文对不同电极偏心距离下谐振频率的误差做一个分析，表1为不同电极偏心距离下与无偏心电极谐振频率的误差分析，从对比中可以更加直观的看出偏心距离对谐振器谐振频率的影响。

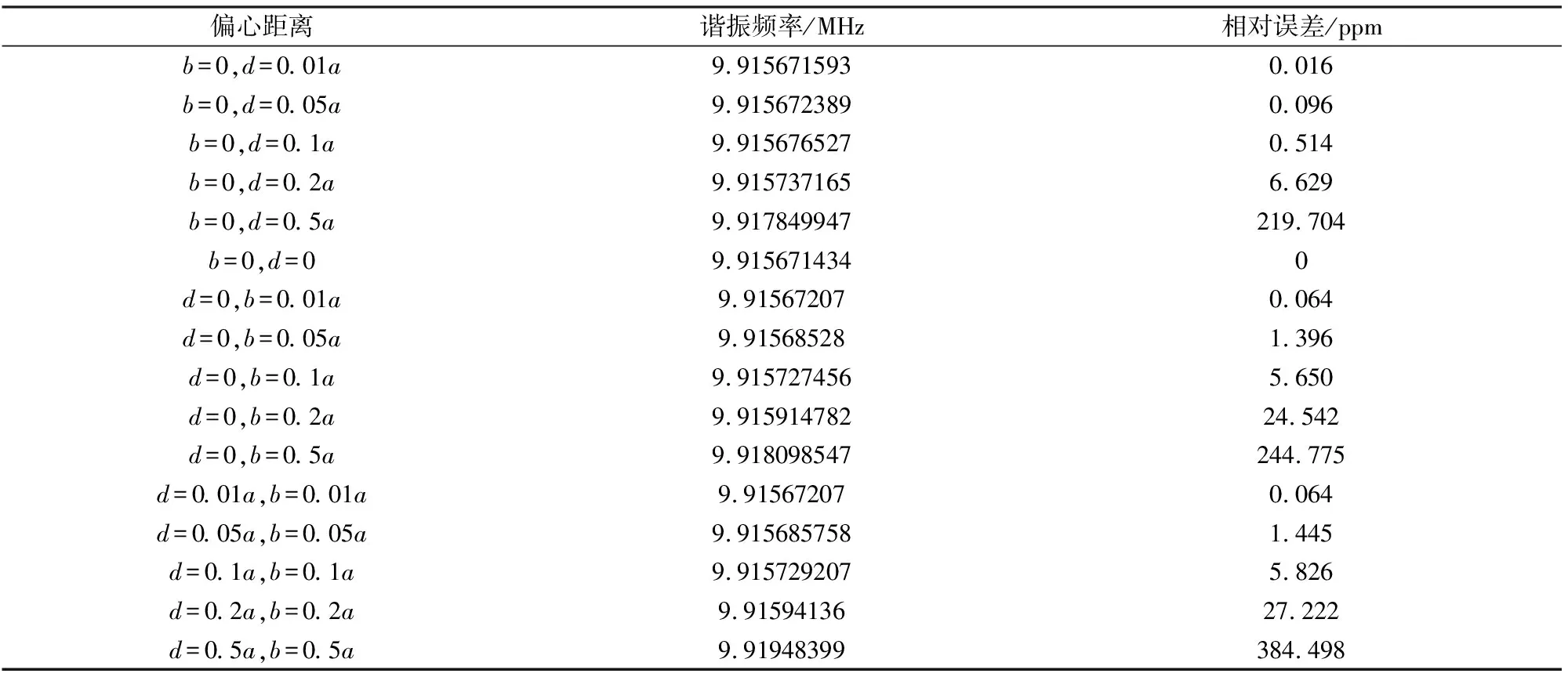
表1 不同电极偏心距离下的谐振频率误差Table 1 The resonant frequency error of different electrode eccentricity distances

通过误差分析，可以看出在b=0、d=0.01a；d=0、b=0.01a；d=b=0.01a时误差比较小，即在谐振器设计和应用中电极微小的偏移对振动模态的影响不明显，也不太重要。这和2011年夏智深等[20]研究镀有不对称电极的石英晶体平板的振动特性所得出的结论是一致的。但是当偏移值变大时，频率误差随之变大，模态不对称性也更加明显，从而会影响谐振器的设计和应用。

5 结 论

本文运用Stevens和Tiersten提出的二维标量微分方程(S-T方程)的变分形式，利用里兹法分析偏心电极石英晶体谐振器的振动特性，得出谐振器的振动模态和谐振频率。研究不同偏心距、不同质量比对振动模态的影响，发现谐振器谐振频率随着电极偏心距的增大而增大；随着质量比的增大而减小。本文主要研究生产中由于加工过程中电极偏离板心对谐振器特性的影响，为石英晶体谐振器的实际生产和设计提供了理论依据。