中欧班列去程运输组织优化模型

闫 伟，朱晓宁，邓宇君，王 力

(北京交通大学交通运输学院，北京 100044)

随着“一带一路”倡议不断推进，我国与欧洲及沿线国家的经济贸易往来频繁，物流需求旺盛。国内一些城市立足本地区位优势、路网条件和产业基础，陆续开通了直达欧洲的铁路货运班列，有力推动了我国开放型经济的快速发展。

随着中欧班列开行数量的不断提高，一些问题也逐渐显现出来。由于受各地政府地方补贴的影响，中欧班列呈现“地方主导、各自为政”的现象，造成了各平台公司之间无序竞争、政府补贴无谓加大、业务流程繁杂混乱等问题，变相增加了中欧班列的成本。针对此现状，中国铁路总公司多次召开国内协调会议。2016年4月15日，各平台公司代表在乌鲁木齐签署了《“一带一路”中欧国际货运班列联盟宣言》，选定乌鲁木齐为中欧班列西部方向集结中心，开展对全国各地中欧班列的集结编组作业，从而建立起全国各省市中欧班列运营主体的协调机制，为优化班列运输组织模式奠定基础。

国内外学者也开始对中欧班列展开研究，内容主要包括：物流通道研究、发展政策分析、运输时间缩减、运输组织模式优化等。文献[1]对目前中欧之间的货运通道进行汇总，包括海运、航空、铁路以及汽车运输通道，并对各种交通运输方式运输单位集装箱的费用和时间作比较，预测不同运输方式的货运量变化。文献[2]选择27个城市作为候选城市，综合考虑政府补贴政策和中欧班列的运营实践，利用复杂网络理论评价中国铁路、公路网各节点的重要性，利用TOPSIS模型和货物费率进行综合评估网络，最终确定10个城市作为集结中心。文献[3]对集装箱跨境运输在海运和铁路两种不同的运输方式之间的竞争问题进行研究，通过设置最佳的基础运费和时间约束建立以成本最优为目标的优化模型，实验结果表明，威慑理论在很大程度上取决于威慑目标，当威慑目标的价值较高时，两种运输方式的成本差异趋于稳定。文献[4]针对中欧班列去程班列的装车作业调度优化问题进行研究，分析装车作业的能耗构成，构建轨道门吊高能效调度优化模型，并设计遗传算法对模型进行求解。文献[5]针对中欧班列主要集结中心的装卸设备调度问题进行研究，在已知集装箱装卸位置的前提下，建立轨道门吊调度优化模型，确定最优的集装箱装卸作业顺序，使轨道门吊装卸任务完成时间最短。文献[6]在梳理中欧物流铁路通道中总结亚欧大陆桥的现状，并从通道的运作机理及发展机制对其进行研究，构建亚欧大陆桥评价体系和方法。文献[7]分析了影响班列运行速度的原因主要是口岸站能力限制、通关手续繁琐等，并提出提高班列运行速度的措施。文献[8]建立轴辐式(hub-and-spoke)运输网络的数学模型并进行数值实验，计算结果表明轴辐式运输网络更优，可以降低整个系统的运输成本。

目前，国内外学者对于中欧班列集装箱货运运输的研究，大多从中欧物流通道的成本对比及政策机制角度进行优化，探讨提高运输效率、降低运输成本的方法，较少会利用数学模型与实际数据进行定量化的分析研究。针对以上不足，本文构建网络成本优化数学模型对中欧班列去程运输组织模式进行定量分析，总结提出优化方案。

1 两种运输组织模式

1.1 直达运输组织模式

目前，中欧班列采取“点对点”的直达运输组织模式，即在国内某一城市组织同去向货源，并以该城市为始发地往欧洲某城市开行集装箱直达班列，如图1所示。

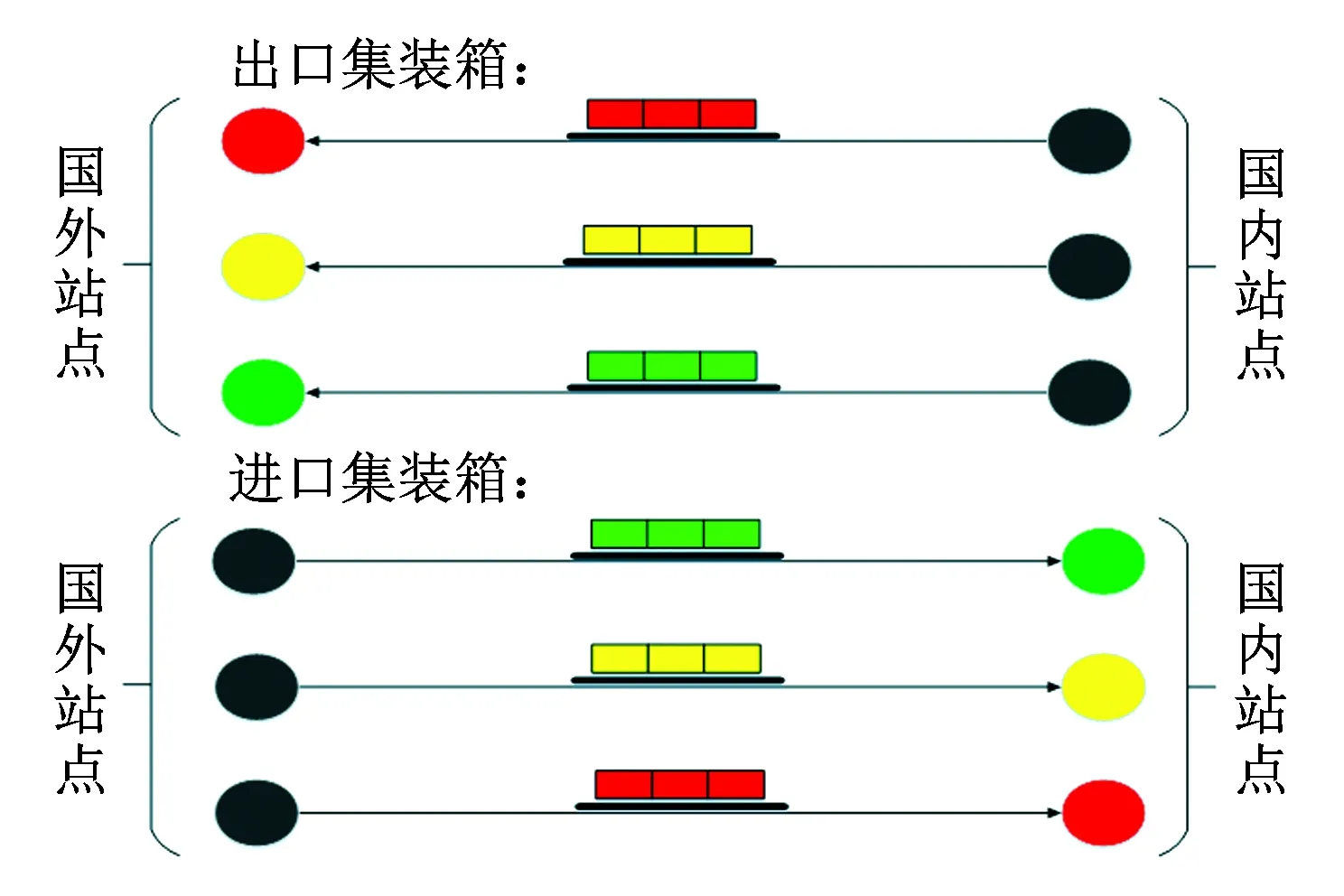
图1 中欧班列直达开行模式

在“点对点”直达开行模式下，班列就从单一始发地开行到单一终到地，由于受单一始发地与单一终到地限制，货源种类相对单一、数量相对较少，进而导致货物集结时间增加，班列开行频率一直维持在较低水平。此外，若该地区存在发往其他目的地的货物，还得先将货物转运至其他始发地，整体运输效率降低。但“点对点”直达开行模式也具有运输时间短、效率高等优势。

1.2 集结运输组织模式

中欧班列集结运输组织模式是在直达运输组织模式基础上提出的新模式，即国内各地货物将先搭载内贸班列运送至乌鲁木齐中欧班列集结中心，每批货物按照目的地进行集结，然后搭载从集结中心出发的中欧国际班列到达国外目的地。反之，欧洲运往国内各省市的货物也将先到达乌鲁木齐中欧班列回程集结中心集结，再根据每批货物的目的地搭乘不同去向的内贸班列发往各省市目的地。集结开行模式如图2所示。

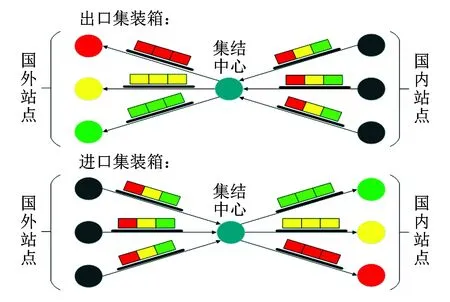
图2 中欧班列集结开行模式

集结开行模式可以提高中欧班列开行频次，降低货物集结等待时间，提高中欧班列竞争力，消除各平台公司之间的恶性竞争。但在集结开行模式下，货物在集结中心需要进行二次装卸作业，增加了额外的装卸作业成本。

2 去程运输组织模式优化模型

本文从中欧班列运营者的角度展开研究，中欧班列运营者既要考虑降低运输成本，又要考虑提高中欧班列的服务质量，而中欧班列的服务质量又主要反映在运输时间上，因此模型以降低运输成本、缩短运输时间为优化目标。本文以上述直达与集结两种开行模式为基础，构建去程班列运输组织方案的优化模型，根据该模型可以计算得出如何选用单一开行模式(直达、集结)或复合开行模式(直达+集结)作为最优去程运输组织方案。

2.1 模型假设

由于中欧班列去程运输组织方案涉及因素较多，为抓住问题本质、方便模型求解，作以下假设：

(1)本文中的集装箱中转集结次数最多一次，即集装箱可采用两种模式运输，一种为“始发地—终到地”直达运输组织模式，另一种为“始发地—集结中心—终到地”集结运输组织模式。

(2)始发地与集结中心的班列技术作业均能在集货等待时间内完成，并且模型中的班列速度为其平均旅行速度，故已考虑到了途中站点作业消耗时间。

(3)集装箱班列仅分为国内集装箱班列和中欧集装箱班列两种类型，这两种不同类型的班列除运行区段不同外，其成本参数也不相同，但同一类型班列的成本参数均相同。其中，国内集装箱班列和中欧集装箱班列也存在不同的类型(如：不同等级、速度等)，由于获取到的数据有限，故不考虑列车等级和速度等不同因素，本文仅考虑一种类型的国内集装箱班列和一种类型的中欧集装箱班列。

(4)货物时间价值与一批货物的货值呈正比例关系。

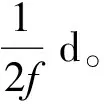
2.2 参数和变量

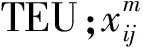
2.3 模型构建

(1)目标函数

该模型中的运输成本主要包括班列运行，口岸站换轨，集装箱作业及货物集结等待时间价值四类成本。本文以运输成本为优化目标，故目标函数中包含4个部分：①班列运行成本G1(包括固定成本和可变成本)；②集装箱作业成本G2；③货物时间价值成本G3；④口岸站换轨成本G4。模型的目标函数为

min(G1+G2+G3+G4)

( 1 )

4个部分分别为

( 2 )

( 3 )

( 4 )

( 5 )

(2)运量约束

对于任一OD(i，j)，站点i到站点j的总运量等于站点i到站点j的m条不同路径的运量之和。

∀(i，j)∈P

( 6 )

对于任一弧(i，j)，站点i到站点j线路上的总运量等于路网中流经此段线路的运量之和。

∀(i，j)∈A

( 7 )

(3)运输能力约束

对于任一弧(i，j)与任一类型集装箱班列，弧(i，j)上第t种类型集装箱班列的每周集装箱运量小于班列的开行频率与第t种类型集装箱班列的标记载重之积。

yijt≤fijt·Wt∀(i，j)∈A，∀t∈T

( 8 )

(4)站点约束

通过上面数据分析得出，当活塞环与缸套的温差超过90.9℃，存在拉缸、熔顶风险。当设备在大功率下爬坡及作业，极易导致活塞环与缸套的温差超过90.9℃，使活塞环两端口间隙消除，并被抵住而变形。首先造成拉缸，如继续工作则进一步恶化造成熔顶。

对于任一国内起始站点i，至少有一种类型的集装箱班列开行。

∀i∈S1

( 9 )

(5)班列运行路径约束

国内集装箱班列只能在国内线路段上运行(即在国内始发站至中转集结中心间开行)。中欧集装箱班列只有两种类型：一是从国内始发站开往国外的直达班列；二是从中转集结中心开往国外的班列。

fijt=0 ∀i&j∈S2，∀t∈T1

(10)

fijt=0 ∀i&j∈S1∪S3，∀t∈T2

(11)

(6)其他相关约束

zijt是0-1决策变量，当线路段(i，j)上有第t种类型集装箱班列运行时，即fijt≥1时，取1；反之，即fijv=0时，取0。

zijt≤fijt∀(i，j)∈A，∀t∈T

(12)

(13)

式中：M为一个足够大的正常量。

(7)决策变量取值范围约束

模型中所有决策变量均包含实际意义，其对应的实际变量的取值范围如下。

∀m∈Rij，∀(i，j)∈P

(14)

yijt≥0 ∀(i，j)∈A，∀t∈T

(15)

fijt∈N∀(i，j)∈A，∀t∈T

(16)

zijt∈{0，1} ∀(i，j)∈A，∀t∈T

(17)

2.4 模型求解

Lingo是一种简易的数学优化工具，可以用来求解线性和非线性的优化问题。本文中所构建的模型为混合非线性整数规划模型，可采用Lingo进行求解。

3 算例分析

3.1 算例背景

本文中考虑“三个起点、一个集结中心、一个终点、两类列车”的运输网络问题，因此，选择运量较大、发展相对成熟的渝新欧、郑新欧、汉新欧3个中欧班列进行算例分析。该问题中始发地S1包含重庆、郑州、武汉三地，终到地S2为德国汉堡，中转集结中心S3为乌鲁木齐。此外，本文中仅考虑两类班列：一类是国内集装箱班列T1，只能在国内线路段上运行(即在国内始发站至中转集结中心间开行)；另一类是中欧集装箱班列T2，其根据发站不同又可分为两种：一是从国内始发站开往国外的直达班列，二是从中转集结中心开往国外的班列。

3.2 算例数据

根据现场调研得出列车运行的数据，见表1。

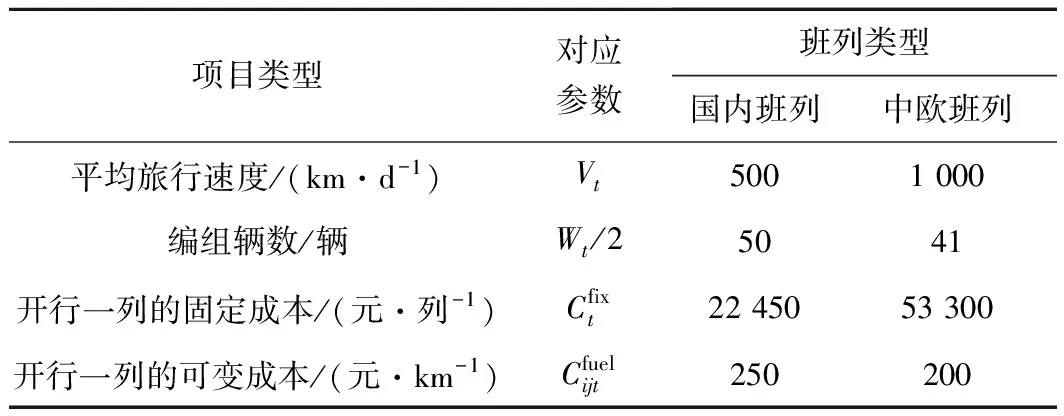
表1 列车运行相关数据

注：1.国内班列，指国内开行的集装箱班列；2.中欧班列，指开往国外的集装箱班列；3.在现场调研时未获取到具体的成本数据，只获取到了相应的运费数据，此处成本用运费作近似代替；4.一辆集装箱专用车可装载一个40英尺箱，故Wt=编组辆数×2。

根据现场调研得出站内装卸作业成本的数据，见表2。

表2 站内装卸作业成本相关数据

根据现场调研得出有关这三条班列线路的数据，见表3。

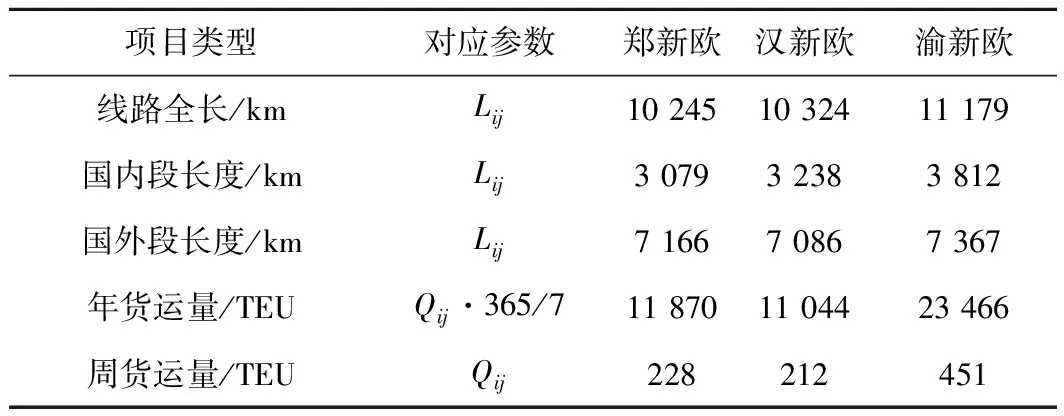
表3 三条班列线路相关数据

注：表中所列货运量数据均为2016年货运量。

本算例中全部班列只有唯一目的地j，则将国外段线路长度指定为三种班列从集拼点到目的地距离的平均数，L45=7 206 km。根据调研所得数据，目前中欧班列货源逐步向高附加值货物转移，IT产品等电子产品已经成为了大部分中欧班列的基础货源。这些电子产品的生产企业在途库存将会占用其流动资金，若该流动资金为银行的贷款资金，在货物交易成功之前，需要支付银行贷款利息。因此，本文将货物时间价值用银行贷款利息作近似代替。故单位集装箱货物的时间价值成本α约为1 350元/(TEU·d)。

3.3 算例求解

将调研所得实际数据代入模型，在处理器为Intel i5-3230M CPU@2.60 GHz、4G内存、32位Windows 7系统的笔记本电脑上，利用Lingo软件进行求解，结果见表4。

表4 Lingo求解结果

从表4可以看出，在目前的中欧班列运行条件下，铁路运输企业成本最优的开行方案为郑州、武汉、重庆，三地均各自开行直达德国的中欧班列，不采用集结开行模式，具体开行方案见表5。

具体分析上述计算结果可知，由于国内集装箱班列的平均旅行速度较低，仅为500 km/d，并且集结开行模式还需增加额外的装卸作业成本和集结等待时间。相反，中欧班列速度快，采用直达开行模式，大大缩短了在途时间，省去了集结中心的装卸作业费用。故求解得到的最优开行方案是采用直达运输组织模式。

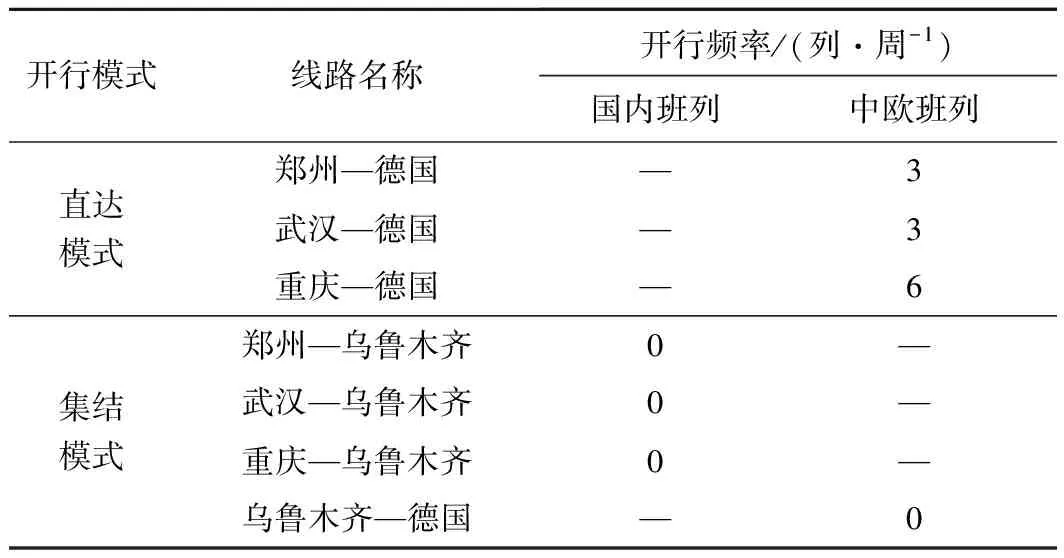
表5 列车开行方案

4 参数灵敏度分析

以上节算例为基础，在其他参数不变的条件下，分别讨论班列平均旅行速度、货物时间价值两个参数对班列运输组织模式的影响。

4.1 班列平均旅行速度对开行方案的影响

目前，中欧班列的平均旅行速度可达1 000 km/d，国内集装箱班列的平均旅行速度约为500 km/d。在此速度水平下，铁路运输企业成本最优的开行方案为郑州、武汉、重庆，三地均各自开行直达德国的中欧班列，不采用集结开行模式。国内集装箱班列的平均旅行速度仅为500 km/d，明显慢于中欧班列，并且集结开行模式还需增加额外的装卸作业成本和集结等待时间。相反，中欧班列速度快，采用直达开行模式，大大缩短了在途时间，省去了集结中心的装卸作业成本。因此，在国内集装箱班列速度慢于中欧班列速度时，最优的开行方案是采用直达运输组织模式。

下面将在保持中欧班列速度不变的情况下，分析国内集装箱班列速度变化对运输组织模式的影响。

当中欧班列保持1 000 km/d的平均旅行速度不变时，逐渐提高国内集装箱班列的平均旅行速度数值。可以发现，当国内集装箱班列速度由500 km/d增加到617 km/d时，班列的运输组织模式由直达开行模式转变为“集结+直达”复合开行模式，具体开行方案见表6。

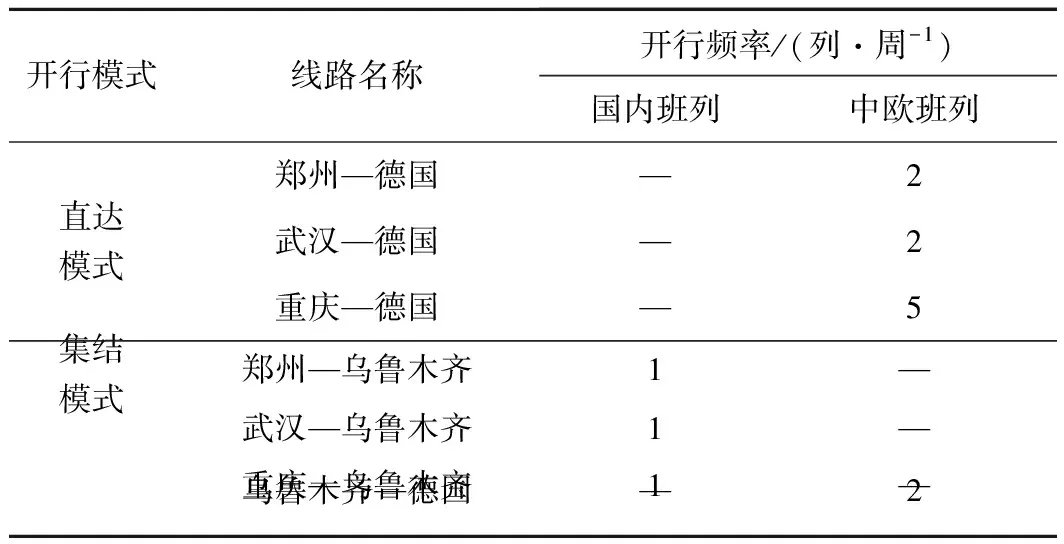
表6 列车开行方案

当国内集装箱班列速度继续增加到1 350 km/d时，运输组织模式由直达开行模式转变为集结开行模式，具体开行方案见表7。

表7 列车开行方案

在《中欧班列建设发展规划》中提到，中欧班列未来计划达到日均运行1 300 km左右的运输组织水平。当中欧班列保持1 300 km/d的平均旅行速度不变时，逐渐提高国内集装箱班列的平均旅行速度数值，发现当国内集装箱班列速度由500 km/d增加到 705 km/d时，班列的运输组织模式由直达开行模式转变为“集结+直达”复合开行模式，具体开行方案见表8。

表8 列车开行方案

当国内集装箱班列速度增加到1 999 km/d时，运输组织模式才由直达开行模式转变为集结开行模式，具体开行方案见表7。

分析以上情况可得：

(1)基于目前情况，若要纯采用集结开行的运输组织模式，开行的国内集装箱班列的平均旅行速度必须高于中欧班列的平均旅行速度，才可实现最优。

(2)在中欧班列日均运行1 000 km现有条件下：①当与中欧班列配套开行的国内集装箱班列的平均旅行速度处于500～616 km/d时，直达运输组织模式为最优方案；②当与中欧班列配套开行的国内集装箱班列的平均旅行速度处于617～1 349 km/d时，“集结+直达”复合开行模式为最优方案；③当与中欧班列配套开行的国内集装箱班列的平均旅行速度大于等于1 350 km/d时，集结中转运输组织模式为最优方案。

(3)未来当中欧班列日均运行1 300 km时：①当与中欧班列配套开行的国内集装箱班列的平均旅行速度处于500～704 km/d时，直达运输组织模式为最优方案；②当与中欧班列配套开行的国内集装箱班列的平均旅行速度处于705～1 998 km/d时，“集结+直达”复合开行模式为最优方案；③当与中欧班列配套开行的国内集装箱班列的平均旅行速度大于等于1 999 km/d时，集结中转运输组织模式为最优方案。

4.2 货物时间价值对开行方案的影响

除了列车运行速度外，货物时间价值也是一个十分重要的影响因素。目前中欧班列货源逐步向高附加值货物转移，电子产品已经成为了大部分中欧班列的基础货源。若要运送这些高附加值货物，采用何种运输组织模式最优。下面将在其他条件不变的情况下，分析货物时间价值变化对运输组织模式的影响。

基于上一节中所提到的算例，在其他条件不变的情况下，逐渐降低货物时间价值参数数值，发现当货物时间价值降低至1 310元/(TEU·d)以下时，班列的运输组织模式由直达开行模式转变为“集结+直达”复合开行模式，具体开行方案见表9。

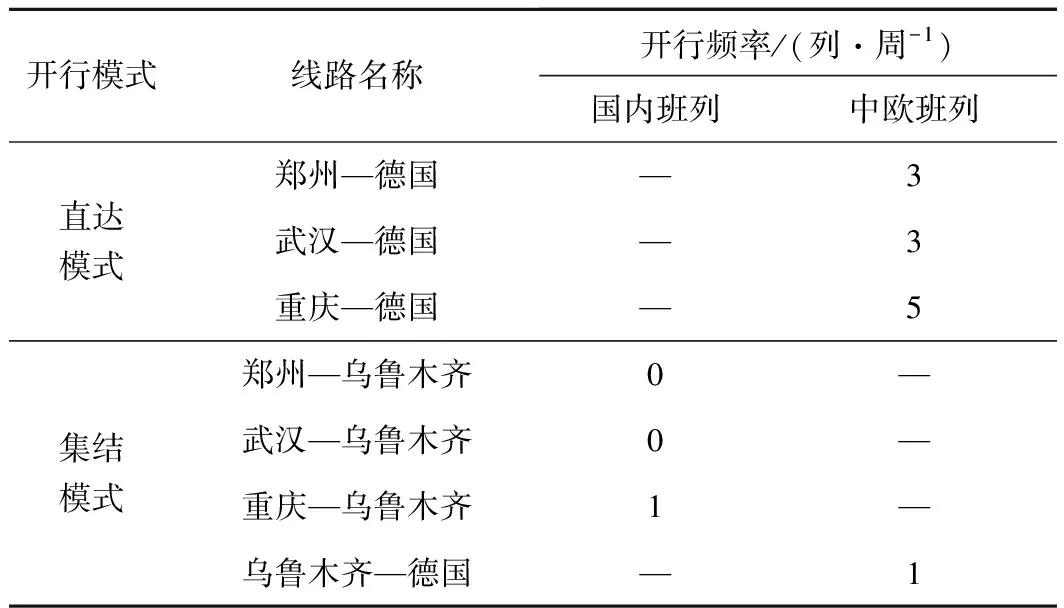
表9 列车开行方案

分析以上计算结果可得：

(1)基于目前情况，若货物时间价值大于1 310元/(TEU·d)时，必须采用直达开行的运输组织模式，才可实现最优。

(2)若货物时间价值小于等于1 310元/(TEU·d)时，采用“集结+直达”复合开行模式为最优方案。

(3)铁路部门的决策者应学会“因地制宜”，根据各地班列不同的货源结构，采用不同的班列组织模式。

5 结束语

本文根据直达与集结开行两种运输组织模式，构建了去程班列的运输组织方案的数学模型。将实际数据代入数学模型，计算得出与其相匹配的去程运输组织方案，并分析班列平均旅行速度、货物时间价值等参数对运输组织模式的影响。总结得出，基于目前情况，若只采用集结开行的运输组织模式，开行的国内集装箱班列的平均旅行速度必须高于中欧班列的平均旅行速度，才可实现最优；铁路部门的决策者应学会“因地制宜”，根据各地班列不同的货源结构，采用不同的班列组织模式。针对国内国外多起点和终点的研究将是今后的一个重要研究方向。