OMP算法对稀疏信号准确重构的一个充分条件

莫长鑫，毕 宁

(1.复旦大学 数学科学学院，上海 200433; 2.中山大学 数学学院，广东 广州 510275)

客观世界中存在着大量的所谓稀疏(或可稀疏化)信号,比如： 脑信号[1]、fMRI信号[2]等.因此，对稀疏(或可稀疏化)信号的表示长期以来都是信号分析领域研究的热点.2006年,Donoho[3],Candes等[4]引入压缩感知(Compressed Sensing, CS)概念,对稀疏信号给出了严格的数学定义,并引起数学界的广泛重视.CS作为一种新的采样理论，它能以远低于Nyquist采样频率对信号进行采样.随着科学技术的发展，数据的样本越来越庞大，如何高效地处理这些数据并从中获取关键信息以及最大限度的节约存储和传输的成本成为了一大难题.CS理论的出现为解决这个难题提供了一个好的方法并得到了不少好的结果，应用甚是广泛.

在CS中，我们经常考虑以下模型：

y=Ax+n，

(1)

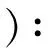
y=Ax，

(2)

此时我们称其为不带噪声的情形.式(1)的模型称为带噪声的情形.

在CS中,我们的目标之一是希望在知道观测矩阵A和观测信号y的前提下来重构稀疏信号x,那么A满足什么样的条件我们才能对稀疏信号x准确地重构呢？到目前为止,CS中用于观测矩阵的条件有零空间性质(Null Space Property, NSP)[5],相干性(Coherence)[6-8]等,而最常用的性质是由Candes等给出的受限等距性质(Restricted Isometry Property, RIP)[9-10].下面我们给出RIP的定义.

定义1[10]设A是一个m×N的矩阵,1≤k≤N是一个给定的整数.假设存在一个常数δ∈(0,1)使得

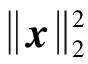
(3)

对所有k-稀疏向量x∈RN均成立，则我们称矩阵A满足k阶受限等距性质.

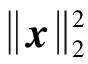
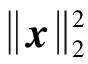
现在有很多种重构信号x的算法,比如说贪婪算法[11-13]、迭代硬阈值算法[14]、加权迭代算法[15]等,在这些算法中正交匹配追踪(Orthogonal Matching Pursuit, OMP)算法[16]是用的最广泛的贪婪算法之一.OMP算法的本质思想是选择A的列,使得在每次迭代中所选择的列与当前的冗余向量相关程度最大，然后从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度k后迭代强制停止.

首先我们给出几个重要的引理.

引理1[18]令向量u,v∈RN，并且|supp(u)|≤s以及|supp(v)|≤t.若有supp(u)∩supp(v)=Ø，则

(4)

引理2假设观测矩阵A∈Rm×N满足k-阶RIP条件并且δk<1，x∈RN的支撑集为Ω，即supp(x)=Ω，并且|Ω|=k,则我们有

(5)

以及

(6)

证 一方面，利用RIP条件及Cauchy-Schwarz不等式，我们有

(7)

另一方面，又因为

(8)

对所有的i∉Ω都成立，结合引理1，则式(6)得证.

由式(5)和(6)可以得到本文中的一个重要引理.

(9)

则我们有

(10)

证 要使得式(10)成立，则由式(5)和(6)可知，必须要有下式成立：

经过化简我们可得

根据式(9)的假设，引理得证.

在给出主要定理之前，我们先给出OMP算法的核心步骤：

输入： 观测矩阵A,向量y,稀疏度k

输出： 重构的信号x*

初始值： 残差r0=y,索引集Λ0=Ø,x0=0,t=1

Whilet≤k

步骤1 初始定义r0=y,Ω0=Ø;

步骤4 如果rt=0，则停止并输出;如果rt≠0，令t=t+1，回到步骤2,继续迭代;

end While

(11)

即

这样有Ω1⊂Ω，并且

即有

故有Ωt+1=Ωt∪{kt+1}⊂Ω.又由于

从而不难得到

即有〈rt,Aei〉=0,∀i∈Ωt.这意味着kt+1∉Ωt，即OMP算法在每一步迭代中都在Ω中选取不同的指标.综上所述，则至多k步就可将k-稀疏向量x准确重构.

文献[19]对带噪声的情形做了研究.下面我们给出文献[19]的相应结果和与本文结果相比较的一个例子，在给出例子之前我们先给出文献[19]中的相关结果.

(12)

下面我们对定理1中的结果和定理2中的结果做出比较.根据注1，我们可以知道，定理1中的RIC的条件要比定理2中的弱一些.对式(12)作出变形，我们可以得到

下面我们通过一个例子探讨M1和M2的关系.

例1对于观测矩阵A，假设其满足RIP并且RIC满足定理2中的要求(则RIC一定满足定理1中的要求)，假设向量x的稀疏度为4，即k=4，根据定理2中RIC条件可知有

若要使得M1>M2，则只需

注2由例1可知，定理1和定理2相比，不仅定理1中的RIC满足的条件要比定理2中的弱一些，而且有例子可以表明定理1中对噪声强度的要求也要比定理2中的弱一些.