试论变量的相对性及其作用
在方程、函数、不等式等数学式中出现的数量通常有常量、变量、参变量。一个数量是常量还是变量,是主变量还是参变量,其地位和性质是相对的,不是绝对的,是变化的不是静止的。
我们解决数学问题,往往需要用不同的视角,不同的思维方式,不同的数学方法对问题进行转化,将不熟悉的转化为熟悉的,繁琐的转化为简单的,抽象的转化为直观的,让看似无法解决的问题迎刃而解,从“山穷水复疑无路”到“柳暗花明又一村”。在这个转化过程中,不仅要将数学问题,在方程、不等式、函数等问题之间进行转化,同时还要对一些数量的“身份”在常量、变量、参变量之间不断地进行转化。此时把一个字母当作常量,彼时又把这个字母当作变量;此地把一个字母看作主变量,彼地又把同一个字母看作参变量。正是数学问题的转化和相应的变量在相对的变化的过程中问题就顺利得以解决。
下面,笔者举例说明变量的相对转化在数学问题转化中的必然性和作用。
例1.(1)求过圆x2+y2=R2(R>0)上一点P(a,b)的切线方程.
(2)从圆外一点P(x0,y0)引圆x2+y2=R2(R>0)的两切线,切点为A、B,求切点弦AB的方程.

图1

图2
解析:(1)如图 1 P(a,b)为切点,设 M(x,y)为切线上任一点.

这里a,b看作常量,x,y是变量,这即是过P点的切线方程.
(2)如图 2,设切点 A(x1,y1),B(x2,y2)把 x1,y1,x2,y2看作常量

分别为过A,B两点的切线方程.
∵ 两切线方程都过 P(x0,y0)点.

在等式③、④中,把 x0,y0看作常量,把 x1,x2和y1,y2看作分别处在变量x,y的位置上,那么③④两式可以看作:直线 x0x+y0y=R2过 A(x1,y1),B(x2,y2)两点.
∴切点弦AB的方程为x0x+y0y=R2.
例 2.若关于 x的方程 ax+2b=0(a>0)在区间(0,3)内有一个根.

图3

在前面的方程和函数中,把a,b看作是常量.
在不等式组和①式中把a,b看作变量。

图4
设点 A(-2,-1),P(a,b)为可行域内任一点.
问题转化为求直线AP的斜率的最大、最小值.
由图4可见,当点P在可行域内运动时,过A点的直线中,直线AO的斜率KAO最大,与直线3a+2b=0平行的直线AQ的斜率KAQ最小.
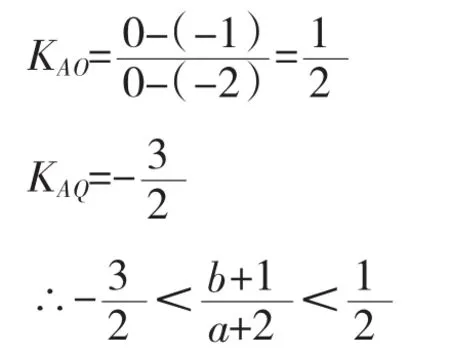
例 3.若不等式 2x-1>m(x2-1)对于 -2≤m≤2恒成立.求x的取值范围.
解析:如果将x看作主变量,m看作参变量,那么需要对m进行繁锁的分类讨论,我们换一种思维方式,把m看作主变量,x看作参变量,要2x-1>m(x2-1)对于 -2≤m≤2恒成立.
即是关于m 的一元不等式(x2-1)m-(2x-1)<0,当m∈[-2,2]时恒成立,再作一次转化,将不等式问题转化为函数问题.
就是关于 m 的一次函数 f(m)=(x2-1)m-(2x-1)当 m∈[-2,2]时 f(m)<0 恒成立.


图5
本题先对主变量和参变量的身份进行相互转换,避免了对一元二次不等式的参变量进行繁杂的讨论,然后将一元不等式的问题转化为一次函数在一个闭区间的函数值问题,问题很快得到了解决。
例 4.设函数 f(x)=x3-3x2,若过点(2,n)可作三条直线与曲线y=f(x)相切,求实数n的取值范围.
解析:f(x)=x3-3x2f′(x)=3x2-6x.
设(x0,y0)是一个切点,则过此点的切线斜率是

若将x0看作常量,则①式表示曲线y=f(x)的一条切线
因为过(2,n)点可以作曲线y=f(x)的三条切线
所以变量x0应有三个不同的值满足等式②
即方程2x3-9x2+12x+n=0有三个不同的解
改写成2x3-9x2+12x=-n
我们再把问题转化为
函数g(x)=2x3-9x2+12x与函数y=-n的图象有三个交点.为此,我们要求函数y=g(x)的极值点.
g′(x)=6x2-18x+12
=6(x-1)(x-2)
令 g′(x)=0 得 x1=1,x2=2
∵ 在(-∞,1],[2,+∞)区间内 g′(x)>0
∴g(x)为增函数
在(1,2)区间内 g′(x)<0,g(x)为减函数.
∴g(x)在x=1处取极大值g(1)=5
在x=2处取极小值g(2)=4
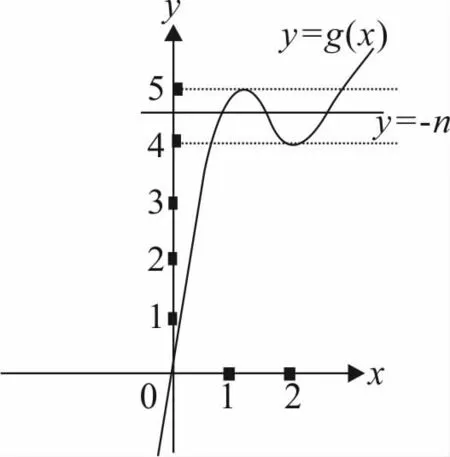
图6
如图6.若要y=g(x)与y=-n的图有三个不同的交点
则要4<-n<5
即-5<n<-4
这就是实数n的取值范围.
本题将切线问题转化为方程的解的问题,然后又将方程的解的问题转化为两函数曲线的交点问题,在这个转化过程中切点的横坐标x0在常量和变量之间转换,n也在常量和变量之间转化。
其实一个量是常量、变量还是参变量是相对的,也是统一的。变量在变化的过程中取不同的值,常量可以看成是变量在变化的过程中取同一个值。不过在观察、认识、解决问题的过程中为了叙述和处理的方便,我们需要将一些量看成常量、变量或参变量。对数学问题进行转化是为了解决问题,让一些量的身份进行转化,是为了服务于问题的转化,有利于问题的解决。所以,如果我们善于对数学问题进行转化,善于在转化的过程中让一些量(或一些字母)扮演不同的角色,那么我们分析问题解决问题的能力就会显著提高。
——卡文迪什测定万有引力常量

