遗传算法在男西裤生产流水线平衡中的应用

杨 艳，赵维强，陶惠绢，钱 惠，曹进露，赵丹萍，朱静云

(江苏阳光集团有限公司，江苏 江阴 214426)

1 引言

流水生产线是一种先进的生产组织形式，有利于机器设备和人力的充分利用。流水线不畅通，就会发生误工情况，导致生产效率降低，生产受阻。在服装生产过程中，缝纫车间流水线的平衡是其关键环节，如何合理地组织缝纫生产，解决好流水线的平衡问题，是提高服装生产效率的关键。

很多研究表明，寻找流水线平衡问题的最优解是非常困难的，最有工程意义的求解算法是放弃寻找最优解的目标，转而试图在合理的、有限的时间内寻找到一个近似于最优、有用的解。近年来这方面已经取得了不少研究成果，特别是模糊逻辑(FL)、遗传算法(GA)、神经网络(NN)、蚁群算法(ACO)、粒子群算法(PSO)等求解方法，为解决较大规模的优化问题提供了比较可行的方法，其中遗传算法在解决流水线平衡问题方面具有较好的效果。本文将遗传算法应用到男西裤生产流水线中，解决并行制造中的流水线平衡问题，以实现对流水线人员的合理安排，并对流水线的工艺进行仿真设计。

2 遗传算法

Srinivas M.等人[1]提出一种遗传算法(Adaptive General Algorithm，AGA)，能够使交叉概率Pc和变异概率Pm随群体的自适应自动改变。当种群各个体的适应度趋于一致或者趋于局部最优时，使Pc和Pm增加，以跳出局部最优；当群体适应度比较分散时，使Pc和Pm减少，以利于优良个体的生存。同时，对于适应度高于群体平均适应值的个体，选择较少的Pc和Pm值，使得该优良解得以保护；低于平均适应值的个体，选择较大的Pc和Pm值，增加新个体产生的速度。因此，遗传算法能够提供相对某个解最佳的交叉概率Pc和变异概率Pm。

与其他算法相比，遗传算法的交叉概率与变异概率不是一个固定值，而是按群体的适应度进行自适应调整。遗传算法的交叉概率Pc和变异概率Pm如式(1)、式(2)所示。

(1)

(2)

在上式中，fmax是每代群体中个体的最大适应度值；favg是每代群体的平均适应度值；f′是被选择交叉的两个个体中较大的适应度值；f是被选择变异个体的适应度值。只要设定k1、k2、k3、k4取(0，1)区间的值，就可以实现自适应调整。

从上式中可以看出，当适应度值越接近于最大适应度值时，Pc和Pm的值就越小；当等于最大适应度值时，Pc和Pm的值为零。这种调整Pc和Pm的方法对于群体处于进化后期时比较合适，因为在进化后期，群体中每个个体基本上表现出较优的性能，这时不宜对个体进行较大的变化以免破坏了个体的优良性能结构，但是这种调整方式对于处于进化初期阶段的群体效率较低，使进化走向局部最优解的可能性增加。

实行遗传算法的主要问题包括：问题的编码、适应度函数的构造、初始种群的选取、选择策略、交叉变异算子的选取、交叉变异概率的确定、算法终止条件[2]。

3 问题描述

以男西裤的缝制工艺为研究对象，它由40道大工序按照一定的顺序组成，若将其交给40名员工Pi(i=1，2，…，40)去完成，每人完成一个大工序，因这40个人的技能水平不同，他们完成不同工序所花时间也不同。因此关键在于分配这40道工序到不同的人，并使整个加工时间变到最短。

已知完成各道工序的标准时间给定，令ST(i)表示完成第i道工序100次的标准时间，ST=[41 30 25 42 30 65 28 46 57 58 86 41 37 19 28 30 29 47 64 54 33 20 34 52 47 63 44 36 65 56 38 34 55 57 65 58 36 38 68 67]。工序的生产顺序如图1所示。

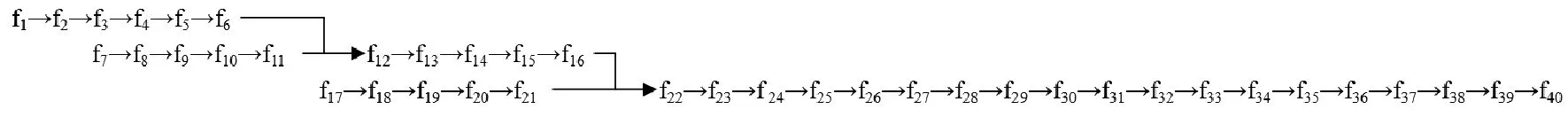
图1 男西裤的缝制工序顺序图

其中fi(i∈N，1≤i≤40)表示第i道工序；员工i完成工序j所花的时间，由式(3)确定。

Ti·j=k·STj(k∈R)

(3)

这个问题可以归为组合优化中的旅行商问题(TSP)一类，属于NP-Hard组合优化问题。解决这类问题的方法有很多，如穷举法、贪心法、动态规划方法、分枝定界法等，但是这些方法的目标函数都被定义为线性的。而本问题由于生产工艺的并行性，其目标函数是非线性的，同时随着问题规模的增加，这些精确的数学方法已无法解决此类问题。

已有研究结果表明，遗传算法对求解生产流水线问题具有较好的效果。本文将该算法应用于男西裤流水线，通过优化，自动给出比较合适的交叉概率和变异概率，从而显著提高搜索效率。

4 基于遗传算法的男西裤流水线分析

4.1 编码

本文选用一种基于顺序表达的实数编码方式。染色体的长度等于缝制工序数，全部员工的上岗顺序编码为一组自然数编码的字符串，即染色体；染色体的基因取1～40之间的自然数，分别代表员工1～员工40。例如1，2，3，4……40。

4.2 适应度函数

适配值函数为：

其f(m)表示完成40道工序实际所用去的时间。

f1=T1+T2+T3+T4+T7+T8+T9+T10+T11+T12+T40

f2=T5+T6+T7+T8+T9+T10+T30

f3=T11+T12+T13+T16+T17+T20+T29+T30+T31+T32+T33+T34+T35+T36+T37+T38+T39+T40

f4=T14+T15+T16+T17+T20+T29+T30+T31+T32+T33+T34+T40

f5=T18+T19+T20+T29+T30+T31+T32+T33+T40

f6=T20+T28+T29+T34+T35+T36+T37+T40

f7=T21+T22+T23+T26+T27+T30+T31+T32+T33+T34+T35+T40

f8=T24+T25+T26+T27+T3

4.3 初始种群的选取

初始化种群：初始化种群是将优化问题的一组初始可行解，即全部员工的上岗顺序编码为一组自然数编码的字符串，即染色体；染色体的基因取1～40之间的自然数，分别代表员工1～员工40。初始种群中的染色体随机产生。

把上一步生产的染色体种群按照评价函数进行排序，采用传统的轮盘赌的方式选择产生父代染色体。个体被选中的概率与其在群体中的相对适应度成反比。

4.4 复制算子

从群体中选择优胜个体淘汰劣质个体的操作为选择算子。本文采用精英原则的轮盘赌选择机制，即经交叉后的子代需与父代进行比较，只有当子代的适应值大于父代的适应值时，才用子代代替父代，否则保留父代。

4.5 交叉 变异算子的选取

在男西裤流水线的平衡问题中，由于染色体上每位基因表述的是完成该工序的员工号，所以交叉、变异的概率大小更直接地体现为参与交叉、变异的基因位数的多少。参与交叉、变异的基因位数多，则该工序的操作员工顺序改变大；参与交叉、变异的基因位数少，则该工序的操作员工顺序改变不明显。所以如果不考虑参与交叉、变异的基因位数，则所谓的交叉、变异概率显得毫无意义。因此，把交叉、变异概率理解为参与交叉、变异基因位数的多少。

交叉长度=PC×NUM，变异长度=Pm×NUM

其中PC：交叉概率，Pm：变异概率，NUM：染色体长度。

交叉算子：将获得的父代按适应度值进行排序，让前半部分与后半部分分别进行交叉，在两个交叉的双亲中任意选取一个交叉位置，交叉长度= PC×NUM，再确定另一个交叉位置，由此确定交叉的基因段[3]。其后代在这段基因里的编码按照另一双亲的顺序排列，其余编码的排列顺序不变。因为双亲都是可行解，则通过这样的方法产生的后代也必然是可解行。变异算子：为了加快算法的收效效果，在父代上任意选取一个变异位置，变异长度=Pm×NUM，再确定另一个变异位置，由此确定变异的基因段，在变异的基因段，进行随机排序，得到新的染色体。

4.6 改进的自适应交叉 变异概率的确定

在遗传算法中，个体的适应度值越接近最大适应度值，交叉概率与变异概率就越小；当等于最大适应度值时，交叉概率与变异概率为零[4，5]。这种调整方法在群体处于进化后期时是比较合适的，但在进化初期对进化是不利的，因为在进化初期群体中的较优个体几乎处于一种不发生变化的状态，而此时的优良个体不一定是优化的全局最优解，这增加了进化走向局部最优的可能性。

遗传算法是将交叉概率PC和变异概率Pm分别改为式(4)、式(5)，使群体中最大适应度值的个体的交叉概率和变异概率不为零，分别提高到Pc2和Pm2。

Pc=

(4)

Pm=

(5)

当f′=fmax时，Pc=Pc2>0；当f=fmax时，Pm=Pm2>0。为了保证每一代的最优个体不被破坏，同时采用最优保存策略，将其直接复制到下一代中。上式中，取Pc1=0.95，Pc2=0.6，Pm1=0.15，Pm2=0.001。

4.7 终止条件

令fmax[k]为第k代种群中最优个体的适应度值，favg[k]为第k代种群中所有个体适应度值的平均值。分别定义第k(k≥10)代之前的前10代的种群最优适应度值的平均值和第k(k≥10)代之前的前10代的个体适应度值的平均值。

(6)

(7)

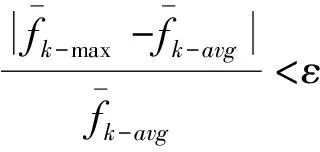
5 实验与结果分析

5.1 实验

为了验证上述算法的有效性，用Minitab实现上述算法。在实际生产中，员工的熟练程度接近于标准时间的比较多，本文取：

(8)

其中x是均匀分布与[0，10]之间随机数。通过上式设定的k使员工的实际操作时间处于标准时间的0.5倍～1.5倍的概率为70%，使员工的实际操作时间处于标准时间的0～0.5倍的概率为10%，使员工的实际操作时间大于标准时间的1.5倍的概率为20%。

5.2 结果分析

这里随机选取员工完成各道工序的时间值，其中适应度最高的个体如表1所示。

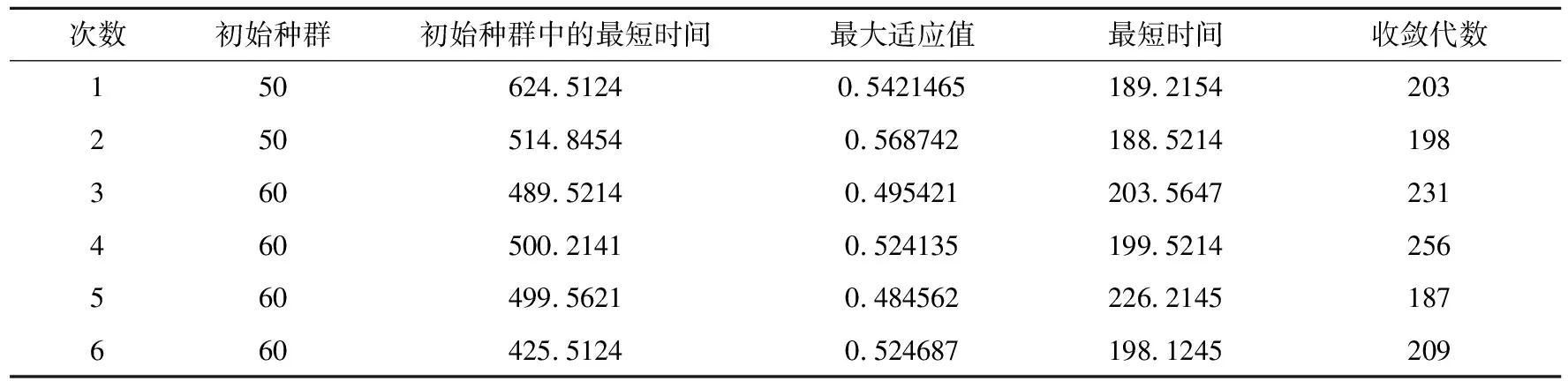
表1 遗传算法分析表

运用遗传算法，得到的最好结果为19-38-15-11-37-30-33-13-6-39-14-23-35-20-5-3-34-21-29-32-22-1-31-26-16-27-36-2-40-24-10-17-25-9-4-8-18-28-12-7，与现有的手工分配相比，时间缩短的很多。

6 结语

文本利用遗传算法解决了男西裤缝制流水线的平衡问题，不需过多的数学计算，且能够在搜索过程中自动给定交叉概率和变异概率，显著提高了收敛速度，且相对于其他方法而言，更容易得到最优解，具有简便高效的特点。