半球谐振陀螺全角模式信号处理控制方法

张岚昕，赵万良，李绍良，成宇翔，王 伟

(1.上海航天控制技术研究所，上海 201109；2.上海惯性工程技术研究中心，上海 201109)

0 引言

半球谐振陀螺具有结构简单、可靠性高、寿命长、精度高且无累积误差等特点，在空间探测、航空航海、精密设备等领域发挥着越来越重要的作用。半球谐振陀螺与其他类型的固体波动陀螺的工作原理类似，当谐振子在外加特殊频率的激励作用下会产生四波腹的谐振振型，陀螺随载体在惯性空间中绕敏感轴转动时，四波腹振型在科里奥利力的作用下会发生实时进动。通过外部电路将陀螺谐振子振动信号转换为电信号，并通过信号处理的方法从电信号中得到谐振振型的进动特性，就可以获取载体的角度或角速度信息。半球谐振子的结构图以及四波腹振动示意图如图1所示。

(a)

(b)图1 (a)半球谐振子结构图，(b)四波腹振型示意图Fig.1 (a)Structure of hemispherical resonator; (b) Transformation of four-wave vibrating pattern

按照工作原理，半球谐振陀螺可以分为力平衡(Force-to-Rebalanced)工作模式和全角(Whole-Angle)工作模式。较之于力平衡工作模式，全角模式半球谐振陀螺具有较大的动态范围和响应速度，同时其信号处理和振型控制算法也更为复杂。全角模式的工作原理为，当有角速度输入时，谐振子受到沿着与角速度和振动方向均垂直的方向产生的科里奥利力为：

F=2mΩ×v=-2mΩAωsin(ωt)

(1)

在科里奥利力的作用下，谐振子振型转动角度与载体的转动角度会相差一个滞后角度θ，称θ为进动角或滞后角(见图2)，进动角与载体转动角度θreal存在固定的比例关系如下：

θreal=kθ

(2)

其中，比例系数k称为进动因子，k的大小仅与陀螺谐振子的材料和结构有关，当陀螺表头的物理状态确定时，k可以被视为常数。因此，在全角工作模式下，一般通过外部电路在陀螺表头输出的振动信号的基础上进行一系列的处理和解算，最终得到谐振振型的进动角，并用它来表征陀螺所在载体的实时转动角度。

(a)陀螺未发生进动的状态

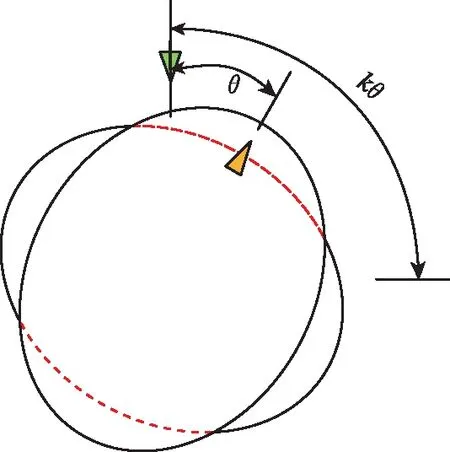
(b)陀螺所在载体发生转动时谐振振型发生进动图2 振型进动状态下示意图Fig.2 Vibrating pattern under real-time precession

进动角度的解算精度与陀螺谐振振型的稳定性有很大关系，振动振型的频率、波腹点幅度、波节点幅度的不稳定均会导致进度角的解算误差。因此，为了保证全角模式下半球谐振陀螺的敏感精度，陀螺外部信号处理电路须包含波腹点幅度检测与控制、波节点幅度检测与控制、频率跟踪回路和角度信号解算等几个部分。其中频率跟踪和波节点控制的效果对角度敏感的精度影响较大，频率跟踪回路的参数不合理时，会导致解调载波的相位与陀螺谐振相位差不收敛至0°，而是收敛至90°或-90°，并最终导致驱动力的相位混乱，振动状态发散；而当波节点的幅度未被抑制到0且存在波动时，会造成幅度检测量的波动和解调载波相位的波动，并最终影响角度敏感的精度。

本文介绍了一种半球谐振陀螺全角模式的控制方法，并分析了该方法的误差来源和误差抑制的方法。

1 半球谐振陀螺动力学模型

半球谐振陀螺的谐振子四波腹振型的振动参数耦合了振动幅度、振动频率和进动角度等信息。全角模式下半球谐振陀螺通过陀螺敏感电极将陀螺的物理振动信号转换为电信号；并通过信号处理算法将振动幅度、振动频率和进动角度等信息分离和解算出来；并通过控制算法稳定谐振子的谐振振型，保证陀螺的进动角度稳定收敛。

当半球谐振陀螺谐振子振动的物理模型被简化为弹簧质量阻尼系统时，其二阶动力学模型如式(3)[1-2]：

(3)

其中，Ω为载体平台转动速度，k为谐振子进动因子，k′为向心力增益系数，ω为陀螺谐振子固有振动频率，x和y为2个相互正交的信号轴向上的振动信号，fx和fy为从x和y两方向上施加的控制作用，在半球谐振陀螺中，x和y的几何放置位置相差45°。

在式(1)的基础上，通过平均法可以得到陀螺谐振子在x和y位置上的振动位移表达式如下[3-4]:

x=acos(ωt)cos(θ)-qsin(ωt)sin(θ)

y=acos(ωt)sin(θ)+qsin(ωt)cos(θ)

(4)

其中，a和q为谐振振型的长轴和短轴，θ为进动角，x和y为陀螺通过相隔45°的2个电极读出的信号，这2个电极的信号的物理意义是陀螺振动信号向2个电极方向的正交变换，如图3所示。

图3 谐振振型正交分解示意图Fig.3 Orthogonal decomposition of vibrating pattern

2 半球谐振陀螺信号处理与控制

全角模式半球谐振陀螺信号处理与控制的目的是维持实时进动过程中的振型稳定并解算出实时进动角度，其主要包括以下4个部分：维持谐振能量不发生衰减的波腹点控制回路；抑制波节点幅度进而抑制陀螺敏感误差的波节点控制回路；实时跟踪陀螺谐振频率和相位，产生解调参考信号的锁相环回路；进动角度动态检测部分。陀螺信号处理与控制的结构框图如图4所示。

图4 全角模式半球谐振陀螺控制框图Fig.4 Control scheme of whole angle mode HRG

电极读出的陀螺信号如式(4)，相对于检测电极输出的陀螺谐振信号而言，半球谐振陀螺谐振振型的长轴振幅a、短轴振幅q以及陀螺动态进动角度θ等振动状态量均为低频慢变信号，需要通过信号处理的方法将他们从陀螺高频的谐振信号中提取出来。

可以通过锁相环得到与实时谐振振动信号同频同相的解调参考信号Vc与Vs，该信号与真实谐振信号有相位差φ。

Vc=cos (ωt+φ)
Vs=sin (ωt+φ)

(5)

使用参考信号通过乘法解调的方法将陀螺信号的频谱特征向低频和二倍频方向进行频谱搬移，并经低通滤波将包含振动状态量的低频慢变信号Cx、Cy、Sx、Sy提取出来。

(6)

对低频慢变信号进行组合运算，可以得到陀螺谐振振动状态量,如式(7)：

E=Cx2+Cy2+Sx2+Sy2=KE(a2+q2)
Q=2(CxSy-CySx)=KQ(aq)
S=2(CxCy-SySx)=Kθ(a2-q2)cos(2θ)
R=Cx2-Cy2+Sx2-Sy2=Kθ(a2-q2)sin (2θ)
L=2(CxSx+CySy)=KL(a2-q2)sin(2φ)

(7)

其中，E既表征了谐振振型的能量，当波节点幅度q被抑制到0时，E又反映了长轴的振幅；Q表征了波节点振动的幅度。E信号、Q信号分别作为波腹点和波节点控制回路的检测信号，经PI控制器分别得到波腹点控制信号Fa和波节点控制信号Fq。控制作用Fa与Fq需要利用x和y方向的驱动电极施加到谐振子上，因此，需要将Fa与Fq分别分解到x和y方向上，同时还需要将该控制信号与陀螺谐振频率进行调制，得到驱动作用Fx和Fy。

Fx=Facos(θ)cos(ωt-90°)-
Fqsin (θ)sin(ωt-90°)
Fy=Fasin(θ)cos(ωt-90°)+
Fqcos (θ)sin(ωt-90°)

(8)

S和R信号做比值可以得到进动角度的正切函数tan(2φ)，由于比值消元的效果，波腹点和波节点的振幅不稳定性不会影响进动角度的计算结果。

L表征了锁相环产生的解调参考信号与谐振信号的相位差。L信号作为锁相环鉴相器的输出，通过改变振荡器参数使L逐渐收敛，产生与谐振信号同频同相的解调参考信号。要注意的是，由于L=KL(a2-q2)sin(2φ)，在2φ较大时有可能会收敛于2φ=180°。因此，在锁相环参数匹配不佳时，可能会导致解调参考信号相位翻转，并最终引起控制结果发散。

3 建模仿真分析

根据谐振子动力学分析和全角模式半球谐振陀螺谐振信号处理与控制算法，搭建了Simulink仿真模型。其中仿真的陀螺谐振频率ω=5000Hz，进动因数k=0.3。分别针对波腹点控制、波节点控制、频率跟踪以及角度解算等几个部分进行仿真分析。

3.1 波腹点控制

波腹点的稳定性和精度会影响频率跟踪的精度进而对陀螺精度产生影响，仿真采用阶跃信号作为波腹点的激励信号。由仿真结果可知，在PI控制参数调整合理的状态下，波腹点信号响应时间约为0.15s，稳态误差小于0.02V，如图5所示。

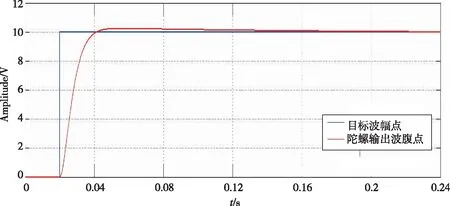
图5 波腹点阶跃信号输入下的控制仿真图 Fig.5 Simulation of energy control under the antinode step input

3.2 波节点控制

波节点的稳定程度可以影响波腹点与频率跟踪的控制效果，根据算法波节点应被抑制到0V附近。通过实时数值仿真可知，当不施加波节点控制时，波节点的存在会导致谐振振型的相位漂移，引起x和y信号之间产生相位偏移，x和y信号的李萨茹图为椭圆型，仿真结果如图6所示。

当施加波节点控制后，x和y信号之间产生的相位偏移被消除，相位差为0°或180°，李萨茹图为一条直线，由仿真结果可知，波节点控制响应时间小于0.02s，稳态误差小于1×10-7V，仿真效果如图7所示。

(a) (b)图6 (a)图为在波节点未被抑制到0时振动信号，x与y之间存在一个相位差；(b)图为在波节点未被抑制到0时，x和y信号的李萨茹图Fig.6 (a) shows signal x and y when quadrature signal is not 0; (b) shows Lissajous-graph of signal x and y

(a)

(b)图7 (a)为波节点信号被抑制为0时的振动信号与李萨茹图，相位差随波节点一起收敛于0；(b)为波节点控制仿真结果图，上图为波节点输出，下图为波节点控制误差Fig.7(a) shows signal x and y and their Lissajous-graph when quadrature signal approaches to 0; (b) shows error of quadrature control loop

3.3 频率跟踪

通过锁相环进行频率跟踪的输出信号被用于乘法解调和驱动调制的参考信号，其与陀螺半球谐振子实时振动信号的相位差会影响波腹点信号解调、波节点信号解调以及角度解算的精度。数值仿真结果显示(见图8)，频率跟踪稳定工作的情况下，相位误差小于0.5×10-7。

图8 频率跟踪仿真结果图(上图红线为陀螺实时谐振信号，蓝线为跟踪振动信号；下图为实时频率跟踪误差)Fig.8 Simulation of frequency tracking result(In the first graph, the red thread represents vibrating signal of gyro, the blue thread represents frequency track’s output. The second graph shows error of frequency control loop)

3.4 角度跟踪

角度敏感是全角模式下半球谐振陀螺的最终目的，并且角度敏感的精度也直接影响了驱动作用的施加效果。将30°角度阶跃信号和10(°)/s斜坡速率输入作为激励输入对角度解算进行仿真分析，仿真结果显示，经角度解算的动态响应时间小于0.05s，稳态误差小于0.05°，如图9所示。

(a)30°阶跃角度输入

(b)10(°)/s速率斜坡输入图9 角度解算仿真结果图Fig.9 Results of simulation for angle solution

4 结论

全角模式下半球谐振陀螺的性能指标受谐振波形的稳定性和频率跟踪精度的影响，本文针对半球谐振陀螺全角工作模式的动力学过程进行了分析和建模，并介绍了一种全角模式下半球谐振陀螺控制和信号处理方法。该方法通过离散电极取得相互正交的谐振子振动信号x和y；通过乘法解调与低频信号组合运算，实现了波腹点、波节点、谐振频率和进动角度的实时检测；通过波腹点控制、波节点控制、频率跟踪等3个回路，实现了谐振子四波腹振型状态的稳定。最后针对数值仿真模型的仿真结果加以分析，验证了此方法的可行性。