基于滑模变结构和扩张状态观测器的电动舵机复合控制方法
吴 真,曹东海,熊官送
(北京自动化控制设备研究所,北京 100074)
0 引言
舵机是飞行器控制系统的重要组成部分,是控制系统中特性复杂、能耗高、配套数量多、工作环境恶劣的子系统,其性能和可靠性对姿态控制具有决定性的影响,直接决定了飞行器飞行结果的成败和精度。在实际飞行过程中,舵偏角的变化和环境中风阻等因素的影响导致舵机承受的铰链力矩变化。文献[1]采用了自抗扰控制技术应用到电动舵系统中,基本思想是采用PD控制与扩张状态观测器相结合,取得了理想的控制效果。
在解决复杂的非线性系统问题时,滑模变结构作为一种综合方法得到了重视,具有很强的鲁棒性,其对系统参数摄动的不敏感是以控制量的高频抖动来换取的。系统要求电动舵机能在有限时间内跟踪指令,对于理想的被控对象,通常滑模控制[2]是通过选取合理的滑模面参数来保证状态空间任意位置运动点在有限时间内到达滑模面。针对高精度的伺服系统,实际存在很多的不确定项,且无法准确得知不确定项的上界。许多学者们提出了不同的方法对不确定干扰进行估计和辨识[3-5],算法涉及较多参数,调参复杂,实用性不强。文献[6]提出了使用扩张观测器估计电机负载转矩,使电机具有了更好的性能;文献[7]采用边界层与低通滤波器技术的滑模控制算法,同时对摩擦进行建模,在小角度时获得良好的跟踪效果,但对系统中的扰动只是假定上界,未能实时估计扰动。
本文针对电动舵机高精度伺服的特点,采用了扩张状态观测器对电动舵机运行中的负载扰动进行实时观测,提出了将线性扩张状态观测器与滑模变结构控制相结合,并给出了设计过程,最后通过仿真和实验对算法的合理性加以验证。
1 电动舵机的数学模型
电动舵机是控制飞行器舵面偏转的伺服系统,其主要由舵机控制器、功率驱动、伺服电机、传动结构和反馈传感器五部分组成,输入为舵控指令信号,结构组成如图1所示。

图1 电动舵系统结构框图Fig.1 Structure diagram of electromechanical actuator system
电动舵机控制器接收制导机给定的控制指令和传感器的反馈信号,计算出脉冲宽度调制(Pulse Width Modulation,PWM)控制信号。由驱动器驱动伺服电机,通过电机驱动减速传动机构带动舵面的偏转,舵面偏转角度经反馈电位计反馈至控制器形成闭环控制。
本文所涉及电动舵机经简化所得数学模型如图2所示。

图2 电动舵系统数学模型Fig.2 Mathematical model of electromechanical actuator system
其中:L为电机绕组电感;R为电机绕组电阻;Kt为电机力矩系数;J为舵机折算到电机轴的总转动惯量;Ki为电机到输出轴的传动比;Ke为电机反电动势系数;B为电机阻尼系数;TL为外加负载。
首先考虑被控对象,在开环条件下,由结构框图可以得到控制器输出到舵偏角的传递函数为:

(1)
电机模型中电气时间常数τe=L/R,机电时间常数τm=JR/(KtKe),由于其电气时间常数和电机阻尼较小,为方便研究,可以忽略,被控对象可以简化为:
(2)
将简化后的传递函数转化为微分方程形式,即为:
(3)
此微分方程表示了舵偏角与控制电压之间的关系,通过调节电压实现对舵机的控制。
2 滑模变结构控制器
滑模变结构控制[8]是一种非线性控制策略,它的控制特性迫使系统在进入滑动模态时沿着规定的状态轨迹作小幅度、高频率的运动,与系统的参数及扰动无关,滑模面是可设计的。针对如下被控对象:

(4)
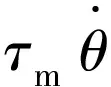
滑模面设计为:

(5)
其中,c>0且满足Hurwitz条件,e(t)=θd-θ,θd为期望指令信号。
由于滑模变结构控制存在高频抖动,为了抑制抖动,本文采用指数趋近律的方法。
指数趋近律表达式为:

(6)
(7)
由式(3)~式(6)可得,舵机的滑模控制律为:
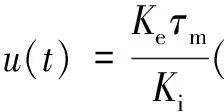
(8)
由于舵机实际运行中存在铰链力矩、伺服电机本身及传动机构间隙等非线性因素,且滑模函数的未知干扰d无法准确获得上界。为了对未知干扰实时估计并进行补偿,本文提出了采用扩张观测器的方法对不确定项进行补偿,把摩擦、负载等不确定因素等效为干扰进行补偿。
3 扩张状态观测器
扩张状态观测器(Extended State Observer,ESO)[9]是自抗扰控制器(Active Disturbance Reje-ction Control,ADRC)的核心部分,能对动态和不确定性的扰动进行综合估计。由于非线性扩展观测器参数较多,调节复杂,在实际应用中不能通过参数调节快速控制目标,所以本文采用线性扩张状态观测器对舵机不确定项进行估计[10]。
针对二阶被控对象式(3),考虑未知干扰d,转换为状态方程形式如下:
(9)

(10)

4 扩张状态观测器与滑模变结构复合的舵系统控制设计
本文涉及的电动舵机仅有电位计的反馈信号,采用位置闭环,其控制结果框图如图3所示。

图3 基于扩张状态观测器的滑模控制结构图Fig.3 Structure diagram of the sliding model control based on ESO
其中,ESO为三阶扩张状态观测器,输出的z2速度观测值作用到滑模变结构控制器,z3是由扩张状态观测器估计的总扰动量,补偿到控制器输出。
在实际舵系统的跟踪系统中,指令信号的频率比较低,采样频率达到了2kHz,所以指令信号的速度和加速度可以简化为零,由此可以得到电动舵机的实际控制器输出为:

(11)
5 仿真验证
实验样机的电动舵机参数如表1所示,滑模变结构控制器与扩张状态观测器各参数如表2所示。
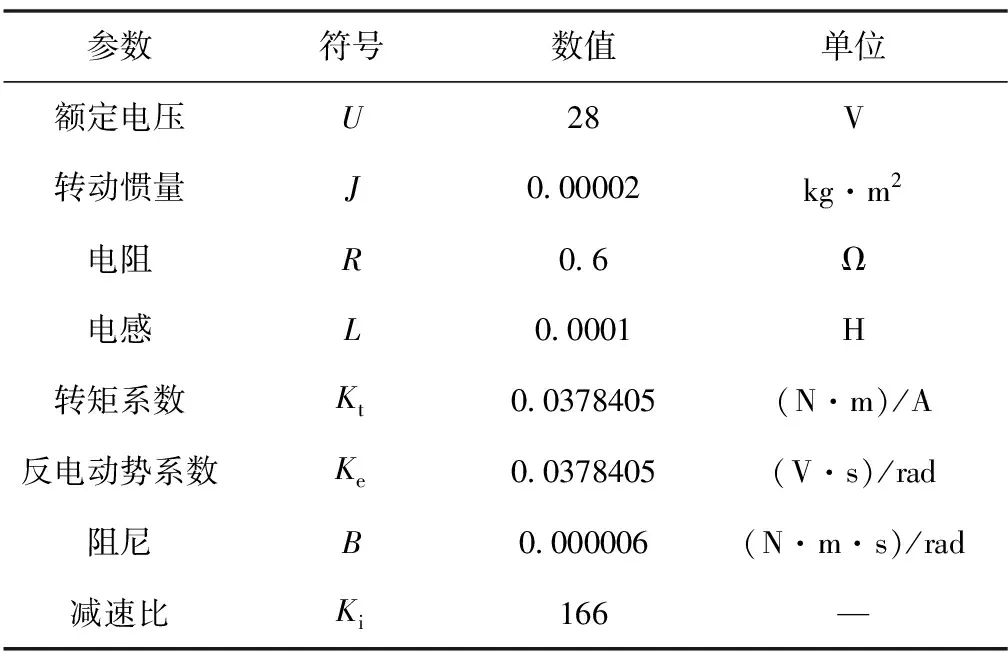
表1 电动舵机参数

表2 控制器各参数表
为了比较本文所提出的扩张状态观测器进行补偿的滑模变结构控制器与常规滑模变结构控制器的性能,对其进行仿真验证。
在Matlab/Simulink环境下,建立舵系统仿真模型。给定5V(10°)阶跃指令,施加4(N·m)/(°)的弹性负载,得到的仿真结果如图4所示。
仿真结果表明,给定大角度阶跃信号时,常规滑模变结构控制存在一定的静差,由于扩张观测器的存在,对负载进行观测,补偿到控制器中,可以有效减小静差,提高控制精度。
6 实验结果
为了验证仿真结果,在滑模控制器的参数保持不变的前提下进行样机实验。在4(N·m)/(°)弹性负载条件下,通过施加不同舵控指令来研究其控制算法的效果。图5所示为给定输入信号1V阶跃,得到两种算法的位置跟踪曲线。图6所示为给定输入5V阶跃的响应曲线。

图5 1V带载阶跃响应曲线Fig.5 1V step response with load

图6 5V带载阶跃响应曲线Fig.6 5V step response with load
从表3实验结果对比可知,系统到达目标位置后未出现超调现象,带扩张观测器的控制算法在小角度带载情况下与常规滑模控制算法作用效果差不多。常规滑模控制算法自身的抗干扰能力足以克服小角度时的负载扰动量,在大角度时,实验效果和仿真实验同样出现了一定的静差,而扩张观测器的作用则是缩小静差。

表3 实验结果对比
图7所示为小角度时1V,1Hz条件下施加4(N·m)/(°)弹性负载所得实际电动舵机正弦跟踪曲线。从图7中可以看出,本文提出的控制器能在速度过零时,跟踪误差明显减小。图8所示为实时观测器的补偿控制量,在过零点处补偿量最大,折算到控制信号占空比为5.5%。表明了本文提出的方法有效可行,使得电动舵机伺服控制得到进一步提高。
为验证大角度正弦位置跟踪效果,在弹性负载4(N·m)/(°)条件下,给定5V3Hz的舵控指令,实验跟踪效果曲线如图9所示,大角度时,在速度过零点处依然能够准确跟踪指令信号。观测器估计的干扰补偿量如图10所示。过零处补偿量折算到控制信号占空比达到17.5%。

图7 1V 1Hz位置跟踪曲线Fig.7 1V 1Hz position tracking

图8 1V 1Hz干扰补偿曲线Fig.8 1V 1Hz compensation cure of disturbance
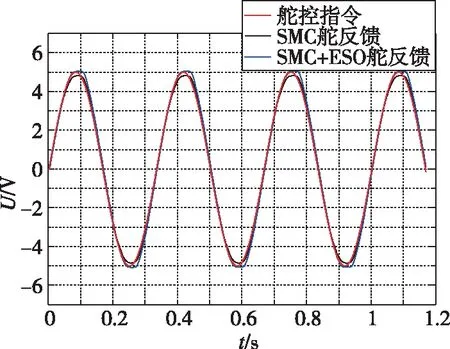
图9 5V 3Hz位置跟踪曲线Fig.9 5V 3Hz position tracking
7 结论
本文设计了滑模变结构与扩张观测器相结合的控制策略,通过扩张观测器观测电动舵机不确定模型因素和外加干扰,用于补偿其对系统的影响,在Simulink中验证算法的有效性。最终,通过某型电动舵机实物验证了算法的正确性和有效性。特别是针对在大负载情况下,补偿效果尤其明显,取得了很好的控制效果,具有很好的工程应用价值。

