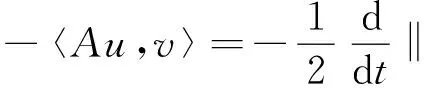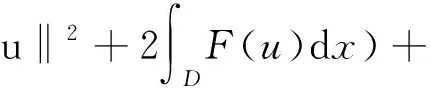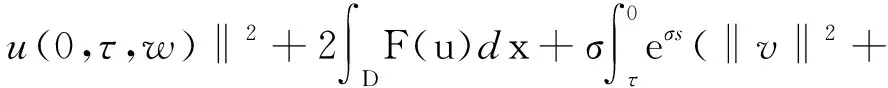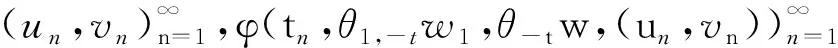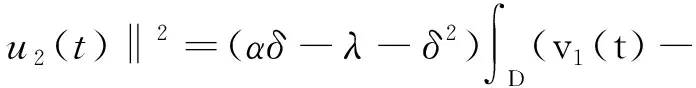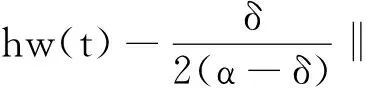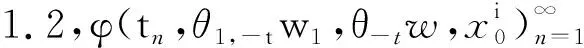一类非自治随机波动方程的随机吸引子

文慧霞, 舒 级, 李林芳

(四川师范大学 数学与软件科学学院, 四川 成都 610066)

1 引言及预备知识

设D⊂R3为具有光滑边界的有界区域，本文在D上考虑如下具加性噪声的非自治随机波动方程的长时间渐近行为

utt+αut-Δu+λu+f(u,t)=g(x,t)+

(1)

初边值条件为

u(x,τ)=u0(x),

ut(x,τ)=u1(x), x∈D,

(2)

u(x,t)=0, x∈∂D,t≥τ,

(3)

其中,α、λ是正常数，τ表示初始时刻，Δ是Laplace算子,w是一维双边标准Wiener过程，g(x,t)是时间依赖的外力项，非线性项f为R上光滑的具有立方增长率的函数.

波动方程是一类非常重要的偏微分方程,在物理学、流体力学、声学、电动力学等众多领域应用广泛.文献[1-4]对自治的随机波动方程证明了随机吸引子的存在性,文献[5-6]提出了压缩函数方法用于证明非自治系统的渐近紧性,文献[7-8]考虑了具可乘白噪音的非自治波动方程的渐近行为,文献[9]对有界区域上的非自治随机波动方程证明了随机吸引子的存在性.

随机吸引子是研究随机动力系统长时间渐近行为的有效工具，其实质是紧的不变集，该不变集依概率并随着时间变化.随机吸引子是对确定性动力系统中吸引子的推广[10].文献[11-12]给出了随机动力系统中随机吸引子的概念，并在文献[13-14]中作了详细阐述;文献[15]给出了对非自治无穷维动力系统和随机动力系统渐近行为的具体研究;文献[16-18]讨论了自治与非自治的反应扩散方程随机吸引子的相关问题;文献[19-20]则关注了格上的随机动力系统的渐近性质;文献[21-23]讨论了随机广义Ginzburg-Landau方程的渐近行为;文献[24-25]给出了一些KdV型方程随机吸引子的存在性证明.

本文的目的是证明(1)～(3)式在D上存在拉回吸引子.应用类似于文献[1-6]中的方法来解决这个问题.

下面给出非自治随机动力系统和随机吸引子的有关知识，具体参见文献[8,11,13].首先引进一些记号，用‖·‖和(·,·)表示Hilbert空间L2(D)的范数和内积.假设(X,‖·‖)是一个可分度量空间,B(X)为X的Borelσ-代数.

定义1.1设Ω是一个非空集合.如果一个映射θ:R×Ω→Ω满足:

(i)θ(0,·)为在Ω上的恒等映射IΩ;

(ii)θ(t+s,ω)=θ(t,θ(s,ω)),∀s,t∈R,ω∈Ω;

称θ为Ω上的一个动力系统.

定义1.2设θ1,θ2,,θr分别为集合Ω1,Ω2,,Ωr上的动力系统，X为一个拓扑空间.如果一个映射φ:R+×Ω1×Ω2××Ωr×X→X满足：

(i)φ(0,ω1,ω2,,ωr,x)=x,∀(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr;

(ii) 对∀s,t∈R,(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr,x∈X有

φ(t+s,ω1,ω2,,ωr,x)=φ(t,θ1(s,ω1),,

θr(s,ωr),φ(ω1,ω2,,ωr,x));

(iii) 对∀s,t∈R,(ω1,ω2,,ωr)∈Ω1,Ω2,,Ωr,x∈X,φ(t+s,ω1,ω2,,ωr,·)在X中连续,

则称φ为在X上的具有r个参数(ω1,ω2,,ωr)的关于参数动力系统θ1,θ2,,θr的动力系统.把Ωi(i=1,2,,r)叫做参数空间,(Ωi,θi)(i=1,2,,r)叫做参数动力系统.

对一个参数为随机参数的具有2个参数的动力系统，设(Ω2,F,P)是一个概率空间，保测映射φ2:R×Ω2→Ω2是一个关于σ-代数B(R×F;F)可测动力系统，即∀t∈R,P·θ2,t=P.动力系统(Ω2,θ2)叫做随机参数动力系统.设(Ω1,θ1)为任意一个随机参数动力系统.一个动力系统φ:R+×Ω1×Ω2×X→X,如果对∀ω1∈Ω1,φ(·,ω,·,·)关于(B(R+)×F×B(X);B(X))是可测映射，则称φ为随机动力系统.

定义1.3如果X的一个集族K=K(ω1,ω2):Ω1×Ω2→2X,(ω1,ω2)aK(ω1,ω2),对∀ω1∈Ω1,x∈X,映射ω2→(x,K(ω1,ω2))关于σ-代数(F;B(R+))是可测的，则称K为随机集族.

定义1.4称一个非空集族A=A(ω1,ω2)为随机动力系统φ的拉回吸收集.如果对任意有界集B⊂X,ω1∈Ω1,以及P-a.s.ω2∈Ω2,存在T=T(ω1,ω2;B)≥T时有

φ(t,θ1,-t(ω1),θ2,-t(ω2),B)⊂A(ω1,ω2),

其中,dist(·,·)表示X中的Hausdoff半度量.

定义1.5称一个非空集族A=A(ω1,ω2)关于φ的拉回吸引有界集B⊂X,如果对∀ω1∈Ω1,以及P-a.s.ω2∈Ω2有

A(ω1,ω2))=0.

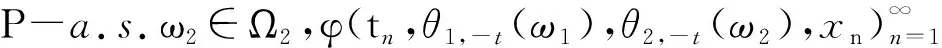
定义1.7如果一个随机紧集A=A(ω1,ω2)，对∀ω1∈ω1,以及P-a.s.ω2∈ω2满足:

(i)A关于φ拉回吸引X的任意有界闭集；

(ii)A关于φ随机不变集,也就是说，对∀t≥0,

φ(t,ω1,ω2,A(ω1,ω2))=

A(θ1,t(ω1),θ2,t(ω2)),

则称A为随机动力系统φ的一个随机吸引子.

定理1.1[26]定义于度量空间X上的连续随机动力系统φ，如果存在一个拉回吸收集B(ω1,ω2)，且φ在X中是渐近紧，那么φ拥有唯一的拉回吸引子A=A(ω1,ω2)为

A(ω1,ω2)=

定理1.2[5] 设定义于度量空间X上的连续随机动力系统φ存在一个拉回吸收集B(ω1,ω2)，对∀ε>0,ω1∈Ω1，以及P-a.s.ω2∈Ω2,存在T=T(ω1,ω2,ε)>0和压缩函数ψT，对∀(x,y)∈B(θ1,-t(ω1),θ2,-t(ω2))，当T

‖φ(T,θ1,-t(ω1),θ2,-t(ω2),x)-

φ(T,θ1,-t(ω1),θ2,-t(ω2),y)‖≤ε+ψT(x,y),

2 带加性噪声的非自治随机波动方程

由于w为完备概率空间(Ω2,F,P)中的一个独立双边实值Wiener过程，其轨道w(·)属于C(R,R)，且w(0)=0，在(Ω2,F,P)中的保测度转移算子定义为

θtw(·)=w(·,+t)-w(t),

w∈Ω2, t,s∈R,

那么(Ω2,F,P,(θt)t∈R)为一个度量动力系统.

对一较小的正数δ，引进新的变量z=ut+δu和v(t)=z(t)-hw(t),于是方程(1)～(3)变为只含随机参数的随机方程

(4)

其中，A=-Δ，v0=z0-hw(t)，z0=u1+δu0，x∈D.

为了得到方程弱解的存在性和拉回吸引子的存在性，需要对非线性项f施加条件：f∈C1(R×R,R)，并假设存在正常数C1,C2,C3,C4>0,对∀u∈R,t∈R满足:

|f(u,t)|≤C1(1+|u|3),

(5)

|f′(u,t)|≤C2(1+|u|2),

互联网时代，资源共享已经成为人们的共识，在此背景下，教师可以很轻松地通过网络搜索优秀的教案、课件和教学日志来完成备课，甚至还可以通过网络视频观看和学习其他优秀教师的教学方法。这就是“互联网+”时代资源共享给我们带来的好处。然而，有的教师却只会盲目照搬照抄这些网络教学资源，有的教师在教学过程中，离开信息技术无法上课，到了依赖的地步，把大量的时间和精力花费在对网络教育资源的收集和模仿上，从而丧失了自身独立思考和研究的能力，以至于成为信息技术的传话筒。这种忽视学生实际情况和教学环境的方式，不仅不能发挥出网络教育资源应有的作用，甚至还有可能起到反效果。

(6)

F(u,t)≥C3(|u|4-1),

(7)

uf(u,t)≥C4(F(u,t)-1),

(8)

θ1,t(f(·),g(·))=(f(t+·),g(t+·)),

t∈R,w1=(f,g)∈Ω1.

类似参考文献[10]中第IV章中定理5.1的证明，可得到如下定理.

注意，当选取δ满足λ+δ2-αδ≥0时，这一范数与如下范数是等价的

‖(u,v)‖X=(‖▽u‖2+

(9)

那么，在X上定义随机动力过程为φ(t,θ1,τw1,θτw,x0)=(u(t),v)∈X,u(t)是方程(4)中初始时间为τ的在τ+t时刻的解,其中w1(f(t),g(t))∈Ω1,w∈Ω2,x0=(u0,v0)∈X,那么由定理2.1可知，φ在X中关于参数动力系统θ1和θ构成随机动力系统.

3 随机吸引子的存在性

为了证明随机吸引子的存在性，首先给出解的先验估计，得到X中的随机吸收集.

引理3.1在定理2.1的假设条件下，随机动力过程φ在相空间X上存在随机吸收集.

证明这里需要估计

‖φ(t,θ1,τw1,θτw,x0)‖X

的值.为此，取w1=(f(u,t+τ),g(x,t+τ)).将方程(4)两边与v做内积得到

(δ-α)〈v,v〉+〈g(x,t),v〉-〈f(u,t),v〉+

(δ-α)〈h,v〉w(t).

(10)

δ‖u‖2-〈h,u〉w(t),

(11)

δ‖▽u‖2+〈▽h,▽u〉w(t),

(12)

δ〈f(u,t),u〉+〈f(u,t),h〉w(t),

(13)

则方程(10)变为

2(α-δ)‖v‖2+2δ(λ+δ2-αδ)‖u‖2+

2δ‖▽u‖2+2δ〈f(u,t),u〉=

2(λ+δ2-αδ)〈h,u〉w(t)+2〈▽u,▽h〉w(t)+

2〈f(u,t),h〉w(t)+2〈g,v〉+

2(δ-α)〈h,v〉w(t).

(14)

由(8)式可得

2δ〈f(u,t),u〉≥

(15)

由(5)与(7)式可得

2C1‖h‖|w(t)|+

2C1‖h‖|w(t)|+

(16)

利用Young和Holder不等式处理余下几项可得

2(λ+δ2-αδ)〈h,u〉w(t)≤

(λ+δ2-αδ)‖u‖2+

C‖h‖2|w(t)|2,

(17)

2〈▽u,▽h〉w(t)≤δ‖▽u‖2+

C‖▽h‖2|w(t)|2,

(18)

2|〈g,v〉|+2|(δ-α)〈h,v〉w(t)|≤

(α-δ)‖v‖2+C‖h‖2|w(t)|2+

C‖g‖2.

(19)

C3(2σ-δC4)|D|.

(20)

由(8)式得

▽u‖2+

σ(‖v‖2+(λ+δ2-αδ)‖u‖2)≤

C(1+|w(t)|2+|w(t)|4).

(21)

由Gronwall不等式可得

‖v(0,τ,w)‖2+(λ+δ2-αδ)‖u(0,τ,w)‖2+

(λ+δ2-αδ)‖u‖2+‖▽u‖2)ds≤

eστ(‖v0‖2+(λ+δ2-αδ)‖u0‖2+

|w(s)|4)ds.

(22)

由范数‖·‖X的等价定义(9)式,综合(7)式得

‖φ(t,θ1,τw1,θτw,x0)‖X≤eστ(‖v0‖2+

(λ+δ2-αδ)‖u0‖2+‖▽u0‖2+

|w(s)|4)ds+C|D|.

(23)

于是当-t→0即τ→-∞时，上式右端第一项趋近于0.又因为w(t)至多多项式增长，所以上式右端第二项有界.令

|w(s)|4)ds+C|D|,

那么从(23)式可知，随机集

B(w1,w)={x∈X,‖x‖X≤R(w1,w)}

是φ的一个拉回吸收集.进一步，有下面的渐近紧性.

u2(t))+(Δu1(t)-δu2(t))+(δ-α)(v1(t)-

v2(t))-(f1(t)-f2(t)).

(24)

定义能量函数为

用v1(t)-v2(t)对上式两端做内积，由

可得

▽u1(t)-

v2(t))(u1(t)-u2(t))dx-δ‖▽u1(t)-

▽u2(t)‖2+〈▽u1(t)-▽u2(t),▽h〉w(t)+

(δ-α)〈v1(t)-v2(t),v1(t)-v2(t)〉-

〈f1(t)-f2(t),v1(t)-v2(t)〉.

(25)

对(25)式t在[s,T]上积分

又因为E0(T)≥0，所以

v2(t))dxdt+Ew(s).

(27)

用u1(t)-u2(t)乘(24)式两端，并在[τ,T]×D上积分得

(δ-α)(v1(t)-v2(t))(u1(t)-u2(t))-

(f1(t)-f2(t))(u1(t)-u2(t)))dxdt.

(28)

对(26)式关于s在[τ,T]上积分可得

(T-τ)E0(T)=

(v1(t)-v2(t))(u1(t)-u2(t))+

(▽u1(t)-▽u2(t))▽hw(t)]dx+

(δ-α)‖v1(t)-v2(t)‖2-

δ‖▽u1(t)-▽u2(t)‖2-

(29)

结合(27)～(29)式可得

(v1(t)-v2(t))(u1(t)-u2(t))+

(▽u1(t)-▽u2(t))▽hw(t)]dx+

(δ-α)‖v1(t)-v2(t)‖2-

δ‖▽u1(t)-▽u2(t)‖2-

(v1(t)-v2(t))(u1(t)-u2(t))dxdt+

(v1(t)-v2(t))(u1(t)-u2(t))+

‖▽u1(t)-▽u2(t)‖‖▽hw(t)‖]dx+

(δ-α)‖v1(t)-v2(t)‖2)dtds+

(v1(t)-v2(t))(u1(t)-u2(t))dxdt+

上式右端除了最后2行其余部分定义为压缩函数ψT，则有

于是，对任意的ε>0，存在充分大的T-τ，使得

‖(un(t),vn(t))‖X<+∞,

∀t∈[τ,∞), n∈N.

由弱拓扑的紧性，得到

un⇀u在L∞([τ,∞);H01(D))中弱*收敛，

vn⇀v在L∞([τ,∞);L2(D))中弱*收敛，

un→u在L2([τ,∞);L2(D))中强收敛，

un(τ)→u0,un(T)→u(T)在L4中强收敛. (30)

因此，unt=vn-δun+hw(t)在L∞([τ,∞);L2(D))中弱收敛于ut=v-δu+hw(t)，从(30)式中可知

(u1(T)-u2(T))dx=0,

(unt(t)-umt(t))dx=0,

(un(t)-um(t))dx=0.

利用非线性条件(6)和(7)式得

(unt(t)-umt(t))dxdt=

其中

由(7)和(30)式可得

所以可得

(un(t)-um(t))dxdt=0.

又利用柯西不等式，存在一个常数C5,

▽u1(t)-▽u2(t)‖×

‖▽hw(t)‖dtds≤

从而得

▽u1(t)-

▽u2(t)‖‖▽hw(t)‖dtds=0.

同样也可找到一个合适的常数C6,

所以有

‖v1(t)-v2(t)‖2dtds=0.

最后，结合定理1.1、引理3.1和引理3.2，可得随机吸引子的存在性.