非线性项带导数的三点边值问题正解的 存在性与多解性
康宏亮, 肖鸿民
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
1 引言及主要结果
基于丰富的实际应用背景,非线性常微分方程边值问题正解的存在性和多解性问题在常微分方程研究领域显得尤为重要.对于经典的三点边值问题,近30年来已取得了一定结果,参见文献[1-15]及其相关文献.
特别地,1994年,Wang[1]在f∈C([0,∞),[0,∞)),a∈C([0,1),[0,∞))且a(t)在(0,1)的任意子区间内不恒为0的条件下构造锥
K={u(t):u∈C[0,1],u(t)≥0,
然后运用锥上的不动点理论获得了二阶微分方程Robin边值问题
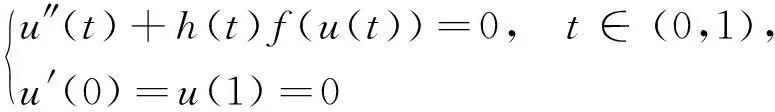
(1)
在非线性项满足超线性或次线性条件下其正解的存在性.
1999年,Ma[2]研究三点边值问题

时提出了研究这类问题的关键条件
0<αη<1,
并且通过构造锥
K={u∈C[0,1]:u(t)≥0,
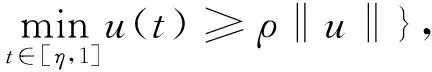
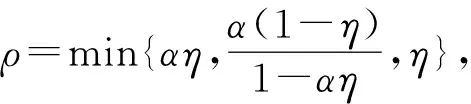
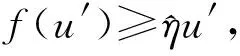
文献[1-2]中的f均不依赖于u′,因为f(u′)在C[0,1]内研究,将无法构造锥,继而无法运用锥上的不动点定理研究相应问题正解的存在性.但经过仔细分析发现,对于边界条件比较特别的形式而言,当非线性项上带导数时,可以在C1[0,1]中构造锥,进而使用不动点指数理论获得该问题正解的存在性和多解性.基于此,本文将研究系统

正解的存在性和多解性,其中,α>0,0<αη<1.
本文总假定:
(H1)f:[0,∞)→[0,∞)连续;
(H2)a∈C([0,1],[0,∞))且在(0,1)的任意子区间内a(t)不恒为0;
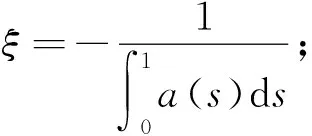

本文主要结果如下:
定理1假定(H1)和(H2)成立,若f满足下列条件之一:
(i) (超线性)f0=0且f∞=∞;
(ii) (次线性)f0=∞且f∞=0,
则边值问题(3)至少存在一个正解,其中
定理2假定(H1)~(H3)成立且f0=f∞=∞,那么问题(3)至少存在2个正解x1、x2,使得
0<‖x1‖ 定理3假定(H1)、(H2)和(H4)成立且f0=f∞=0,那么问题(3)至少存在2个正解x1、x2,使得 0<‖x1‖ 本文主要工具为: 引理1[16]设X为Banach空间,K⊆X是X中的一个锥.定义Kp={x∈K|‖x‖≤p,p>0},∂Kp={x∈K|‖x‖=p},假设A:Kp→K是一个全连续算子,当x∈∂Kp时Ax≠x,则: (i) 如果当x∈∂Kp时,有‖x‖≤‖Ax‖成立,则i(A,Kp,K)=0; (ii) 如果当x∈∂Kp时,有‖x‖≥‖Ax‖成立,则i(A,Kp,K)=1. 引理2[15]设α≠1,则对y∈C[0,1],问题 (4) 有唯一解 u∈[0,1], 其中 因此Hammerstein积分算子的核为 其中 且 引理3A(K)⊆K,且A是全连续算子. 证明 u″(t)=-a(t)f(u′(t))≤0. 故A(K)⊆K.由f的连续性及Arzela-Ascoli定理可知A:K→K是全连续算子. 定理1的证明定义锥K={u∈C1[0,1],u′≤0,u在[0,1]上是向上凸的,u′(0)=0,u(1)=αu(η)}. 容易验证锥K中的元素u满足 (5) 这里 (i) 超线性情形.因为f0=0,取H1<0,使得对H1≤u′≤0,有f(u′)≤ηu′,其中η<0满足 因此若u∈K,‖u‖=-H1,则由 记 Ω1:={u∈X:‖u‖≤-H1}, 则 ‖Au‖≤‖u‖,u∈K∩∂Ω1. 故 ‖Au‖≥‖u‖,u∈K∩∂Ω2. 记 Ω1:={u∈X:‖u‖<-H1}, 则 ‖Au‖≥‖u‖,u∈K∩∂Ω1. 所以‖Au‖≤‖u‖. 所以无论何种情况,只要令Ω2:={u∈X:‖u‖<-H2},就有‖Au‖≤‖u‖,u∈K∩∂Ω2.由引理1(ii)知问题(3)有一个正解. 定理2的证明令M<0,使得 (6) 由f0=f∞=∞与引理1(ii)知,若存在p 因此,由引理1得 i(A,Kr,K)=0. (7) 对同样的满足(6)式的M,由f0=f∞=∞可知,存在R1<0,使得f(u′)≥Mu′,∀u′≤R1.令R 因此,由引理1得 i(A,KR,K)=0. (8) 另一方面,由条件(H3),若u′∈∂Kp,则 因此,由引理1得 i(A,Kp,K)=1. (9) 由(7)~(9)式得 i(A,KRKp,K)=-1,i(A,KpKr,K)=1. 因此,A在KRKp上有一个不动点x1,在KpKr上有一个不动点x2,均为问题(3)的解,并且x1(t)>0,x2(t)>0,t∈(0,1). 定理3的证明由f0=f∞=0,对∀ε<0,存在W<0,使得f(u′)≤W+εu′,∀u′≤0,t∈[0,1],那么 因此,令ε充分小且R i(A,KR,K)=1. (10) 同样地,对p i(A,Kr,K)=1. (11) 另一方面,由(H4),对u′∈∂Kp有 因此,由引理1得 i(A,Kp,K)=0. (12) 由(10)~(12)式得A有2个不动点,则问题(3)有2个正解. 例1考虑非线性项带导数的二阶三点边值问题 满足超线性情形,则由定理1可知,问题(13)至少存在一个正解.


2 主要结果的证明
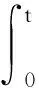
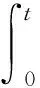
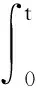

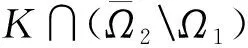

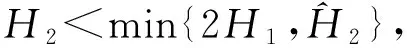

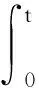
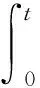
3 应用


