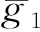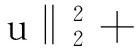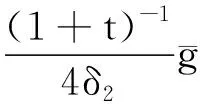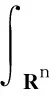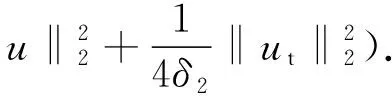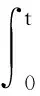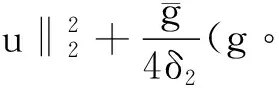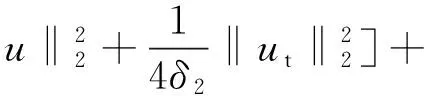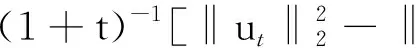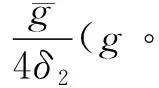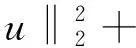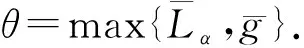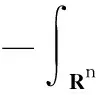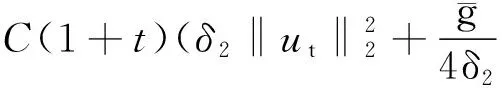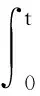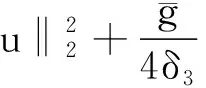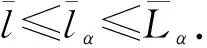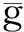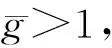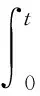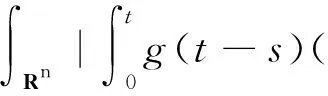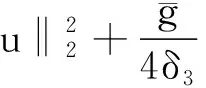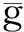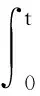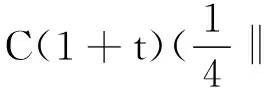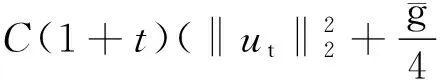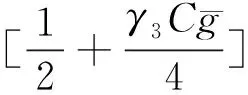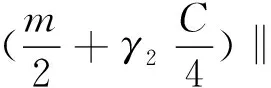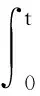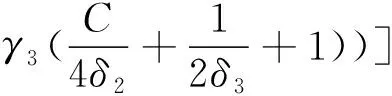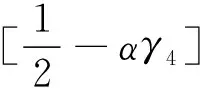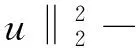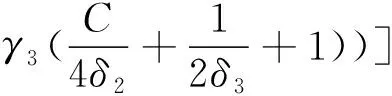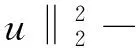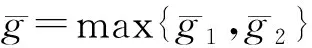带有记忆核的黏弹性方程解的能量衰减估计
李 娜, 蒲志林
(四川师范大学 数学与软件科学学院, 四川 成都 610066)
1 引言与预备知识
本文考虑以下带有记忆项的黏弹性方程的柯西问题
(1)
其中,u0和u1是给定的初始函数,g是定义在Rn上正的非递增函数,g称为记忆核.这类问题出现在黏弹性问题中,特别是带有衰减记忆的热力学材料中.Coleman等[1-2]早期工作中都有涉及到这类问题.
许多文献研究了在有界区域上的此类问题的处理.大致上,这类问题可以概述为,当记忆函数g是指数(多项式)衰减,则解呈指数(多项式)衰减.然而在之前所有的工作中,关于(非负)记忆核都有如下的假设:
g(0)>0,g′(t)≤-γg(t), ∀t≥0,
(2)
其中γ>0.上述假设条件太严格,已有许多文献讨论放宽这一假设,例如文献[3-5].特别地,当g(0)>0,g′(t)+γg(t)≥0时,其中t≥0,γ>0且在[g′(t)+γg(t)]eαt∈L1(0,∞),α>0条件下证明了当时间无限大时,方程的解呈指数衰减到零.在这个假设中,g′(t)可以取非负值,即g(t)是振荡函数.在Rn空间中,对g的一阶二阶导数的进一步规定下,Noz等[6]已经证明了解呈多项式衰减,且记忆函数g可以取负值.
本文的目的是研究方程(1)解的渐近性.基于文献[4],将有界区域扩展到Rn空间中,从而得到衰减结果.值得注意的是本文中,如Poincaré不等式、嵌入不等式等都不再是固定的.很自然会面临一些困难,特别是文献[4]中使用的泛函在此文中不能使用,需要使用另外的技巧.
在方程(1)中,g是方程的记忆核,通常它满足以下假设[7]:
(H1)g:R+→R+是一个可微函数,满足

(H2) 存在α>0,有
g′(t)+αg(t)≥0,t≥0,
(t+1)α[g′(t)+2αg(t)]∈L1(R+).
α>1后文会具体给出.
注1.1存在满足(H1)和(H2)的松弛函数g,只要选择合适的a、b即可,例如
与文献[6]相比,本文的假设与证明过程是不同的,而且衰减也是更慢的.
引理1.1[3]若假设(H1)和(H2)成立,且
u0∈H1(Rn), u1∈L2(Rn),
则方程(1)存在唯一解满足
u∈C([0,∞),H1(Rn)),
ut∈C([0,∞),L2(Rn)).
引理1.2[3]当1≤p 而且,存在一个常数C=C(n,p),使得 ‖u‖p*≤C‖▽u‖p, ∀u∈W1,P(Rn). 引理1.3若u是方程(1)的解,则 ‖u(t)‖2≤C(L+t)‖▽u(t)‖2,t>0, (3) 其中L是正常数. 证明由引理1.1,当p=2时,可得 由Hölder不等式可得 其中L>0,满足 Supp{u0(x),u1(x)}⊂B(L)= {x∈Rn/|x| 因此 ‖u(t)‖2≤C(L+t)‖u(t)‖p*≤ C(L+t)‖▽u(t)‖2. 引理1.3得证. 不失一般性,下文令L=1.现在,定义能量泛函 其中 v(t)|2dxds, ∀v∈L2(Rn). 引理1.4若u是方程(1)的解,则能量方程满足 (4) 证明对方程(1)两侧同乘ut,然后在Rn上积分.通过分步积分和重复文献[5,7]的工作,整理后就能得到结果.值得注意的是此时的E′(t)不确定正负,并且在这一步也不能确定系统是否耗散. 在下文中作如下的标记: l(t)=g′(t)+αg(t), Lα(t)=(t+1)α[g′(t)+2αg(t)]. 下面先建立若干引理,然后得到方程(1)的解的能量衰减估计. 引理2.1假设(H1)和(H2)成立,构造辅助泛函 |u(t)-u(s)|2dsdx, 其中 则对于任意δ1>0和t≥0有 (5) 证明利用假设(H2)和分部积分法得到 下面对Φ1(t)求导,并用Young不等式得到 α(1+t))-1Φ1(t)+ (1+t)-1[-((l+αg)∘u)+ -(1+t)-1Φ1(t)-α(1+t))-1Φ1(t)+ (1+t)-1[-((l+αg)∘u)+ 引理2.2若u是系统(1)的解,定义辅助泛函 在假设(H1)和(H2)条件下,则对于任意的δ2>0,t≥0有 (6) 证明对Φ2(t)求导可得 (7) 由(1)式可得 ▽u|2dx+ (8) 利用(3)式可得 C(1+t)‖▽u‖2‖ut‖2≤ (9) 同理可得 最后,结合(6)~(10)式得到 引理2.3若u是系统(1)的解,定义辅助泛函 (u(t)-u(s))dsdx, 则对于任意的δ2,δ3>0,t≥0满足 (11) 证明直接对Φ3(t)求导可得 (u(t)-u(s))dsdx- (12) 对于(12)式中的第二项,由(1)式可得 (▽u(t)-▽u(s))ds)dx. (13) 对于(13)式中的第一项有 (14) 对于(13)式中的第二项有下面的估计 (15) 与 ▽u(t)-▽u(s))ds|2dx≤ (▽u(t)-▽u(s))ds)dx≤ |▽u(t)-▽u(s)|dsdx+ (17) 联立(12)~(17)式,则(11)式成立. 引理2.4假设(H1)和(H2)成立,构造辅助泛函 (18) 其中 当取合适的2个正常数ξ1和ξ2,则满足 ξ1E(t)≤F(t)≤ξ2[E(t)+Φ1(t)], t≥t0, (19) 其中t0是足够大的值,使得γ2、γ3和γ4充分小. 证明由Cauchy-Schwarz不等式、Young不等式和(3)式可得 (20) 和 (21) 下面将(20)和(21)式带入F(t),可得 ξ2[E(t)+Φ1(t)],ξ2>0. (22) 又 |F(t)-E(t)|= 其中γ1、γ2、γ3和γ4充分小,则得到 F(t)≥ξ1E(t),t≥t0,ξ1>0. (23) 联立(22)和(23)式得到结论. 引理2.1假设(H1)和(H2)成立,且u0∈H1(Rn),u1∈L2(Rn),则存在2个正常数K和k,使得 E(t)≤K(1+t)-k, t≥0. 证明对(18)式求导,利用(4)式可得 (g′∘▽u). (24) 因为g是连续且g(0)>0,所以对任意的t≥t0≥tm>0有 再将(5)、(6)和(11)式带入(24)式 g′(t)=l(t)-αg(t)≤ l(t)-α(1+t)-1g(t), 可得 F′(t)≤-(1+t)-1[1+α- (1+t)-1{γ2(m-δ2(C+1))- (1+t)-1[γ3(g0-δ2(α+C+1))- (25) 现在令γ4=1,可得 F′(t)≤-(1+t)-1[1+α- (1+t)-1{γ2(m-δ2(C+1))- (1+t)-1[γ3(g0-δ2(α+C+1))- (26) 进一步,选择合适的δ2和δ3使得 若δ2和δ3固定了,选择任意合适的γ2和γ3满足下列条件 (27) 这样使得 γ3(g0-δ2(α+C+1))- γ2(m-δ2(C+1))-2γ3δ3=k2>0. 因此,若选择的γ2和γ3足够小使得(26)和(27)式成立,则进一步得到 现在,选择足够大的γ1使得 再令δ1满足下面的条件 则有下面的式子成立 k1-γ1δ1>0. 最后,当c>0和t≥t0时,就使得(26)式变为 F′(t)≤-c(1+t)-1[E(t)+Φ1(t)]≤ (28) 对(28)式在(t0,t)上积分后得到 最后由(19)式即证得结论.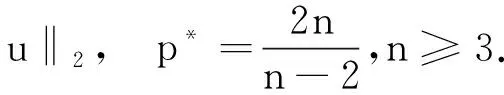

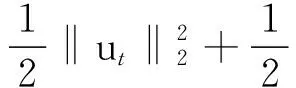
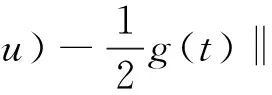

2 能量衰减估计