地下叠合墙接触面形式的设计研究
于 勇, 李腾飞, 马军秋, 于艺林, 田 辉
(1. 中铁第六勘察设计院集团有限公司, 天津 300000; 2. 中建市政工程有限公司, 北京 100071)
0 引言
近年来,随着城市地下工程的不断发展,深大基坑[1-3]越来越多。地下连续墙作为围护结构形式的一种,因其地层适应性强、施工安全性高等特点,现已逐渐成为复杂地层中深大基坑的首选围护结构形式; 此外,若能将其作为主体结构内衬墙的一部分[4-7],既能节约工程投资造价,提高施工效率,又具有整体性能好等优点。在未来的地下工程领域,叠合结构[8]将拥有更加广阔的运用前景。国内学者对叠合结构进行了很多有意义的研究工作,洪炳钦等[9]对叠合梁斜截面抗剪性能开展了试验研究,得到了其变形规律;刘文春等[10]运用ANSYS软件从理论方面研究了叠合梁的抗剪性能,分析了叠合梁的典型特征;李晓春[11]为研究纬三路过江通道工作井的全过程工作形态,分析了叠合墙结构体系的合理性。以上学者针对叠合结构受力特性以及力学行为等方面开展了大量工作,但在叠合结构施工以及叠合构造方面还缺乏一定的研究。
叠合结构施工通常在已完成施工的结构接触面上采用机械凿毛或设置钢筋接驳器等方式进行前期处理,后期与现浇混凝土浇筑成整体,接触面的预处理措施则主要起到剪力传递的目的。但因其接触面预处理施工难度大、工期长、剪力槽设置参差不齐等原因,叠合结构在实际运用过程中效果并不理想。
因此,本文针对上述问题提出一种便于施工的预制叠合结构形式,运用ANSYS有限元软件对波浪形、三角形以及梯形波纹结构面进行模拟受力分析,通过结果对比选出一种受力良好的结构面作为叠合结构的剪力槽,然后对采用该剪力槽的叠合结构、未采用该剪力槽的平面叠合结构以及现浇整体结构通过现场静力荷载试验分析研究其变形协调性、力学行为和变形规律,以期为城市地下工程的设计和进一步的理论研究提供参考和借鉴。
1 叠合面形式的有限元分析
本文对波浪形、三角形以及梯形波纹结构面选取3组较为常见的典型尺寸,并采用ANSYS有限元软件进行受力分析,通过分析结果对比为后续现场静力荷载试验提供依据。
1.1 计算模型及单元选取
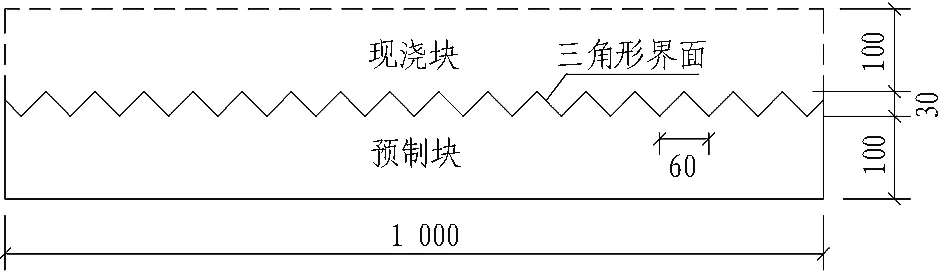
本次模拟计算分析模型共3组,分别记为A-1、A-2、A-3,水平向模型长度为1.0 m,剪力槽高度均为30 mm。具体结构模型尺寸如图1所示。

(a) A-1模型
(b) A-2模型
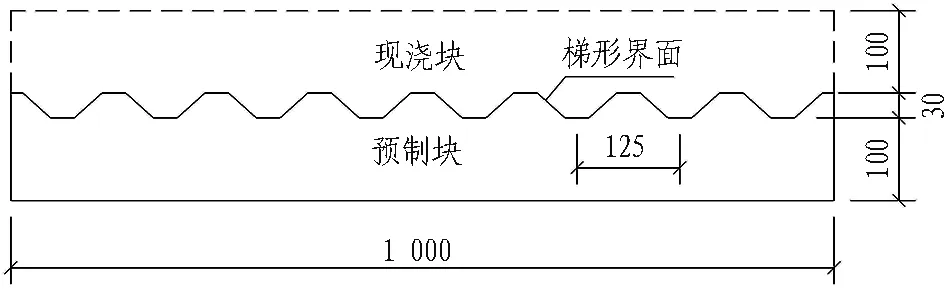
(c) A-3模型
计算模型为二维结构荷载横断面模型,采用8节点PLANE183单元进行模拟,材料本构关系为线弹性。在本次模拟过程中仅对不同类型结构面形式在受到剪切力的作用下进行受力及变形分析,预制板与现浇板接触面摩擦因数取值均为0.5,忽略实际施工过程中新旧混凝土接触面的差异性以及材料自身等因素。具体计算参数如表1所示。

表1 模型参数表
1.2 模型边界条件以及荷载
结构模型的边界条件为: 预制板底面(非接触面)边界施加水平方向以及竖直方向上的固定约束,现浇板顶面(非接触面)施加竖直方向上的约束力。有限元计算模型如图2所示。

图2 有限元计算模型图
为了更好地对比上述3类接触面的受力情况,对A-1、A-2、A-3模型现浇块分别施加5组水平向面节点荷载,分析其受力结果,5组荷载依次为5、10、20、50、100 kN。
1.3 模拟结果与分析
1.3.1 结构应力分析
图3示出模型结构应力模拟结果。由图3可知: 3组结构模型在初始阶段均表现为线性变化,应力最大值随施加切向荷载的增大而增大,A-1组模型在荷载增大至50 kN后存在一个明显的拐点,增大幅度降低,最大值达到2.56×106kN; A-2和A-3组模型结构应力均小于A-1组,最大值分别为1.94×106kN和2.45×106kN。同时,根据应力云图可知: A-2组模型预制块整体结构应力增长较大; A-3组模型仅在接触面处存在结构应力集中现象,其他区域应力较小。
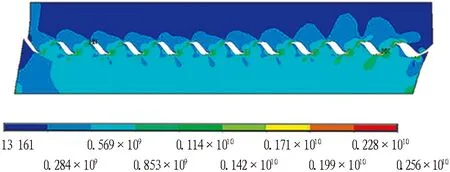
(a) A-1模型结构应力云图(单位: N)

(b) A-2模型结构应力云图(单位: N)
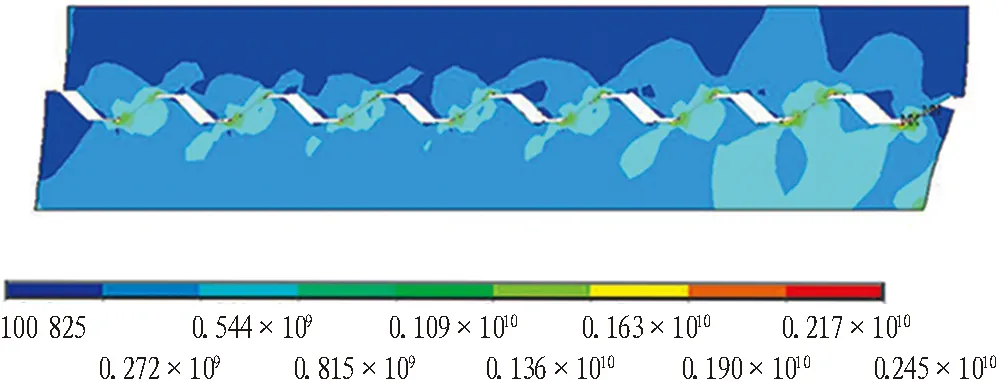
(c) A-3模型结构应力云图(单位: N)
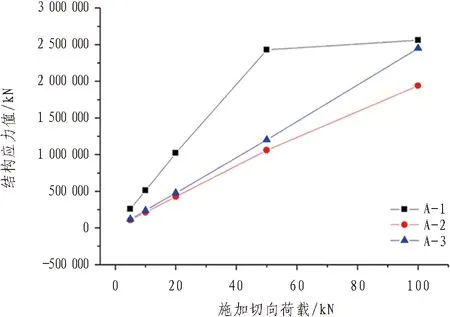
(d) 模型应力变化统计图
1.3.2 接触面压力分析
图4示出模型结构接触面压力模拟结果。由图4可知: 与结构应力模拟结果基本相同,接触面压力最大值随施加切向荷载的增大而增大,A-1组模型在荷载增大至50 kN后存在一个明显的拐点,增大幅度降低,最大值达到1.14×106kN; A-2和A-3组模型接触面压力均小于A-1组,最大值分别为6.09×105kN和6.59×105kN。同时,根据应力云图可知: A-2组模型在接触面存在多处应力集中现象; A-1和A-3组模型接触面压力仅在2处达到最大值,其他区域压力均小于最大值。
(a) A-1模型接触面压力云图(单位: N)

(c) A-3模型接触面压力云图(单位: N)
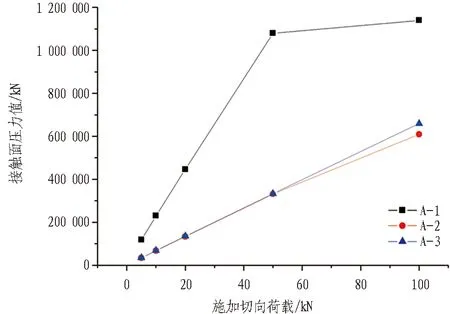
(d) 模型接触面压力变化统计图
1.3.3 接触面滑移分析
图5示出模型接触面滑移量模拟结果。由图5可知: A-1组模型接触面滑移量增长最快,最大值达到2.84×10-3mm; A-2和A-3组接触面滑移量最大值分别为2.628×10-3mm和1.791×10-3mm。A-1组模型在荷载增大至50 kN后存在一个明显的拐点,之后呈水平状,由此推断A-1组模型接触面摩阻力此时已基本达到最大值; A-2组模型在荷载增大至50 kN后存在一个小幅度的拐点,接触面滑移量基本表现为线性增加; A-3组模型呈现出良好的线性变化。

(a) A-1模型接触面滑移量云图(单位: m)

(b) A-2模型接触面滑移量云图(单位: m)

(c) A-3模型接触面滑移量云图(单位: m)

(d) 模型接触面滑移量变化统计图
根据以上模拟结果对比可知,A-3组模型在结构应力、接触面压力以及接触面滑移方面明显优于A-1、A-2组,其结构模型受力更加明确、合理,滑移量更小;同时,考虑到叠合面混凝土在浇筑以及施工过程中A-2组模型存在浇筑不密实以及后期施工易产生破损等问题,确定A-3组模型(梯形波纹结构)作为后续叠合结构静力试验对象。
2 叠合结构静力荷载试验
2.1 模型设计
本次静力结构荷载试验共制作2块钢筋混凝土梁,钢筋混凝土整体现浇梁(简称为整浇梁)记为L1,尺寸为3 380 mm×660 mm×400 mm,几何模型见图6;叠合梁记为L2,其中预制钢筋混凝土部分(记为L2(下))尺寸为3 380 mm×660 mm×200 mm,叠合面采用A-3梯形模型,现浇钢筋混凝土部分(记为L2(上))尺寸为3 380 mm×660 mm×200 mm,几何模型见图7。2块梁短边(660 mm)方向设置5根φ12 mm HRB400钢筋,长边(3 380 mm)方向设置23根φ8 mm HPB300箍筋,混凝土强度等级为C30。

图6 钢筋混凝土整体现浇梁(L1)几何模型图(单位: mm)
Fig. 6 Geometric model of reinforced concrete cast-in-place beam(L1) (unit: mm)

图7 钢筋混凝土叠合梁(L2)几何模型图(单位: mm)
Fig. 7 Geometric model of reinforced concrete composite beam(L2) (unit: mm)
叠合面处理措施:首先,在预制叠合梁钢筋绑扎阶段,将梯形波纹钢板每间隔20 cm钻1 cm左右小孔; 然后,采用扎丝将波纹钢板与纵向钢筋进行绑扎固定,同时预留足够的保护层厚度; 最后,浇筑混凝土时,波纹钢板作为叠合面一侧模板,待预制梁达到强度后进行剥离,即形成梯形叠合面。叠合梁现场施工如图8所示。

(a)

(b)
图8 A-3模型叠合梁现场施工图
Fig. 8 Site construction drawings of model A-3 composite beam
2.2 试验内容
本次试验加载及测定方式如图9所示。在梁跨中两侧0.7 m位置竖向方向上施加2个集中荷载,荷载采用千斤顶进行施加,每级荷载P=20 kN,之后逐级进行加载,持续时间为10 min,待结构变形稳定后,依次读取所需测量数据进行对比分析。

图9 试验梁静力加载及测定方案设计图(单位: mm)
Fig. 9 Design drawing of static load and measurement scheme of model beam (unit: mm)
试验主要测定内容包括: 1)测定整浇梁L1与叠合梁L2跨中在每级荷载作用下的挠度变化; 2)测定整浇梁L1与叠合梁L2中间位置的水平位移变化情况; 3)观察裂缝开始发生以及持续发展的变化情况。
试验测定标准: 当试验梁在荷载施加作用下产生的最大裂缝宽度达到0.2 mm或跨中挠度达到3 000/200=15 mm时,认为梁已达到正常使用极限状态;当梁的挠度达到3 000/50=60 mm时,认为梁已达到承载能力极限状态。本次结构静力荷载试验所施加荷载主要以结构达到正常使用极限状态作为重点分析。
2.3 试验结果
2.3.1 挠度分析
本次试验得到的试验梁挠度的荷载-变形曲线如图10所示。由图10可知: 当施加荷载小于250 kN时,整浇梁L1与叠合梁L2挠度曲线基本呈水平状,两者未出现明显的变形,但由于叠合梁L2存在剪应力超前的原因,挠度变化量稍大于整浇梁;当荷载继续增加时,整浇梁L1与叠合梁L2的挠度均呈现出增大的趋势,根据现场观测发现,整浇梁L1在荷载施加至300 kN、叠合梁L2在荷载施加至260 kN时,两者截面出现了第1条裂缝;之后,荷载继续增加,叠合梁L2在荷载施加至320 kN时,挠度增长率出现了一个小的突变现象,这是由于叠合梁L2中间的叠合面两侧所配置的钢筋承受了一部分荷载,抑制了梁的弯曲变形作用,而整浇梁L1挠度变化则呈现较为平顺的增长曲线; 荷载施加至500 kN时,两者挠度均已超过正常使用极限状态下的15 mm,整浇梁L1最终挠度达到22.51 mm,叠合梁L2达到20.62 mm。
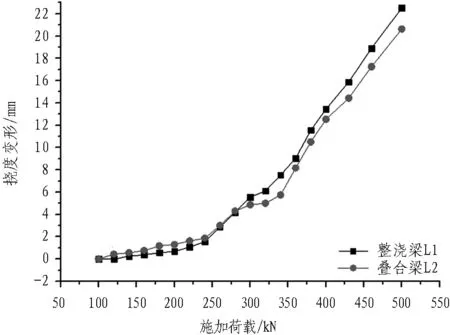
图10试验梁不同荷载作用下挠度曲线
Fig. 10 Deflection curves of test beam under different loads
2.3.2 水平位移分析
本次试验得到的试验梁水平位移的荷载-变形曲线如图11所示。由图11可知,当施加荷载小于300 kN时,整浇梁L1与叠合梁L2水平位移曲线大致呈水平状,两者未出现明显的水平位移,但整浇梁L1与叠合梁L2(下)的水平位移基本一致,而叠合梁L2(上)则明显小于前两者;当荷载继续增加,叠合梁L2在 320 kN荷载作用下,下部分预制结构水平位移变化量突然增大,此时也正是叠合梁L2产生裂缝的阶段,说明叠合梁L2(上)与叠合梁L2(下)在出现裂缝时彼此间也存在一个明显的错动滑移现象,叠合面两侧所配置的钢筋对水平位移起到了一定的抑制作用;当荷载施加至500 kN时,整浇梁L1最终水平位移达到1.25 mm,叠合梁L2(上)达到1.19 mm,叠合梁L2(下)达到0.81 mm。整浇梁L1与叠合梁L2(上)水平位移量基本一致(相差5%),而叠合梁(下)由于错动滑移,水平位移明显小于前两者(分别相差46.9%和54.3%)。

图11 试验梁不同荷载作用下水平位移曲线
Fig. 11 Horizontal displacement curves of test beam under different loads
2.3.3 裂缝开展形态分析
通过对试验过程中试验梁裂缝开展形态的观察发现: 裂缝开展初期阶段,由于叠合梁预制构件高度较小,存在剪应力超前现象,因此叠合梁L2裂缝相对于整浇梁L1较早出现;随着荷载的继续施加,叠合梁L2结构本身原有的应力与后期加载引起的应力有些相互叠加,有些相互抵减,此现象随着裂缝数量的增加和长度的延伸,使截面上的应力不断地发生重分布; 当裂缝在开展到接近叠合面附近时略有停滞,存在剪应力滞后现象,减缓了裂缝穿过叠合面的时间,使得前一阶段所施加的荷载对预制构件的影响进一步减弱,即梁上所有荷载逐步地由整个叠合梁L2截面来承受,从而提高了结构的整体承载力; 最后,叠合梁的整个变形形态也逐渐与整浇梁L1的变形形态接近,直至最终破坏。试验梁破坏形态如图12所示。

(b) 叠合梁破坏形态
此外,叠合梁裂缝开展到叠合面时沿叠合面方向存在微小滑移现象,根据试验过程中的观察以及对测定数据的分析,可知其产生原因可能有以下2点: 一是混凝土强度偏低,进而造成叠合面剪力槽在荷载作用下发生了局部破损,降低了其抗剪能力;二是由于叠合面剪力槽深度相对于叠合结构厚度偏小,随着荷载的增加,剪力槽已不能抵抗结构变形,最终导致滑移的产生。
3 结论与讨论
针对目前地下工程中叠合结构存在的接触面预处理施工难度大、工期长,剪力槽设置参差不齐等难题,提出一种便于施工的新型叠合结构形式,并运用ANSYS有限元软件以及开展现场静力荷载试验对其进行受力分析,得到以下结论。
1)通过运用ANSYS有限元软件对波浪形、三角形以及梯形波纹叠合面进行受力分析,得出梯形叠合面模型受力更加明确、合理,应力集中区域较少,最大滑移量仅为1.791×10-3mm,明显优于波浪形叠合面的2.84×10-3mm以及三角形叠合面的2.628×10-3mm。
2)现场静力荷载试验表明,叠合梁与整体现浇梁在受到相同荷载作用下,叠合梁挠度变形量反而优于整体现浇梁,这与叠合面两侧所配置的钢筋承受了一部分的荷载、抑制了梁的弯曲变形作用有很大关系; 同时,叠合梁在裂缝开展至叠合面时存在停滞现象,减缓了裂缝穿过叠合面,从而提高了结构的整体承载力。
3)叠合梁在裂缝开展至叠合面时,沿叠合面产生了水平向的微小滑移,其产生原因可能与混凝土强度以及剪力槽深度存在一定关系,此影响因素有待后续进行更加深入的研究。

