双线地铁隧道泥水及土压平衡盾构施工地层变形特征研究

吴红博， 周传波， 蒋 楠， 高 坛

(中国地质大学(武汉)工程学院， 湖北 武汉 430074)

0 引言

近年来随着城市的发展，地面交通越来越拥挤，各大城市通过兴建地铁缓解交通压力。地铁隧道开挖会引起不同程度的地层变形，地层变形较大时会造成地表路面塌陷、破坏地下埋设的管线、危及邻近建筑物安全。因此，在复杂的地层条件下，选择合适类型的盾构和合理的施工参数进行施工对地层变形控制十分重要。

关于盾构施工引起地层变形，国内外学者做了大量研究。R. B. Peck[1]认为隧道施工引起的地表沉降曲线符合正态分布。此后，一些学者从理论分析[2]、数值模拟[3-4]等方面做了研究工作。魏新江等[5]根据现场监测数据对地层位移规律与盾构参数关系进行了研究。姜忻良等[6]将实测数据与数值模拟相结合，对盾构施工地层水平位移和深层沉降进行了研究。王忠昶等[7]运用有限元软件对双线隧道盾构施工进行数值模拟分析，得到不同深度的地层位移规律。蒋胜光等[8]利用有限元软件对圆砾地层双线盾构施工参数与地表沉降规律进行了数值模拟研究。林存刚等[9]通过对杭州庆春路双线隧道采用泥水平衡盾构穿越大堤的实测数据进行研究，探讨了盾构掘进参数与地面沉降的关系。李承辉等[10]以兰州地铁1 号线迎门滩站—马滩站区间双线隧道采用泥水平衡盾构施工为背景，分析左右线盾构通过时地层深层沉降监测数据，研究了泥水平衡盾构对砂卵石地层的扰动状态。杨晓华[11]依托兰州某区间地铁隧道工程，利用数值模拟研究了砂卵石地层中双线采用土压平衡盾构引起的地层变形规律。王国富等[12]以兰州轨道交通1号线某区间试验段为工程案例，对现场监测数据进行分析，得出泥水平衡盾构控制沉降优于土压平衡盾构。

综上所述，目前对双线地铁隧道采用不同类型盾构施工引起地层变形规律的研究较少。本文以南宁地铁3号线东葛路站—滨湖路站区间双线隧道分别采用泥水平衡盾构和土压平衡盾构施工为背景，利用现场监测数据与数值模拟相结合的方法分析2种类型盾构在圆砾地层施工时引起的地层变形规律，以期为该地区类似地质条件下的盾构选型和安全施工提供参考。

1 工程概况

南宁市地铁3号线东葛路站—滨湖路站区间采用盾构法施工，区间全长957 m。隧道主要穿越圆砾层、粉质黏土层，局部穿越粉土层、粉砂层。区间稳定水位埋深为8.90～12.50 m，高程为63.20～67.42 m，承压水位埋深为10.40 m，隧道顶埋深约为11.7～21.0 m，区间线路线间距为8.0～14.0 m。东葛路站—滨湖路站区间线路纵坡为“V”形坡，左线最大坡度为28.167‰，右线最大坡度为27.537‰。地层纵向剖面如图1所示，土层的主要物理参数见表1。

区间左线泥水平衡盾构先行，右线土压平衡盾构后行。其中左线采用气垫式泥水平衡盾构，盾构刀盘直径为6 280 mm，刀盘开口率为35%，刀具由5把滚刀、27把先行撕裂刀、46把刮刀、8把贝壳刀、4把边缘保护刀组成。主机的外形尺寸为： 前盾直径6 250 mm,中盾直径6 240 mm，盾尾直径6 230 mm，机身长8 700 mm，盾尾间隙为75 mm。土压平衡盾构刀盘直径为6 280 mm，刀盘开口率为30%，刀具由1把仿形刀、 28把滚刀、 16把刮刀、8把重型撕裂刀、64把齿刀组成。主机的外形尺寸为： 前盾直径6 250 mm,中盾直径6 240 mm，盾尾直径6 240 mm，机身长8 300 mm，盾尾间隙为75 mm。2台盾构由盾尾注浆管进行同步注浆，注浆管路为4个。管片外径D1=6.0 m，管片内径D2=5.4 m，环宽1.5 m，混凝土强度等级为C50。

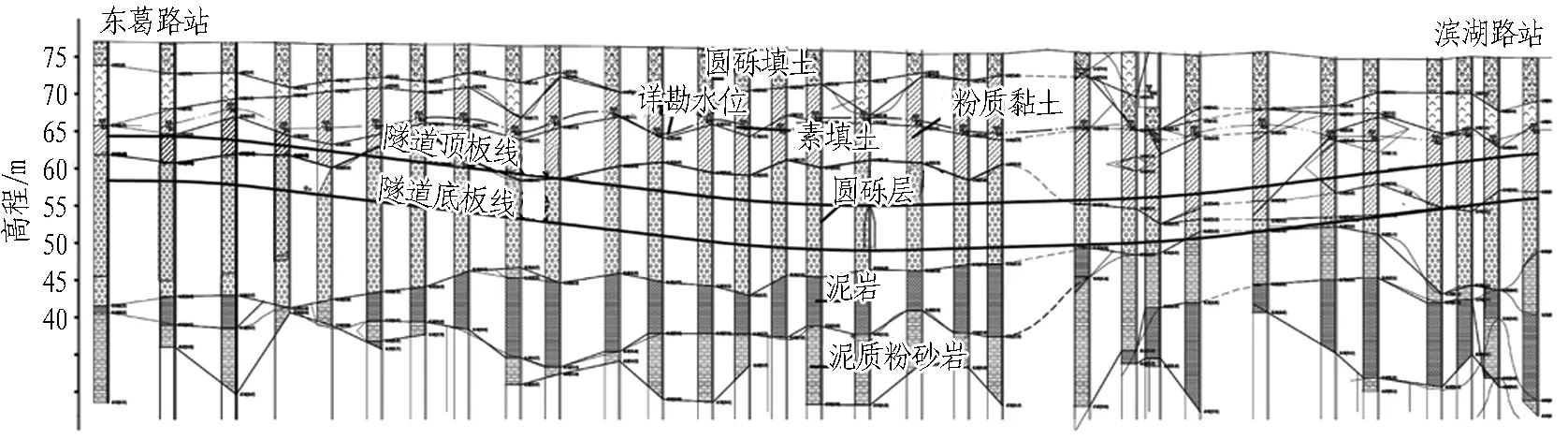
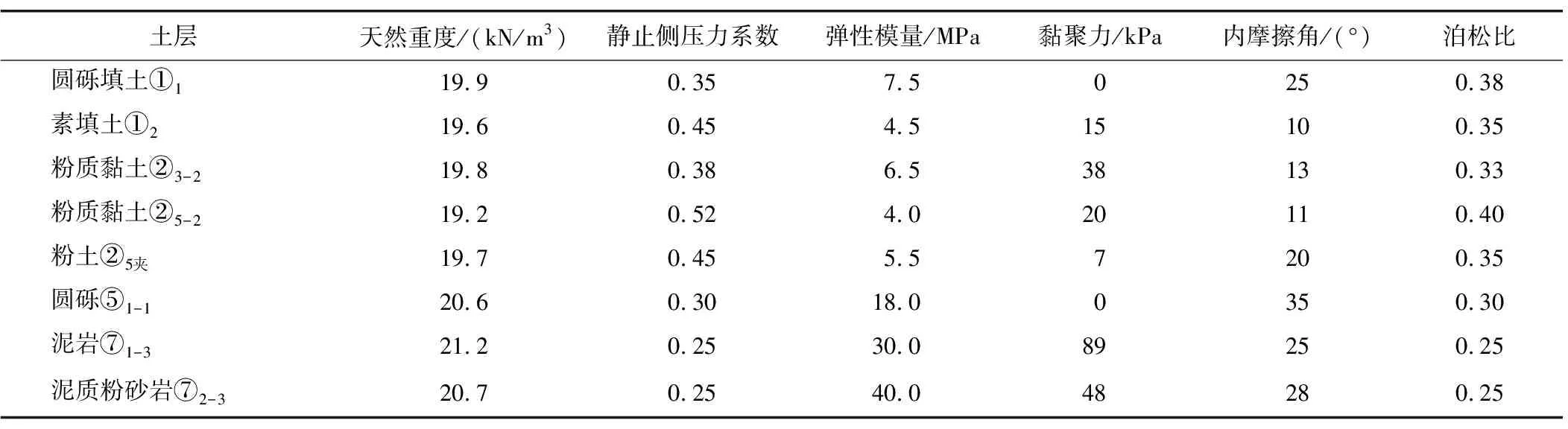
图1 地层纵剖面图

2 地表变形实测数据分析

在隧道盾构施工过程中，地表沉降监测数据可以直观地反映盾构施工造成的地层损失。

2.1 地表沉降监测布置

隧道在圆砾地层区段的监测点布置如图2和图3所示，每30 m布设一个横向监测断面，隧道轴线正上方每10 m布置一个地表沉降监测点。区间其他部分的沉降监测与图2和图3类似。

2.2 盾构施工变形特征实测分析

本文针对2种类型盾构在圆砾地层施工，对典型监测断面DB26和隧道轴线正上方监测点的现场监测数据进行统计分析。

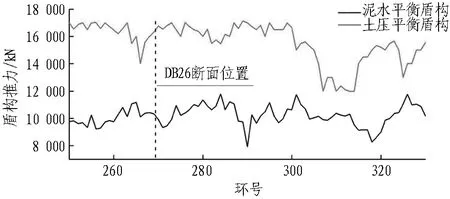
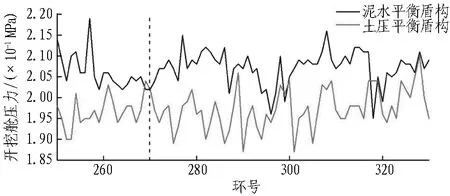
图4示出2台盾构穿越DB26断面前后的掘进参数。由图4可知： 此区段泥水平衡盾构推力、刀盘转矩小于土压平衡盾构，掘进速度、开挖舱压力略大于土压平衡盾构。泥水平衡盾构推力为7 900～12 000 kN，土压平衡盾构推力为12 000～17 000 kN；泥水平衡盾构刀盘转矩为300～700 kN·m，土压平衡盾构刀盘转矩为900～1 700 kN·m； 泥水平衡盾构掘进速度在35 mm/min左右，土压平衡盾构掘进速度在28 mm/min左右； 2台盾构开挖舱压力均在0.2 MPa左右，同步注浆量均为5～7.5 m3，注浆压力均为0.2～0.35 MPa。

图2监测点平面布置图

Fig. 2 Layout of monitoring points

图3 监测点横断面布置及地层分布图(单位： m)

Fig. 3 Cross-section of layout of monitoring points and strata distribution (unit： m)

(a) 盾构推力

(b) 刀盘转矩

(c) 掘进速度

(d) 开挖舱压力

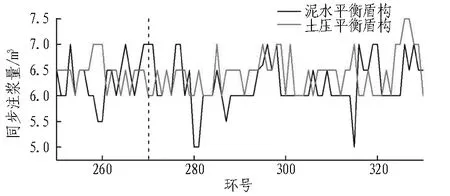
(e) 同步注浆量

(f) 注浆压力

图4盾构穿越DB26断面前后掘进参数

Fig. 4 Tunneling parameters of shield before and after crossing cross-section DB26

图5示出隧道穿越圆砾地层时地表典型断面DB26的实测沉降曲线。由图5可知： 左线隧道泥水平衡盾构通过时，地表最大沉降量为5.5 mm，隧道轴线两侧8.0 m范围外地表无明显沉降； 右线隧道土压平衡盾构通过时，地表最大沉降量为18.7 mm，隧道轴线两侧18.0 m范围外地表无明显沉降； 双线隧道掘进完成后，地表最大沉降量为21.59 mm。土压平衡盾构开挖造成的地表沉降量以及影响范围明显大于泥水平衡盾构。

图5 DB26断面地表沉降曲线

图6和图7分别示出泥水平衡盾构和土压平衡盾构通过监测点前后监测点的沉降历程曲线(其中隧道轴线上方Z66、Z65、Z64、Z61、Z60、Y66、Y65、Y64、Y61、Y60监测点数据完整)。由图6和图7可知： 1)2种类型盾构刀盘到达距监测点3D1位置前监测点未产生沉降(隆起)； 2)盾构到达距监测点2D1左右位置时，监测点开始沉降(隆起)，直到盾体通过监测点所在区段，监测点沉降量较小； 3)盾构盾尾通过监测点后，监测点沉降量迅速增加，泥水平衡盾构盾尾通过距监测点约2D1位置时沉降量达到峰值，土压平衡盾构盾尾通过距监测点约3D1位置时沉降量达到峰值。2种盾构在圆砾地层施工时，土压平衡盾构与泥水平衡盾构相比，盾尾脱离管片时监测点产生较大沉降，导致最终地面沉降量较大。

3 双线隧道盾构掘进过程的数值模拟

本文采用FLAC3D软件进行数值模拟分析，依据现场监测数据的规律，对数值模拟进行以下简化： 2种类型盾构盾尾脱离管片时采用不同的应力释放程度来模拟周围土体扰动和非及时注浆所导致的地层变形。

3.1 数值模型的建立

模型上边界按实际覆土分层取至地表，隧道埋深18 m，向下取至隧道底部以下21 m，横向取隧道外侧29.5 m,双线平行隧道轴线间距为11 m，沿纵向取72 m，由此建立FLAC3D三维数值模型的尺寸为72 m×81 m×45 m(长×宽×高)。边界条件为： 上表面边界为自由边界，侧面边界限制水平方向位移，底部边界限制竖向位移。盾壳和衬砌管片采用壳单元，土体和注浆层采用实体单元。建立三维数值模型，如图8所示。

图6 泥水平衡盾构施工引起的监测点沉降历程曲线

Fig. 6 Time-history settlement curves of monitoring points induced by slurry balance shield construction

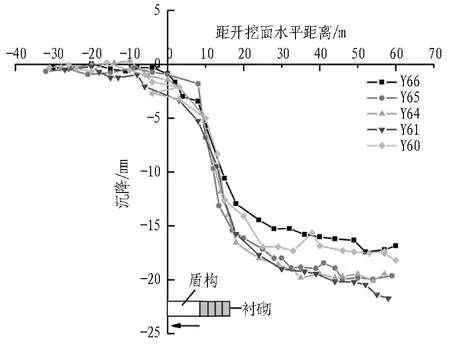
图7 土压平衡盾构施工引起的监测点沉降历程曲线

Fig. 7 Time-history settlement curves of monitoring points induced by EPB shield construction

图8 FLAC3D数值模型

3.2 本构模型和材料的力学参数

本文土体采用摩尔-库仑(Mohr-Coulomb)弹塑性模型，盾壳、衬砌管片和注浆层采用弹性材料，地层材料参数采用勘察资料取值。模型计算采用的力学参数见表2。

表2 模型材料力学参数

3.3 盾构施工模拟步骤和模拟方案设计

在自重应力下，模型运算至平衡后计算土体的初始应力场，产生的位移清零。具体步骤如下：

1)沿隧道开挖方向开挖9.0 m(约盾体长度)，隧道内壁施加盾构钢壳，在掌子面施加0.2 MPa(开挖舱压力)的均布荷载，运行至平衡，以模拟盾构进入土体。

2)盾构每个循环向前掘进3.0 m(2个管片长度)，在距离开挖面9.0 m处去除盾构钢壳，计算一定时步，使周边土体产生变形，以模拟盾尾空隙和注浆不及时造成的地层变形。

3)安装管片，施加注浆层，根据现场注浆参数施加0.25 MPa的注浆压力； 先开挖左线隧道，后开挖右线隧道。

依据现场监测数据中2台盾构盾尾脱离管片后的地表沉降差异，2台盾构盾尾脱离管片时采用不同的计算时步使地层发生变形。图9和图10分别示出实际工况下双线隧道掘进完成时的竖向位移和轴线方向Y=36 m处地表沉降曲线。由图10可知，数值模拟得到的结果与实测值相比，沉降槽宽度和深度基本一致，验证了数值模拟方法的可行性。本文设计模拟3种工况，工况1(实际工况)： 双线隧道左线采用泥水平衡盾构施工，右线采用土压平衡盾构施工。工况2： 双线隧道均采用泥水平衡盾构施工。工况3： 双线隧道均采用土压平衡盾构施工。

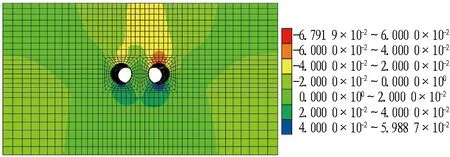
图9 竖向位移云图(单位： m)

4 数值模拟结果分析

4.1 双线隧道盾构施工引起地层沉降特征分析

图11示出工况1下双线隧道掘进完成时隧道轴线方向Y=36 m处不同深度地层的沉降曲线。由图11可知： 随着地层深度的增加，右线隧道上方地层沉降越来越大，而左线隧道上方地层沉降无明显增加。其中，在地表X=0 m处沉降量为13.7 mm，X=11 m处沉降量为20 mm； 在埋深6.5 m粉质黏土层X=0 m处沉降量为14 mm，X=11 m处沉降量为21 mm； 在埋深12 m软塑状粉质黏土层X=0 m处沉降量为14.2 mm，X=11 m处沉降量为26.5 mm； 在埋深16 m圆砾层X=0 m处沉降量为17 mm，X=11 m处沉降量为44.5 mm。双线隧道掘进完成时，地层沉降槽曲线偏向右线隧道。

图10 双线隧道掘进完成时Y=36 m处地表沉降曲线

Fig. 10 Surface settlement curve atY=36 m when two lines are completed

图12和图13分别示出工况2和工况3下双线隧道掘进完成时隧道轴线方向Y=36 m处不同深度地层的沉降曲线。由图12和图13可知： 1)双线隧道掘进完成时，不同工况下引起的不同深度地层最大沉降见表3，双线隧道采用土压平衡盾构施工地层沉降较大，更可能危及周边建筑物及基础的安全； 2)随着地层深度的增加，单线隧道开挖沉降槽越来越窄，双线隧道掘进完成后地层沉降曲线呈“W”形状越来越明显，在深度16 m的圆砾地层和深度12 m的软塑状粉质黏土层,沉降曲线呈“W”形状； 3)地层距离地表越近，沉降影响范围越大，其中工况2下双线隧道采用泥水平衡盾构掘进时，地表沉降影响范围约30 m； 工况3下双线隧道采用土压平衡盾构掘进时，地表沉降影响范围约50 m。

Fig. 11 Ground settlement curves at different depths atY=36 m in condition 1

图12工况2下Y=36 m处不同深度地层沉降曲线

Fig. 12 Strata settlement curves at different depths atY=36 m in condition 2

图13 工况3下Y=36 m处不同深度地层沉降曲线

Fig. 13 Strata settlement curves at different depths atY=36 m in condition 3

表3不同工况下引起的地层最大沉降

Table 3 Maximum settlement of strata caused by different working conditions

埋深/m最大沉降量/mm工况2工况308.6306.59.432.91211.334.71616.546

4.2 双线隧道盾构施工引起地表水平变形特征分析

地铁隧道盾构施工引起的地表水平位移危及埋设近地表管线的安全。本文对不同工况下地表水平位移规律进行分析，以期为安全施工提供参考。

图14示出工况1下单线掘进完成和双线掘进完成时隧道轴线方向Y=36 m处地表水平位移曲线。由图14可知： 单线(左线)隧道掘进完成时地表水平位移曲线以左线隧道轴线对称分布，双线隧道掘进完成时地表水平位移曲线呈非对称性。双线隧道掘进完成后最大水平位移发生在X=-3 m位置，为6.4 mm，地表水平位移向右线隧道轴线移动。工况1下，土压平衡盾构施工引起的水平变形是总水平变形的主要部分。

图14 工况1下Y=36 m处地表水平位移曲线

Fig. 14 Horizontal surface displacement curves atY=36 m in condition 1

图15和图16分别示出工况2和工况3下单线掘进完成和双线掘进完成时隧道轴线方向Y=36 m处地表水平位移曲线。由图15和图16可知： 单线(左线)隧道掘进完成时地表水平位移曲线以左线隧道轴线对称分布，双线隧道掘进完成时地表水平位移曲线以双线隧道中线对称分布。在工况2下，单线(左线)隧道掘进完成时在X= 9.0 m位置处水平位移达到最大，为2.4 mm； 双线隧道掘进完成时，最大位移量约为3.0 mm，在距离双线隧道中线10.0 m位置处。在工况3下，单线(左线)隧道掘进完成时在X=10.0 m位置处水平位移达到最大，为6.0 mm； 双线隧道掘进完成时，地表水平位移最大值为9.4 mm，在距离双线隧道中线13.0 m处。双线隧道先后施工时，双线隧道轴线间地表出现不同方向位移，土压平衡盾构施工造成的地表水平位移量大，对埋设近地表管线有较为明显的剪切作用。

图15 工况2下Y=36 m处地表水平位移曲线

Fig. 15 Horizontal surface displacement curves atY=36 m in condition 2

图16 工况3下Y=36 m处地表水平位移曲线

Fig. 16 Horizontal surface displacement curves atY=36 m in condition 3

5 结论与建议

本文基于现场监测数据和数值模拟对土压平衡盾构和泥水平衡盾构在圆砾地层施工的变形特征进行分析，得到以下结论。

1)在圆砾地层盾构施工时，土压平衡盾构施工造成的地面沉降量和沉降范围大于泥水平衡盾构。

2)土压平衡盾构与泥水平衡盾构相比，盾尾通过测点后有较大的沉降。土压平衡盾构盾尾通过距监测点3D1位置后地层趋于平稳，泥水平衡盾构盾尾通过距监测点2D1位置后地层趋于平稳。

3)双线隧道采用2种类型盾构施工时，地层沉降槽曲线偏向土压平衡盾构施工的隧道； 双线隧道采用同种盾构掘进完成时，深度越大的地层，其沉降曲线呈“W”形状越明显； 双线隧道全部采用土压平衡盾构施工，地层发生较大的沉降，地表沉降影响范围约为50 m，而采用泥水平衡盾构施工的地表影响范围为30 m。

4)双线隧道采用2种类型盾构施工时，地表水平变形主要是由土压平衡盾构施工引起； 双线隧道采用同种盾构施工时，单线隧道掘进完成时地表水平位移曲线以隧道轴线对称分布，双线隧道掘进完成时地表水平位移曲线以双线隧道中线对称分布。双线隧道先后施工时，双线隧道轴线之间地表出现不同方向水平位移，土压平衡盾构施工引起的地表水平位移更大，对此范围内埋设的近地表管线有较为明显的剪切作用。

本文采用现场实测和数值模拟计算相结合的方法，研究了泥水及土压平衡盾构施工双线隧道的地层变形规律。但是，数值模拟时依据现场监测点变形历程特征对2种盾构进行了简化，对2种类型盾构的精细化模拟以及盾构不同施工顺序产生的影响还有待进一步研究。